本文主要是介绍838. 堆排序,,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
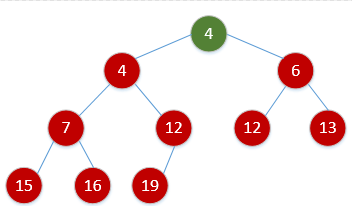
完全二叉树手写小根堆
堆排序的五大功能
1.插入一个数
2.求集合当中的最小值
3.删除最小值
4.删除任意一个元素
5.修改任意一个元素
(最后两个功能stl中的堆即优先队列都没法直接实现)
输入一个长度为 n 的整数数列,从小到大输出前 m 小的数。
输入格式
第一行包含整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
输出格式
共一行,包含 m 个整数,表示整数数列中前 m 小的数。
数据范围
1≤m≤n≤105,
1≤数列中元素≤109
输入样例:
5 3
4 5 1 3 2
输出样例:
1 2 3解析:
此代码的第一次排序时间复杂的为 O(n)
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>using namespace std;
typedef long long LL;
const int N = 1e5 + 5, M = 3e5 + 5;
int n, m;
int h[N],cnt;void down(int u) {int t = u;if (u * 2 <= cnt && h[2 * u] < h[t])t = 2 * u;if (2 * u + 1 <= cnt && h[2 * u + 1] < h[t])t = 2 * u + 1;if (u != t) {swap(h[t], h[u]);down(t);}
}int main() {cin >> n >> m;for (int i = 1; i <= n; i++)scanf("%d", &h[i]);cnt = n;for (int i = n / 2; i; i--)down(i);//时间复杂度为 O(n)while (m--) {printf("%d ", h[1]);h[1] = h[cnt];cnt--;down(1);}return 0;
}这篇关于838. 堆排序,的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!