kr 第三阶段（五）32 位逆向

本文主要是介绍kr 第三阶段（五）32 位逆向，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

如何寻找 main 函数

• 对于低版本的 VC 编译器（VC 6.0），main 函数在 PE 入口点 mainCRTStartup 函数中是倒数第 3 个函数调用，且参数个数为 3 个（wmain 函数为 4 个参数）。

• 对于高版本的 VC 编译器

  • 程序入口点 mainCRTStartup 函数调用了一个 __scrt_common_main 函数。release 版程序的 __scrt_common_main 函数会被内联到 mainCRTStartup 函数中。
  • __scrt_common_main 函数调用 __security_init_cookie 函数和 __scrt_common_main_seh 两个函数。前一个函数是初始化 cookie ，在 GS 保护时会用到。后一个函数是调用 main 函数的关键函数（release 版会优化为一个 jmp）。
  • __scrt_common_main_seh 函数会调用 invoke_main 函数，invoke_main 函数会调用 main 函数。定位 invoke_main 函数可以找 __scrt_common_main_seh 函数末尾连续两个 if 判断之后立即调用且没有参数的函数。如果是 release 版程序由于 invoke_main 函数被内联因此直接在函数末尾找 3 个参数的函数调用即可。

• 如果是其他编译器可以先编译一个程序调试查看函数调用堆栈寻找定位特征。

• IDA 内置常见库的签名文件，因此一般能够通过代码特征识别出 main 函数。

制作 IDA 签名文件

以 VC 6.0 为例，之前安装目录下的 VC98\Lib 中有很多 lib 库，其中有一组前缀为 LIBC 的 libc 库中存放着很多库函数。这些 libc 库的后缀有如下含义：

• I：导入版（没有具体实现，只是引入动态链接库）
• D：调试版
• MT：多线程
• P：C++

这里根据逆向分析的程序特征分析出所使用的 lib 库为 LIBC.lib 。

LIBC.lib 实际上是由多个 obj 类型的文件组成。每个 obj 文件对应一个库函数。在链接时，链接器从中递归查找所需要的库函数链接进代码中，从而避免将多余的代码链接进程序中。我们使用 VC 6.0 自带的链接器可以查看 LIBC.lib 中的 obj 文件。

> link -lib /list .\LIBC.LIB
Microsoft (R) Library Manager Version 6.00.8168
Copyright (C) Microsoft Corp 1992-1998. All rights reserved...\build\intel\st_obj\util.obj
..\build\intel\st_obj\matherr.obj
..\build\intel\st_obj\ldexp.obj
..\build\intel\st_obj\ieeemisc.obj
..\build\intel\st_obj\frexp.obj
..\build\intel\st_obj\fpexcept.obj
..\build\intel\st_obj\bessel.obj
...

另外我们还可以将其中某个特定的 obj 文件提取出来。

link -lib /extract:build\intel\st_obj\printf.obj .\LIBC.LIB

提取出 obj 文件后，有一个 Flair 的工具可以制作签名文件。

首先使用 pcf （ELF 文件使用 pelf）从 printf.obj 中提取特征，得到 printf.pat 文件。

pcf .\printf.obj

之后使用 sigmake 将提取的特征文件 printf.pat 制作成 IDA 的签名文件 printf.sig 。这里 -n 用来添加备注。

sigmake -n"TestSig" .\printf.pat printf.sig

对于 IDA 7.7 需要将签名文件放到其安装目录下 sig 文件夹下的具体文件夹中，这里我放在 pc 文件夹中。之后再 IDA 中使用快捷键 Shift + F5 打开签名窗口右键添加签名文件。

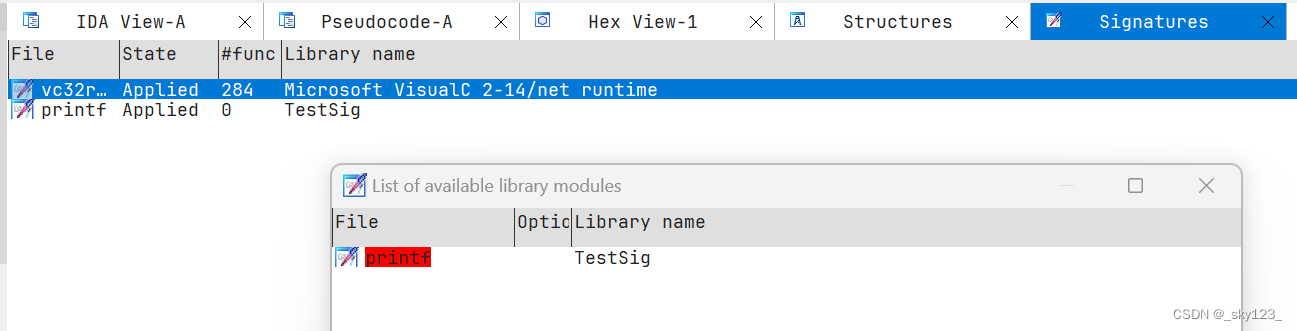
此时 printf 函数被识别出来并且 printf 函数所在位置被 IDA 标记为浅蓝色，表示 IDA 将这段代码其标记为库函数代码。

上面只是添加了一个函数的签名文件，实际我们可以使用 lib2sig.bat 脚本将制作签名的过程自动化。

md %1_objs
cd %1_objs
for /f %%i in ('link -lib /list %1.lib') do link -lib /extract:%%i %1.lib
for %%i in (*.obj) do pcf %%i
sigmake -n"%1.lib" *.pat %1.sig
if exist %1.exc for %%i in (%1.exc) do find /v ";" %%i > abc.exc
if exist %1.exc for %%i in (%1.exc) do > abc.exc more +2 "%%i"
copy abc.exc %1.exc
del abc.exc
sigmake -n"%1.lib" *.pat %1.sig
copy %1.sig ..\%1.sig
cd ..
del %1_objs /s /q
rd %1_objs

使用如下命令就可以制作出 LIBC.LIB 的签名文件 LIBC.sig 。注意脚本中使用的 lib 名为小写，因此需要手动修改 lib 库的名称为 LIBC.lib 。

.\lib2sig.bat LIBC

然而 LIBC.lib 中有部分 16 位的 obj 文件 pcf 无法处理且 pcf 退出之前会用 getchar 阻塞，因此脚本会被卡住。需要将 pcf 脱壳之后 patch 掉 getchar 解决。

> pcf nset.obj
nset.obj is not ar/coff filepress enter to exit.

表达式

基本概念

表达式的类型

运算的表达式类型分为波兰表达式，中缀表达式，逆波兰表达式。以 $a+b\times c-d/f$ 为例，该表达式可以转换为如下表达式树：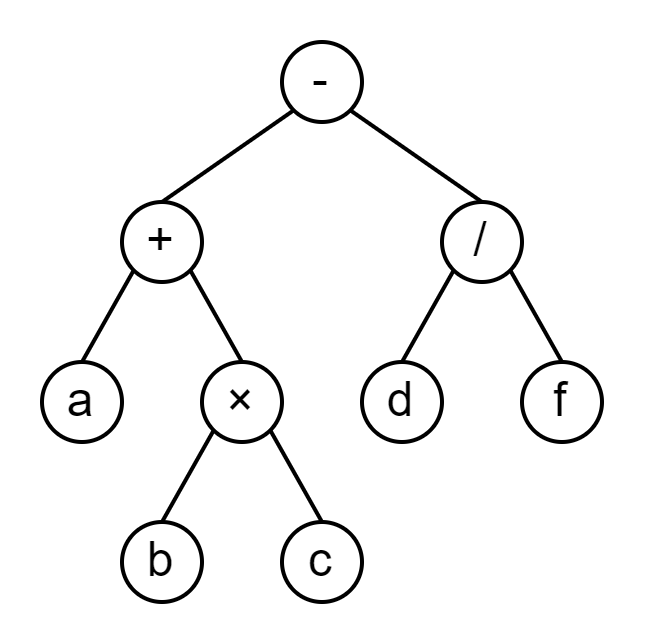
而三种表达式对应于该树的三种遍历方式：

• 波兰表达式：前序遍历，$-+a\times bc/df$。
• 中缀表达式：中序遍历，$a+b\times c-d/f$。
• 逆波兰表达式：后续遍历，$abc\times +df/-$ 。

在表达式树中值一定在叶子节点而运算符一定不在叶子节点。因为波兰表达式和逆波兰表达式可以确定直接与一个运算符相连的两个叶子节点，从而确定出表达式的运算顺序，而中缀表达式需要额外提供运算优先级信息才能还原出运算顺序，因此计算机通常采用波兰表达式来表示一个表达式。比如上面的例子写为函数调用形式是 sub(add(a, mul(b, c)), div(d, f))，这就是一个波兰表达式。

大多数编译器会将各种运算的表达式转换为波兰表达式。

表达式的优化

• 运算必须传回结果的值，否则不产生任何代码。常见传值有三种方式：赋值运算，函数传参和返回值。
• 如果运算表达式的中的值都是常量会触发常量折叠，即用表达式的运算结果代替表达式。当然如果表达式中的值不都是常也会有常量折叠，例如 3 * n + 6 * n 可以被优化为 9 * n 。
• Release 版程序针对表达式还会有窥孔优化，即使用各种优化方案在某个局部代码处，如果能成功使用则重新扫描并再次尝试优化，如果各方案都不能使用则优化结束。
• 另外 Release 版程序针对表达式还会有常量传播优化，即如果表达式其中一个值为变量，而这个变量的值可以推算出是确定的值，则将表达式中对应的值替换为常量。可以与常量折叠配合使用。
• 复写传播：类似常量传播，只不过传播的是变量而不是常量。例如 x = x + 8; x = x + 8; 优化为 x = (x + 8) + 8 即 x = x + 16 。
• 强度削弱：使用的代价的指令序列来替换高代价的指令序列。例如使用 lea 和移位指令替换乘法和除法指令。

取整

取整有三种类型：

• 向上取整：$\lceil \frac{a}{b}\rceil$
• 向下取整：$\lfloor \frac{a}{b}\rfloor$
• 向零取整：$\left[\frac{a}{b}\right]$

C/C++ 以及绝大多数变成语言都采用向零取整的策略（当然也有一些例外，例如 python 是向下取整）。

除法

• 除数为变量时无法优化，根据除数类型选择 div 或 idiv 。
• 除数为常量时可以优化。

被除数无符号，除数为 2 的整数次幂

直接 shr 移位即可。

被除数有符号，除数为 2 的整数次幂

如果被除数有符号除数为 2 的整数次幂那么会转换为算术移位操作。但是如果被除数为负数需要做特殊处理。

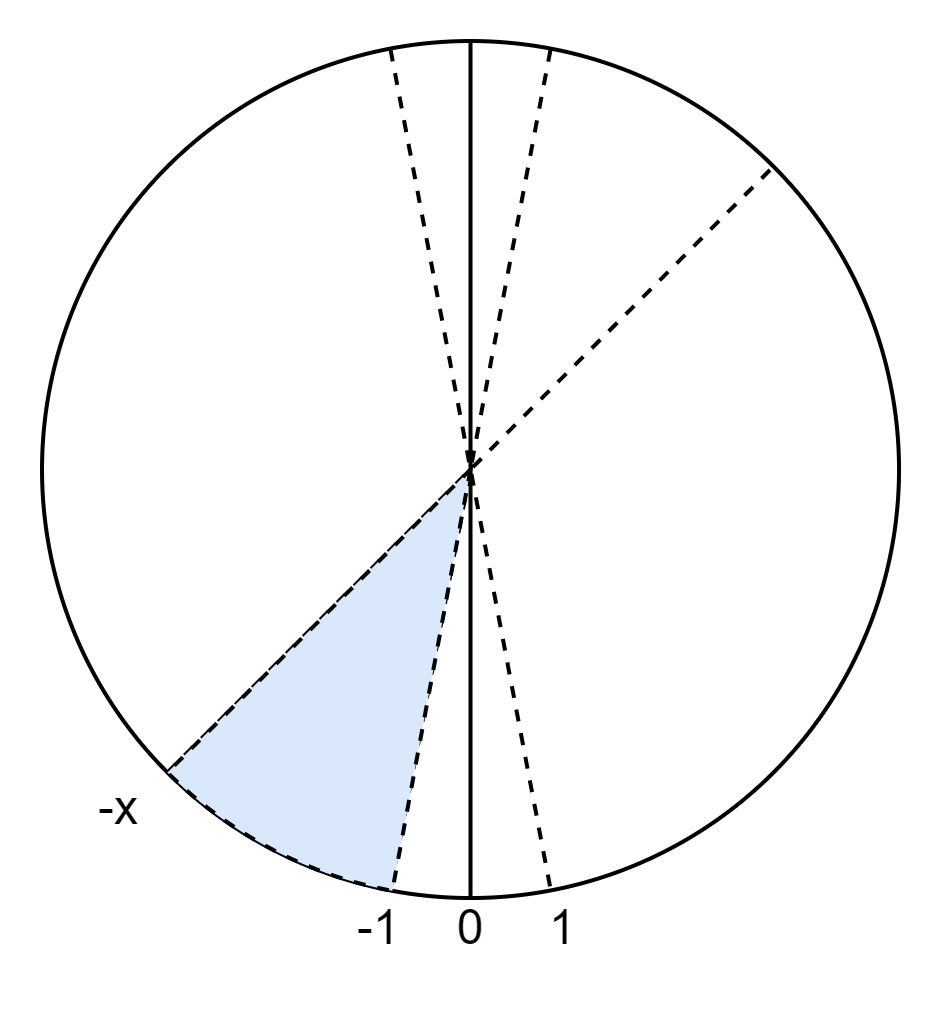
首先对于一个负数 $-x$，如果是进行算术右移 $n$ 位，高位会补符号位。实际上这个右移的过程我们可以看做是上图中蓝色的部分右移的过程，也就是说右移完之后 $-x$ 变成了 $-\lfloor \frac{x-1}{2^n}\rfloor -1=-\lfloor \frac{x+2^n-1}{2^n}\rfloor =-\lceil \frac{x}{2^n}\rceil$ 。

然而我们期望得到的结果是 $\left[\frac{-x}{2^n}\right]=-\lfloor \frac{x}{2^n}\rfloor$ 。

因此我们可以在右移前在分子上加上 $2^n-1$ ，也就是上图蓝色的部分减少 $2^n-1$ 。

因此原式变为 $-\lfloor \frac{x-1-(2^n-1)}{2^n}\rfloor -1=-\lfloor \frac{x}{2^n}\rfloor =\left[\frac{-x}{2^n}\right]$ 。

例如 x / 8 可以优化为如下汇编代码：

mov eax, x
cdq
and edx, 7
add eax, edx
sar eax, 3

• cdq 指令的作用是取 eax 的最高位填充到 edx 中，即如果 i < 0 则 edx = 0xFFFFFFFF，否则 edx = 0 。
• 如果除数为负数，由于向零取整的特性会把符号提出类。对应到汇编代码中是正常优化后再最后结果用 neg 指令取负数。

特别的，如果除数为 2 需要被除数加 1 ，因此直接被除数减去 edx 即可。

mov eax, x
cdq
sub eax, edx
sar eax, 1

被除数无符号，除数为非 2 的整数次幂

对于被除数无符号除数为非 2 的整数次幂的情况，为了避免使用除法指令，可以做如下转换：
$$\lfloor \frac{a}{b}\rfloor =\lfloor \frac{a\times \lceil \frac{2^n}{b}\rceil }{2^n}\rfloor (n\ge \lceil {\log }_{2}a\rceil )$$
关于上式证明如下：

不妨设
$$2^n=b\times k+r(0<r<b,k\in \mathbb{N})$$
则
$$\frac{a\times \lceil \frac{2^n}{b}\rceil }{2^n}=\frac{a\times k+a}{b\times k+r}$$
若要使得源等式成立，则要满足
$$\frac{a}{b}\le \frac{a\times k+a}{b\times k+r}<\frac{a+b}{b}$$
首先显然有如下不等式成立：
$$\frac{a\times k+a}{b\times k+r}>\frac{a\times k+a}{b\times k+b}$$
由于 $k\in \mathbb{N}$ ，因此
$$\frac{a\times k+a}{b\times k+r}>\frac{a}{b}$$
而不等式
$$\frac{a\times k+a}{b\times k+r}<\frac{a+b}{b}$$
等价为
$$b\times (2^n-a)+a\times r>0$$
显然也成立。

综上，原命题得证。

对于 32 位程序，这里的 $n$ 的值要比 32 大，因此会用到 eax 和 edx 编译器。例如$\lfloor \frac{a}{23}\rfloor$对应的汇编代码如下：

.text:00401000 mov     eax, 0B21642C9h
.text:00401005 mul     [esp+a]
.text:00401009 shr     edx, 4
.text:0040100C push    edx

这里 0B21642C9h 即$\lceil \frac{2^{36}}{23}\rceil$，我们称之为 MagicNumber。由于运算结果大小超过 32 位，因此使用 edx 寄存器存储高 32 位，这就是为什么后面要将 edx 右移 4 位。

特别的，如果除数特别小时会出现 MagicNumber 也超过 32 位的情况。 例如$\lfloor \frac{a}{7}\rfloor$优化后为$\lfloor \frac{a\times \lceil \frac{2^{35}}{7}\rceil }{2^{35}}\rfloor$然而$\lceil \frac{2^{35}}{7}\rceil$ 的值为 124924925h 大于 $2^{32}$因此有如下转换：
$$\lfloor \frac{a\times \lceil \frac{2^{35}}{7}\rceil }{2^{35}}\rfloor =\lfloor \frac{\frac{a-\lfloor \frac{a\times (\lceil \frac{2^{35}}{7}\rceil -2^{32})}{2^{32}}\rfloor }{2}+\lfloor \frac{a\times (\lceil \frac{2^{35}}{7}\rceil -2^{32})}{2^{32}}\rfloor }{2^2}\rfloor$$
具体推导如下：

首先
$$\lfloor \frac{a\times (\lceil \frac{2^{35}}{7}\rceil -2^{32})}{2^{32}}\rfloor =\lfloor \frac{a\times \lceil \frac{2^{35}}{7}\rceil }{2^{32}}\rfloor -a$$
因此
$$\begin{array}{rl}\lfloor \frac{\frac{a-\lfloor \frac{a\times (\lceil \frac{2^{35}}{7}\rceil -2^{32})}{2^{32}}\rfloor }{2}+\lfloor \frac{a\times (\lceil \frac{2^{35}}{7}\rceil -2^{32})}{2^{32}}\rfloor }{2^2}\rfloor & =\lfloor \frac{\frac{2\times a-\lfloor \frac{a\times \lceil \frac{2^{35}}{7}\rceil }{2^{32}}\rfloor }{2}+\lfloor \frac{a\times \lceil \frac{2^{35}}{7}\rceil }{2^{32}}\rfloor -a}{2^2}\rfloor \\ & =\lfloor \frac{\lfloor \frac{a\times \lceil \frac{2^{35}}{7}\rceil }{2^{32}}\rfloor }{2^3}\rfloor \\ & =\lfloor \frac{a\times \lceil \frac{2^{35}}{7}\rceil }{2^{35}}\rfloor \end{array}$$
其中 $\lceil \frac{2^{35}}{7}\rceil -2^{32}<2^{32}$ ，因此整个表达式中参与运算的常量不会超过 $2^{32}$ 。

对应汇编代码如下：

.text:00401000 mov     ecx, [esp+a]
.text:00401004 mov     eax, 24924925h
.text:00401009 mul     ecx
.text:0040100B sub     ecx, edx
.text:0040100D shr     ecx, 1
.text:0040100F add     ecx, edx
.text:00401011 shr     ecx, 2
.text:00401014 push    ecx

被除数有符号，除数为非 2 的整数次幂

对于被除数为有符号数的情况，汇编代码如下：

.text:00401000 mov     ecx, [esp+a]
.text:00401004 mov     eax, 38E38E39h
.text:00401009 imul    ecx
.text:0040100B sar     edx, 1
.text:0040100D mov     eax, edx
.text:0040100F shr     eax, 31			; 取 (MagicNumber * a) >> 33 的符号位即除法运算结果
.text:00401012 add     edx, eax			; 如果结果为负数则需要将结果加上 1
.text:00401014 push    edx

分析汇编可知，前 4 行与无符号数操作相似，唯一的不同是移位指令换做是有符号数的移位指令。后面 3 行指令是被除数为有符号数时特有的操作，因为如果被除数为负数则需要将结果加上 1，原理与前面被除数有符号除数为 2 的整数次幂相同，只不过指令简单粗暴的在最后结果上加 1（需要保证被除数不能被除数整除）。编译器取巧的直接将被除数的符号位加到结果上。

然而这样计算的前提是被除数不能被除数整除，因为一旦整除，但实际上编译器通过设置 $\lceil \frac{2^n}{b}\rceil$ 中的 $n$ 使得在 $a$ 能取到的值的范围内这种情况不会发生。例如上面的例子中通过设置 $n=33$ 使得 MagicNumber 为奇数，这样 $a$ 至少为 $2^{33}$ 才能出现这种情况，但实际上 $a$ 取不到这么大的值。

另外，a / 7 的汇编代码如下，这里不同的是在乘完 MagicNumber 后结果还要再加上 a 。这是因为 92492493h 是负数，而为了保留 a 的符号乘法使用的是有符号乘法。但是这里 MagicNumber 需要是无符号数才有实际意义。因为 mov eax, 92492493h; imul ecx; 实际为 mov eax, -6DB6DB6Dh; imul ecx;，而 -6DB6DB6Dh = 92492493h - 100000000h，因此要想使得结果正确需要在 MagicNumber 上加上 100000000h，也就是在 MagicNumber * a 结果的高 32 位加上 a 。

.text:00401000 mov     ecx, [esp+a]
.text:00401004 mov     eax, 92492493h
.text:00401009 imul    ecx
.text:0040100B add     edx, ecx		; 加上 a * 100000000h
.text:0040100D sar     edx, 2
.text:00401010 mov     eax, edx
.text:00401012 shr     eax, 1Fh
.text:00401015 add     edx, eax		; 负数向上取整
.text:00401017 push    edx

进一步，如果是 a / -7 那么汇编代码如下。由于是向零取整，因此可以把符号拿到分子上，这样做的后果是原来的 -6DB6DB6Dh (92492493h - 100000000h) 变为了 6DB6DB6Dh (100000000h - 92492493h)。而 MagicNumber 需要被当做 -92492493h（这个数字不能用 32 位有符号数表示）看待，原来多减了 100000000h 现在变成少减了 100000000h 。

.text:00401001 mov     esi, [esp+a]
.text:00401005 mov     eax, 6DB6DB6Dh
.text:0040100A imul    esi
.text:0040100C sub     edx, esi		; 减去 a * 100000000h
.text:0040100E sar     edx, 2
.text:00401011 mov     eax, edx
.text:00401013 shr     eax, 1Fh
.text:00401016 add     edx, eax		; 负数向上取整
.text:00401018 push    edx

这里需要注意，上面的情况是应当将 MagicNumber 作为正数运算，但是看做有符号数之后 MagicNumber 变为负数导致的运算错误需要修正。如果 MagicNumber 本来就是要当做负数运算就不需要修正。例如下面的 a / 17 和 a / -17 ：

.text:00401001 mov     esi, [esp+a]
.text:00401005 mov     eax, 78787879h
.text:0040100A imul    esi
.text:0040100C sar     edx, 3
.text:0040100F mov     eax, edx
.text:00401011 shr     eax, 1Fh
.text:00401014 add     edx, eax
.text:00401016 push    edx
...
.text:00401021 mov     eax, -78787879h	; 将 -17 中的负号转移至 MagicNumber 上
.text:00401026 imul    esi
.text:00401028 sar     edx, 3
.text:0040102B mov     ecx, edx
.text:0040102D shr     ecx, 1Fh
.text:00401030 add     edx, ecx
.text:00401032 push    edx

因此有如下结论：

• MagicNumber 为正，imul 和 sar 之间有对乘积的高一半减去乘数的调整，故认定除数为负常量，该 MagicNumber 是求补后的结果，需要对 MagicNumber 再次求补即可得到除数的绝对值。
• MagicNumber 为负，imul 和 sar 之间有对乘积的高一半加上乘数的调整，故认定除数为正常量，只不过大小超过有符号数整数表示范围。
• MagicNumber 为负，imul 和 sar 之间未见调整，故认定除数为负常量。

取模

• 模（除）数为变量时无法优化，根据模（除）数类型选择 div 或 idiv 。
• 模（除）数为常量时可以优化（部分高版本编译器，例如 VS2019）。

被除数无符号，模（除）数为 2 的整数次幂

如果被除数为无符号数，则 $a\mathrm{mod}{2}^n$ 相当于 $a\&(2^n-1)$ 。

被除数有符号，模（除）数为 2 的整数次幂

如果被除数是有符号数，则需要判断被除数小于 0 的情况，因此在取模的同时保留符号位。如果被除数小于 0 则最终结果是负数或 0，如果最后结果是负数需要补上符号位。这里为了避免分支需要将结果减 1 确保最终结果一定为负数再补上符号位，最后再将结果加 1 恢复正确结果。

.text:00401000 mov     eax, [esp+a]
.text:00401004 and     eax, 10000000000000000000000001111111b 	; & 127，并且保留符号位
.text:00401009 jns     short loc_401010                			; 如果 a 是非负数直接跳转到结束
.text:0040100B dec     eax                             			; 减 1 避免结果为 0 的情况计算错误
.text:0040100C or      eax, 11111111111111111111111110000000b 	; 补上符号位
.text:0040100F inc     eax                             			; 恢复前面的减一操作
.text:00401010 loc_401010:                             
.text:00401010 push    eax

对于除数小于 0 的情况，如果是低版本 VC 编译器则采用无分支的取模策略。

.text:00401000 mov     eax, [esp+a]
.text:00401004 cdq
.text:00401005 xor     eax, edx
.text:00401007 sub     eax, edx              ; 如果 a 小于 0 则将 a 取反加 1（a = abs(a)）
.text:00401009 and     eax, 7                ; 模 8
.text:0040100C xor     eax, edx
.text:0040100E sub     eax, edx              ; 如果 a 小于 0 则将取模结果取反加 1
.text:00401010 push    eax

高版本会采用类似除数为正数，被除数为有符号数时的 jns 方法。不过 VS 2022 优化策略和老版本一样。

被除数无符号，模数不为 2 的整数次幂

对于被除数无符号，模数不为 2 的整数次幂的情况，$a\mathrm{mod}b$ 会被编译器优化为 $a-\lfloor \frac{a}{b}\rfloor \times b$，其中 $\lfloor \frac{a}{b}\rfloor$ 会按照被除数无符号，除数为非 2 的整数次幂的除法优化。

以 x % 7 为例，汇编代码如下：

; 无符号除法 ecx = x / 7
.text:004010AF mov     esi, [ebp+x]
.text:004010B2 mov     eax, 24924925h
.text:004010B7 mul     esi
.text:004010B9 mov     ecx, esi
.text:004010BB sub     ecx, edx
.text:004010BD shr     ecx, 1
.text:004010BF add     ecx, edx
.text:004010C1 shr     ecx, 2
; eax = x / 7 * 8 - x / 7 = x / 7 * 7
.text:004010C4 lea     eax, ds:0[ecx*8]
.text:004010CB sub     eax, ecx
; esi = x - x / 7 * 7 = x % 7
.text:004010CD sub     esi, eax
.text:004010CF push    esi

被除数有符号，模数不为 2 的整数次幂

如果模数为正数，则 $a\mathrm{mod}b$ 会同样按照$a-\lfloor \frac{a}{b}\rfloor \times b$ 来进行优化，只不过这里的除法按照被除数有符号，除数为非 2 的整数次幂的情况进行优化。

; 有符号除法 ecx = x / 7
.text:004010AF mov     esi, [ebp+x]
.text:004010B2 mov     eax, 92492493h
.text:004010B7 imul    esi
.text:004010B9 add     edx, esi
.text:004010BB sar     edx, 2
.text:004010BE mov     ecx, edx
.text:004010C0 shr     ecx, 1Fh
.text:004010C3 add     ecx, edx
; eax = x / 7 * 8 - x / 7 = x / 7 * 7
.text:004010C5 lea     eax, ds:0[ecx*8]
.text:004010CC sub     eax, ecx
; esi = x - x / 7 * 7 = x % 7
.text:004010CE sub     esi, eax
.text:004010D0 push    esi

如果模数为负数，结果与模数为正数相同，即 $a\mathrm{mod}b\equiv a\mathrm{mod}\left|b\right|$ 。

控制流程

三目运算符

在不开优化时三目运算会被编译成 if-else 形式，但是开启优化后编译器针对减少程序分支做一些优化。

等式型

等式型三目运算符的形式为 x == a ? b : c 。实际上所有等式型的三目运算符都可以通过 x == 0 ? 0 : -1 转换过来。

x == 0 ? 0 : -1 对应的汇编指令为：

.text:00401003 mov     eax, [ebp+x]		; eax = x
.text:00401006 neg     eax				; CF = eax == 0 ? 0 : 1; eax = -x; 
.text:00401008 sbb     eax, eax			; eax = eax - eax - CF = -CF = x == 0 ? 0 : -1

如果是 x == a ? b : c 则对应的汇编指令为：

.text:00401000 mov     eax, [esp+x]
.text:00401004 sub     eax, a
.text:00401007 neg     eax
.text:00401009 sbb     eax, eax
.text:0040100B and     eax, c - b		; x == a ? 0 : c - b
.text:0040100E add     eax, b			; x == a ? b : c

对于高版本的编译器，针对三目运算会使用 cmovxx 条件传送指令进行优化：

.text:00401003 cmp     [ebp+x], a
.text:00401007 mov     eax, c
.text:0040100C mov     ecx, b
.text:00401011 cmovz   eax, ecx

不等式型

以 x > a ? b : c 为例对应的汇编指令如下：

.text:00401000 mov     ecx, [esp+x]		; ecx = x
.text:00401004 xor     eax, eax			; eax = 0
.text:00401006 cmp     ecx, a
.text:00401009 setle   al				; al = x <= a ? 1 : 0
.text:0040100C dec     eax				; eax = x <= a ? 0 : -1
.text:0040100D and     al, c - b		; eax = x <= a ? 0 : b - c
.text:0040100F add     eax, b			; eax = x <= a ? c : b

对于高版本的编译器，针对三目运算会使用 cmovxx 条件传送指令进行优化：

.text:00401003 cmp     [ebp+x], a
.text:00401007 mov     eax, c			; eax = c
.text:0040100C mov     ecx, b			; ecx = b
.text:00401011 cmovg   eax, ecx			; eax = x > a ? ecx : eax

表达式型

我们定义形如 条件 ? 表达式1 : 表达式2 的三目运算为表达式型三目运算。

以下面的代码为例。

#include <iostream>int main(int argc, char *argv[]) {return argc < 8 ? argc / 8 : argc / 2;
}

VC6.0 编译器生成的汇编代码如下，该编译器将表达式型三目运算按照 if-else 的形式编译成汇编，没有进行减少分支跳转的优化。

.text:00401000 mov     eax, [esp+x]
.text:00401004 cmp     eax, 8
.text:00401007 cdq							; edx = x < 0 ? -1 : 0
.text:00401008 jge     short loc_401013
.text:0040100A and     edx, 7				; edx = x < 0 ? 7 : 0
.text:0040100D add     eax, edx				; eax = x < 0 ? eax + 7 : eax
.text:0040100F sar     eax, 3				; eax >>= 3
.text:00401012 retn
.text:00401013 loc_401013: 
.text:00401013 sub     eax, edx				; eax = x < 0 ? eax + 1 : eax
.text:00401015 sar     eax, 1				; eax >>= 1
.text:00401017 retn

高版本编译器仍会使用 cmovxx 条件传送指令进行优化：

.text:00401003 push    esi					; 保存 esi
.text:00401004 mov     esi, [ebp+x]			; esi = x
.text:00401007 mov     eax, esi
.text:00401009 cdq							; edx = x < 0 ? -1 : 0
.text:0040100A sub     eax, edx				; eax = x < 0 ? x + 1 : x
.text:0040100C mov     ecx, eax				; ecx = x < 0 ? x + 1 : x
.text:0040100E mov     eax, esi
.text:00401010 cdq							; edx = x < 0 ? -1 : 0
.text:00401011 and     edx, 7				; edx = x < 0 ? 7 : 0
.text:00401014 sar     ecx, 1				; ecx = (x < 0 ? x + 1 : x) >> 1
.text:00401016 add     eax, edx				; eax = x < 0 ? x + 7 : x
.text:00401018 sar     eax, 3				; eax =  (x < 0 ? x + 7 : x) >> 3
.text:0040101B cmp     esi, 8
.text:0040101E pop     esi					; 恢复 esi
.text:0040101F cmovge  eax, ecx				; eax = x >= 8 ? (x < 0 ? x + 1 : x) >> 1 : (x < 0 ? x + 7 : x) >> 3

绝对值型

对于 x >= 0 ? x : -x 类型的三目运算符，高版本的 VC 会将其优化为 abs(x) 函数（abs 函数在高版本和低版本实现相同且会内联）。abs(x) 对应的汇编代码如下：

.text:00401000 mov     eax, [esp+x]
.text:00401004 cdq							; edx = x < 0 ? -1 : 0
.text:00401005 xor     eax, edx				; eax = x < 0 ? ~x : x
.text:00401007 sub     eax, edx				; eax = x < 0 ? (~x) + 1 : x

VC6.0 则会直接编译为 if 语句。

.text:00401000 mov     eax, [esp+x]
.text:00401004 test    eax, eax
.text:00401006 jge     short locret_40100A
.text:00401008 neg     eax
.text:0040100A locret_40100A:
... 

if 语句

if 型

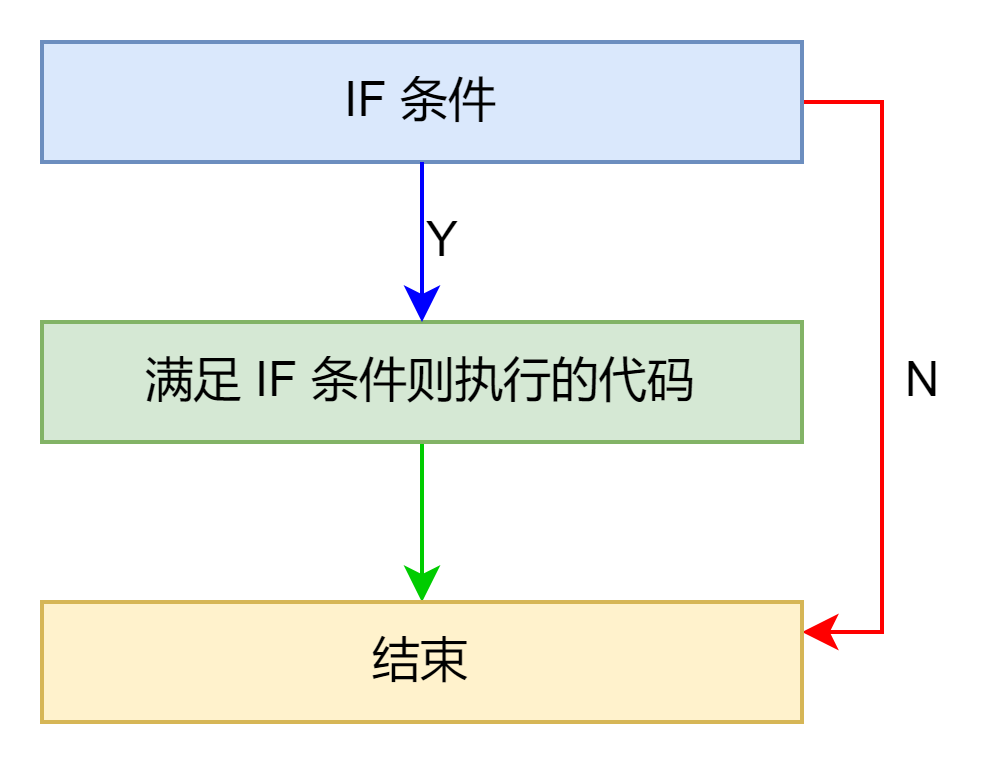
汇编示例如下：

.text:00401003 cmp     [ebp+x], 0
.text:00401007 jle     short loc_401016.text:00401009 push    offset string				; "x > 0"
.text:0040100E call    _puts
.text:00401013 add     esp, 4.text:00401016 loc_401016: 

if-else 型

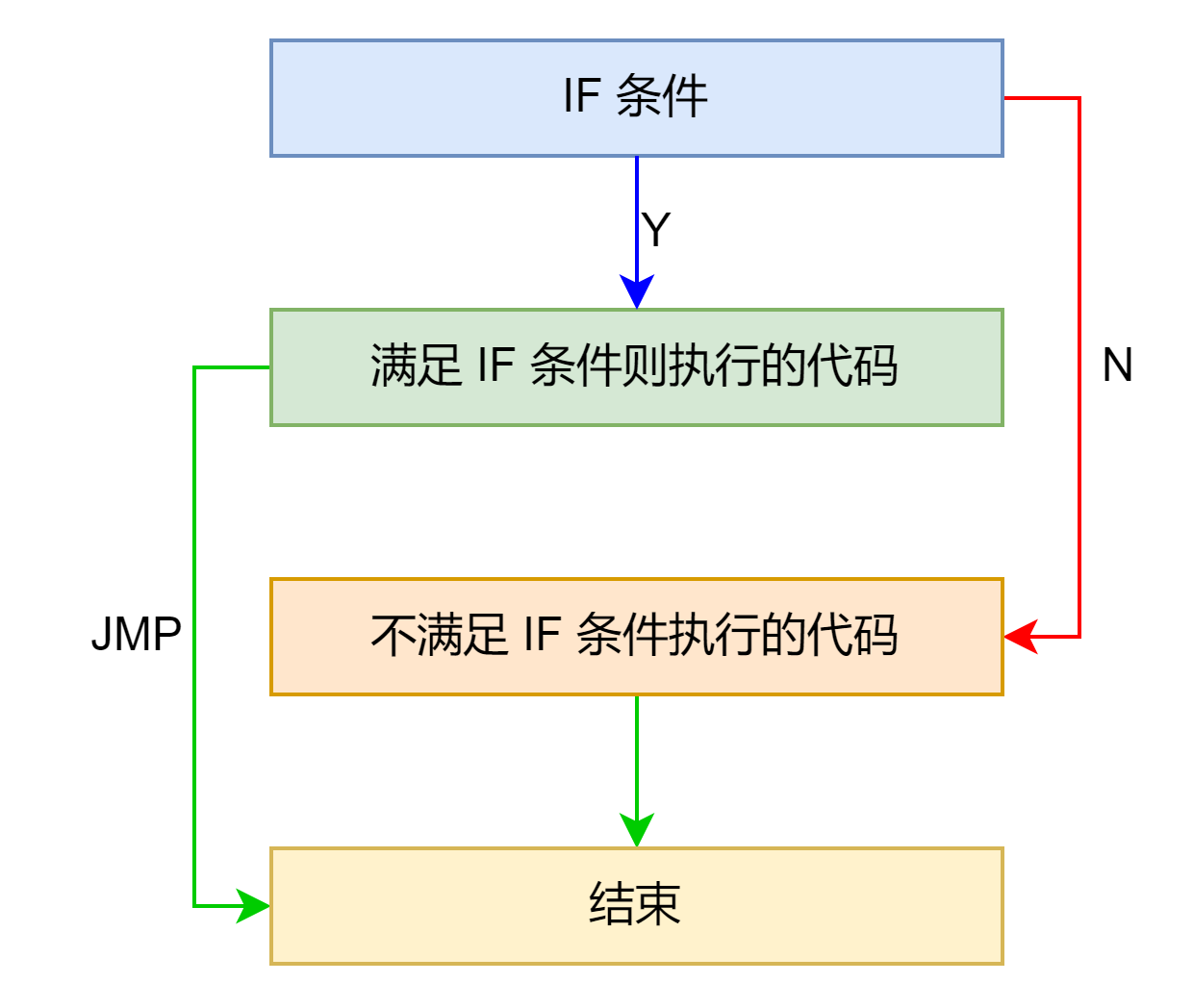
汇编示例如下：

.text:00401003 cmp     [ebp+x], 0
.text:00401007 jle     short loc_401018.text:00401009 push    offset string1                  ; "x > 0"
.text:0040100E call    _puts
.text:00401013 add     esp, 4
.text:00401016 jmp     short loc_401025.text:00401018 loc_401018:
.text:00401018 push    offset string2                  ; "x <= 0"
.text:0040101D call    _puts
.text:00401022 add     esp, 4.text:00401025 loc_401025:      

if-else if-else 型

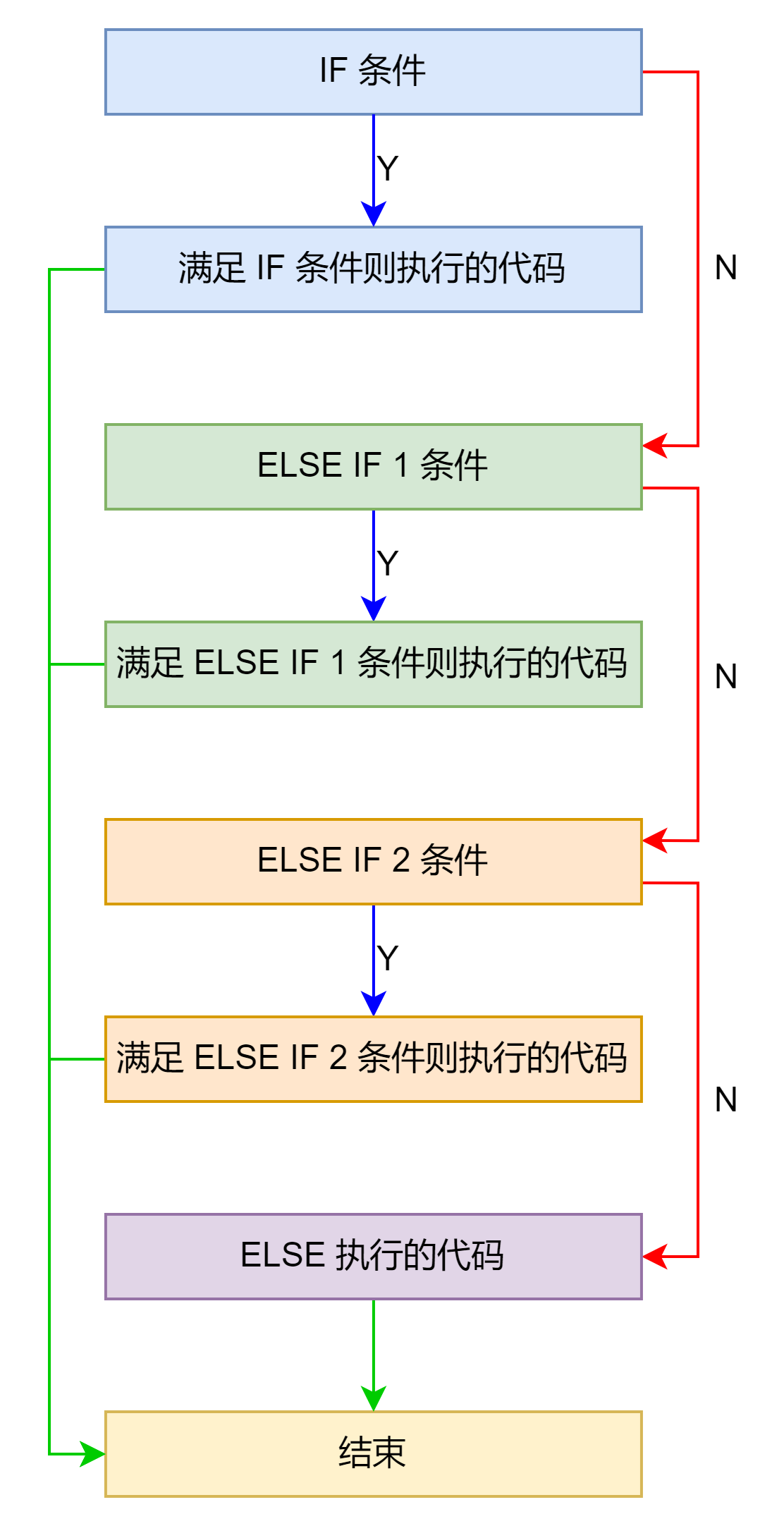
汇编示例如下：

.text:00401003 cmp     [ebp+x], 0
.text:00401007 jle     short loc_401018.text:00401009 push    offset string1                  ; "x > 0"
.text:0040100E call    _puts
.text:00401013 add     esp, 4
.text:00401016 jmp     short loc_40103A.text:00401018 loc_401018:
.text:00401018 cmp     [ebp+x], 0
.text:0040101C jnz     short loc_40102D.text:0040101E push    offset string2                  ; "x == 0"
.text:00401023 call    _puts
.text:00401028 add     esp, 4
.text:0040102B jmp     short loc_40103A.text:0040102D loc_40102D:
.text:0040102D push    offset string3                  ; "x <= 0"
.text:00401032 call    _puts
.text:00401037 add     esp, 4.text:0040103A loc_40103A:    

switch 语句

分支较少

与前面 if 语句不同，switch 语句将满足条件执行的代码放在一起，这样做是为了满足 switch 中不加 break 会继续执行的特性。

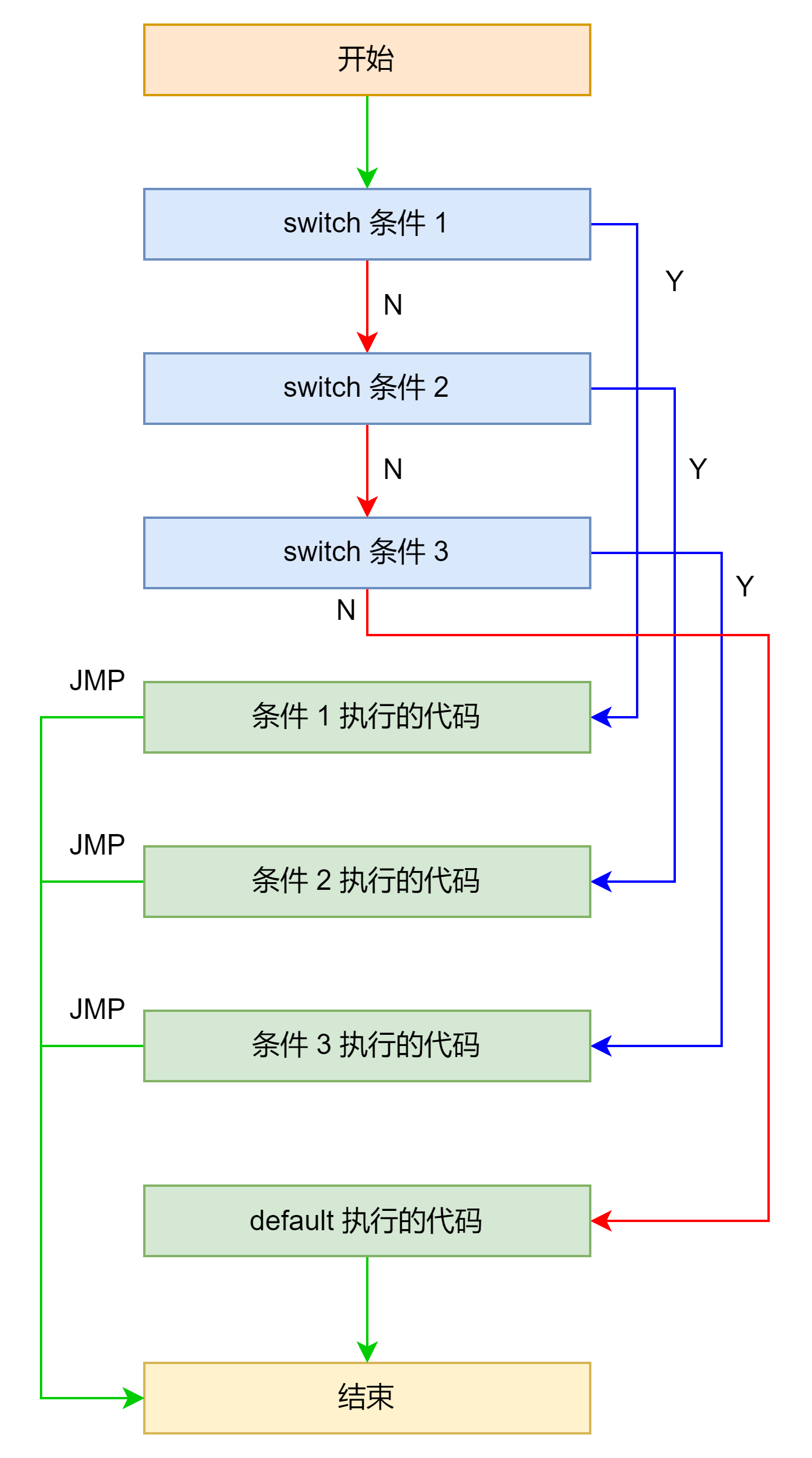
汇编示例如下：

.text:00401004 mov     eax, [ebp+x]
.text:00401007 mov     [ebp+val], eax.text:0040100A cmp     [ebp+val], 0
.text:0040100E jz      short loc_40101E.text:00401010 cmp     [ebp+val], 1
.text:00401014 jz      short loc_40102D.text:00401016 cmp     [ebp+val], 2
.text:0040101A jz      short loc_40103C.text:0040101C jmp     short loc_40104B.text:0040101E loc_40101E:
.text:0040101E push    offset string1                  ; "x == 0"
.text:00401023 call    _puts
.text:00401028 add     esp, 4
.text:0040102B jmp     short loc_401058.text:0040102D loc_40102D:
.text:0040102D push    offset string2                  ; "x == 1"
.text:00401032 call    _puts
.text:00401037 add     esp, 4
.text:0040103A jmp     short loc_401058.text:0040103C loc_40103C:
.text:0040103C push    offset string3                  ; "x == 2"
.text:00401041 call    _puts
.text:00401046 add     esp, 4
.text:00401049 jmp     short loc_401058.text:0040104B loc_40104B:
.text:0040104B push    offset string4                  ; "default"
.text:00401050 call    _puts
.text:00401055 add     esp, 4.text:00401058 loc_401058:

分支较多但比较连续

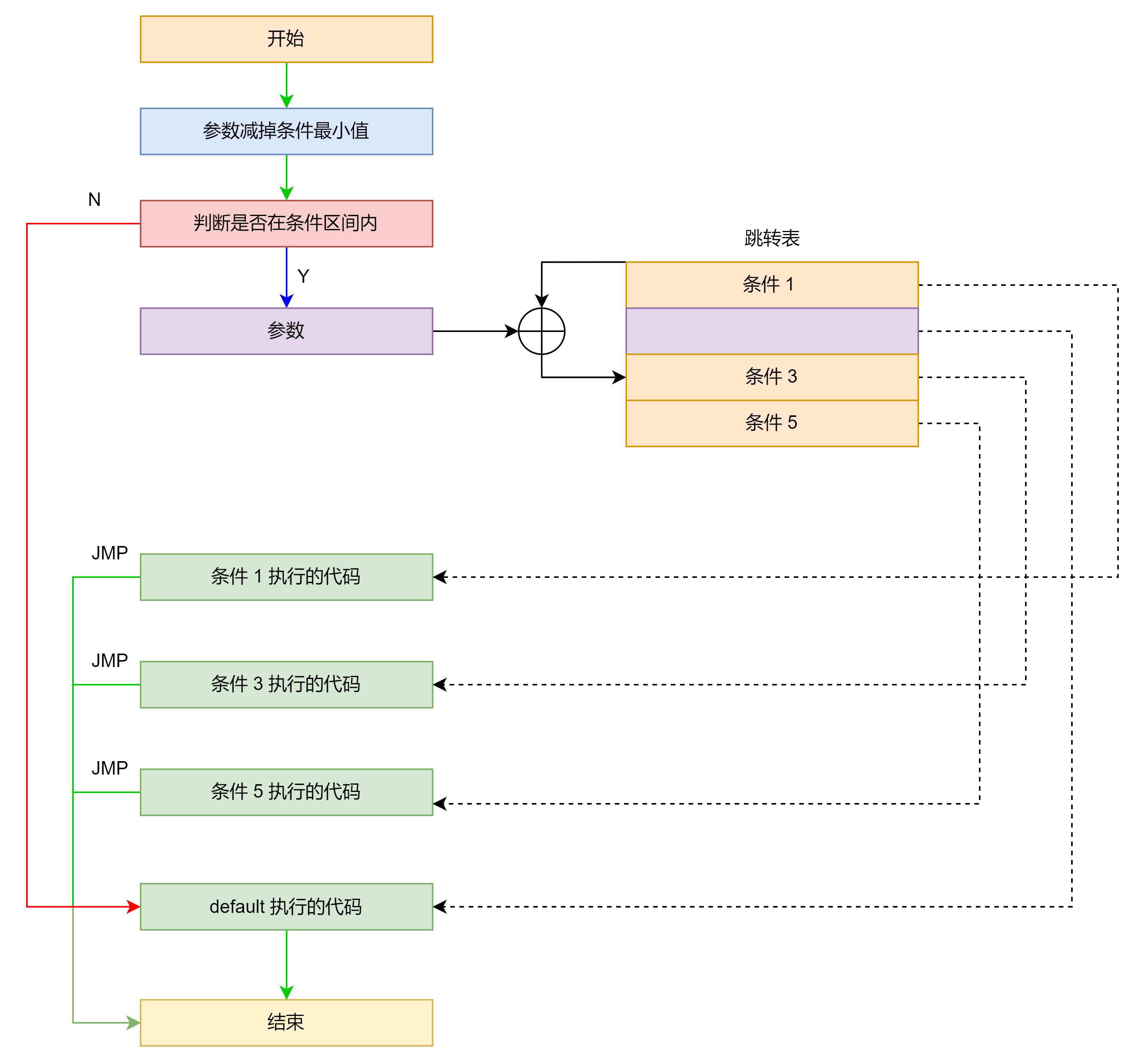
汇编示例如下：

.text:00401074 jpt_40101C dd offset $LN4               ; jump table for switch statement
.text:00401074 dd offset $LN5
.text:00401074 dd offset def_40101C
.text:00401074 dd offset $LN6
.text:00401074 dd offset $LN7.text:00401004 mov     eax, [ebp+x]
.text:00401007 mov     [ebp+val], eax.text:0040100A mov     ecx, [ebp+val]
.text:0040100D sub     ecx, 3                          ; switch 5 cases
.text:00401010 mov     [ebp+val], ecx.text:00401013 cmp     [ebp+val], 4
.text:00401017 ja      short def_40101C                ; jumptable 0040101C default case, case 5.text:00401019 mov     edx, [ebp+val]
.text:0040101C jmp     ds:jpt_40101C[edx*4]            ; switch jump.text:00401023 $LN4:
.text:00401023 push    offset string1                  ; jumptable 0040101C case 3
.text:00401028 call    _puts
.text:0040102D add     esp, 4
.text:00401030 jmp     short loc_40106C.text:00401032 $LN5:
.text:00401032 push    offset string2                  ; jumptable 0040101C case 4
.text:00401037 call    _puts
.text:0040103C add     esp, 4
.text:0040103F jmp     short loc_40106C.text:00401041 $LN6:
.text:00401041 push    offset string3                  ; jumptable 0040101C case 6
.text:00401046 call    _puts
.text:0040104B add     esp, 4
.text:0040104E jmp     short loc_40106C.text:00401050 $LN7:
.text:00401050 push    offset string4                  ; jumptable 0040101C case 7
.text:00401055 call    _puts
.text:0040105A add     esp, 4
.text:0040105D jmp     short loc_40106C.text:0040105F def_40101C:
.text:0040105F push    offset string5                  ; jumptable 0040101C default case, case 5
.text:00401064 call    _puts
.text:00401069 add     esp, 4.text:0040106C loc_40106C:

分支较多且比较不连续

分支较多且比较不连续且 case 最大值和最小值之差在 256 以内，会将跳转表去重然后额外使用一个 byte 数组保存跳转表下标。

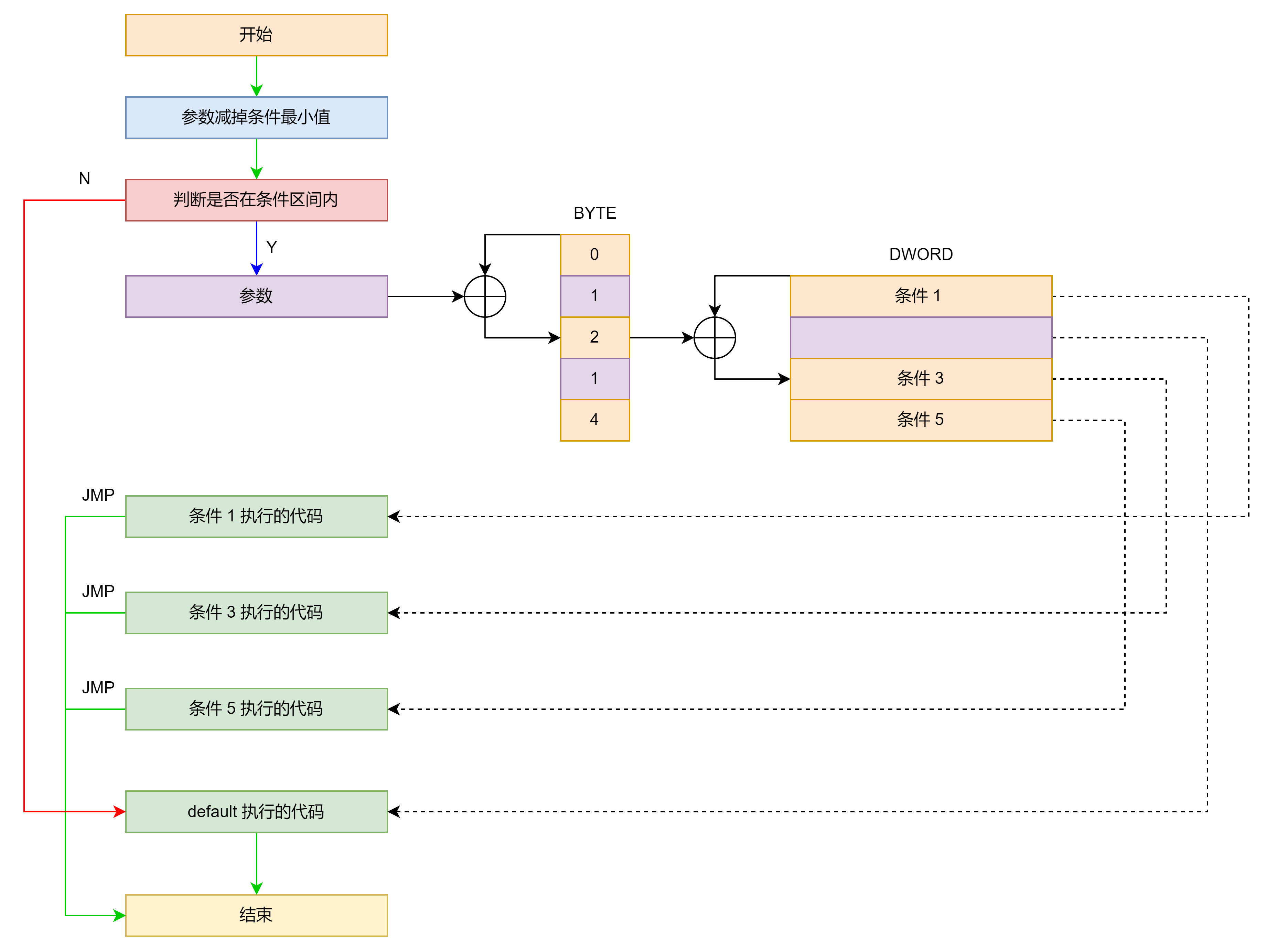
汇编示例如下：

.text:0040107C jpt_401026 dd offset $LN4
.text:0040107C dd offset $LN6                          ; jump table for switch statement
.text:0040107C dd offset $LN7
.text:0040107C dd offset $LN5
.text:0040107C dd offset $LN8.text:00401090 byte_401090 db 0, 4, 4, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4
.text:00401090 db 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 ; indirect table for switch statement
.text:00401090 db 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 2, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4
.text:00401090 db 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4
.text:00401090 db 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4
.text:00401090 db 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4
.text:00401090 db 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4
.text:00401090 db 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3.text:00401004 mov     eax, [ebp+x]
.text:00401007 mov     [ebp+val], eax.text:0040100A mov     ecx, [ebp+val]
.text:0040100D sub     ecx, 3                          ; switch 254 cases
.text:00401010 mov     [ebp+val], ecx.text:00401013 cmp     [ebp+val], 253
.text:0040101A ja      short $LN8                      ; jumptable 00401026 default case, cases 4,5,7-79,81-255.text:0040101C mov     edx, [ebp+val]
.text:0040101F movzx   eax, ds:byte_401090[edx]
.text:00401026 jmp     ds:jpt_401026[eax*4]            ; switch jump.text:0040102D $LN4:
.text:0040102D push    offset string1                  ; jumptable 00401026 case 3
.text:00401032 call    _puts
.text:00401037 add     esp, 4
.text:0040103A jmp     short loc_401076.text:0040103C $LN5:
.text:0040103C push    offset string2                  ; jumptable 00401026 case 256
.text:00401041 call    _puts
.text:00401046 add     esp, 4
.text:00401049 jmp     short loc_401076.text:0040104B $LN6:
.text:0040104B push    offset string3                  ; jumptable 00401026 case 6
.text:00401050 call    _puts
.text:00401055 add     esp, 4
.text:00401058 jmp     short loc_401076.text:0040105A $LN7:
.text:0040105A push    offset string4                  ; jumptable 00401026 case 80
.text:0040105F call    _puts
.text:00401064 add     esp, 4
.text:00401067 jmp     short loc_401076.text:00401069 $LN8:
.text:00401069 push    offset string5                  ; jumptable 00401026 default case, cases 4,5,7-79,81-255
.text:0040106E call    _puts
.text:00401073 add     esp, 4.text:00401076 loc_401076:

分支较多且特别不连续

此时会形成类似二叉树的 if-else 分支嵌套，还会在其中嵌套查表的方法，较为复杂。

循环语句

do-while

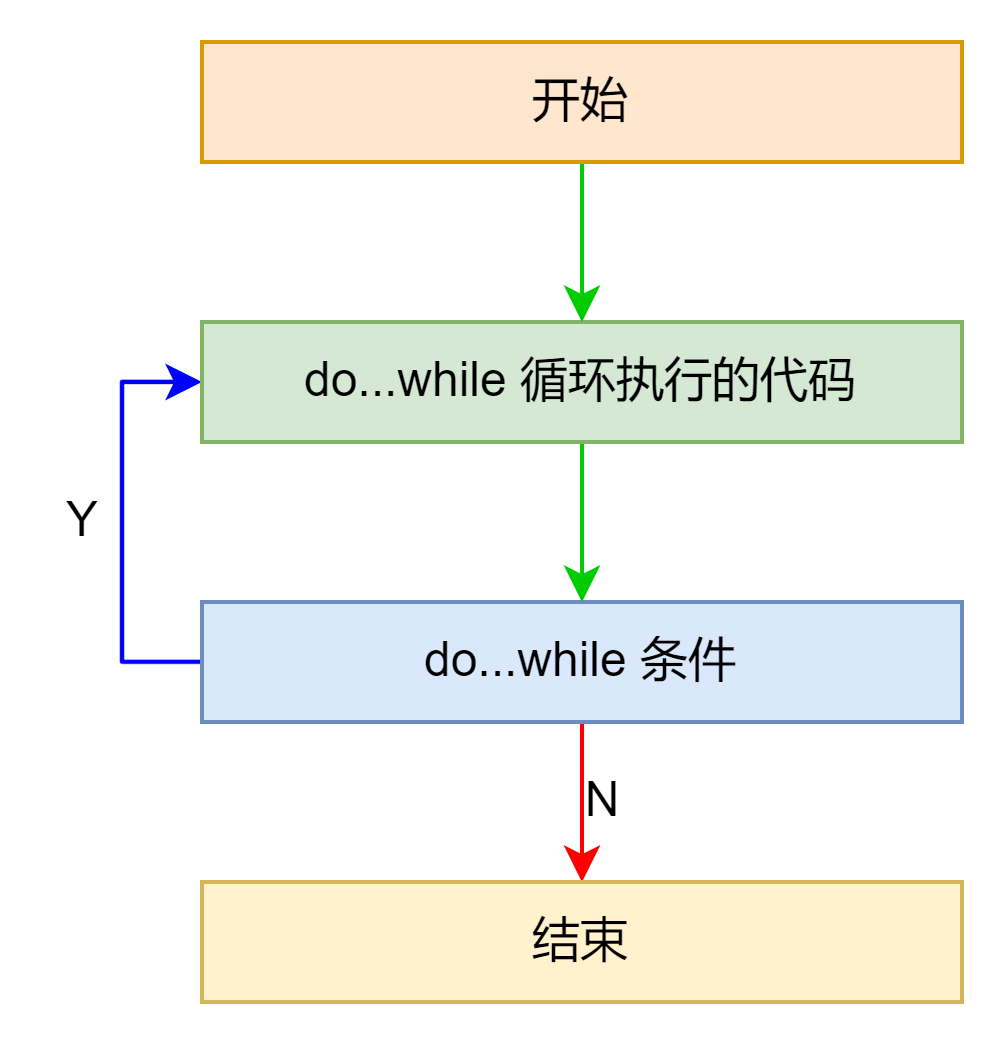
汇编示例如下：

.text:00401003 loc_401003:
.text:00401003 mov     eax, [ebp+x]
.text:00401006 add     eax, 1
.text:00401009 mov     [ebp+x], eax.text:0040100C mov     ecx, [ebp+x]
.text:0040100F cmp     ecx, [ebp+y]
.text:00401012 jl      short loc_401003

while

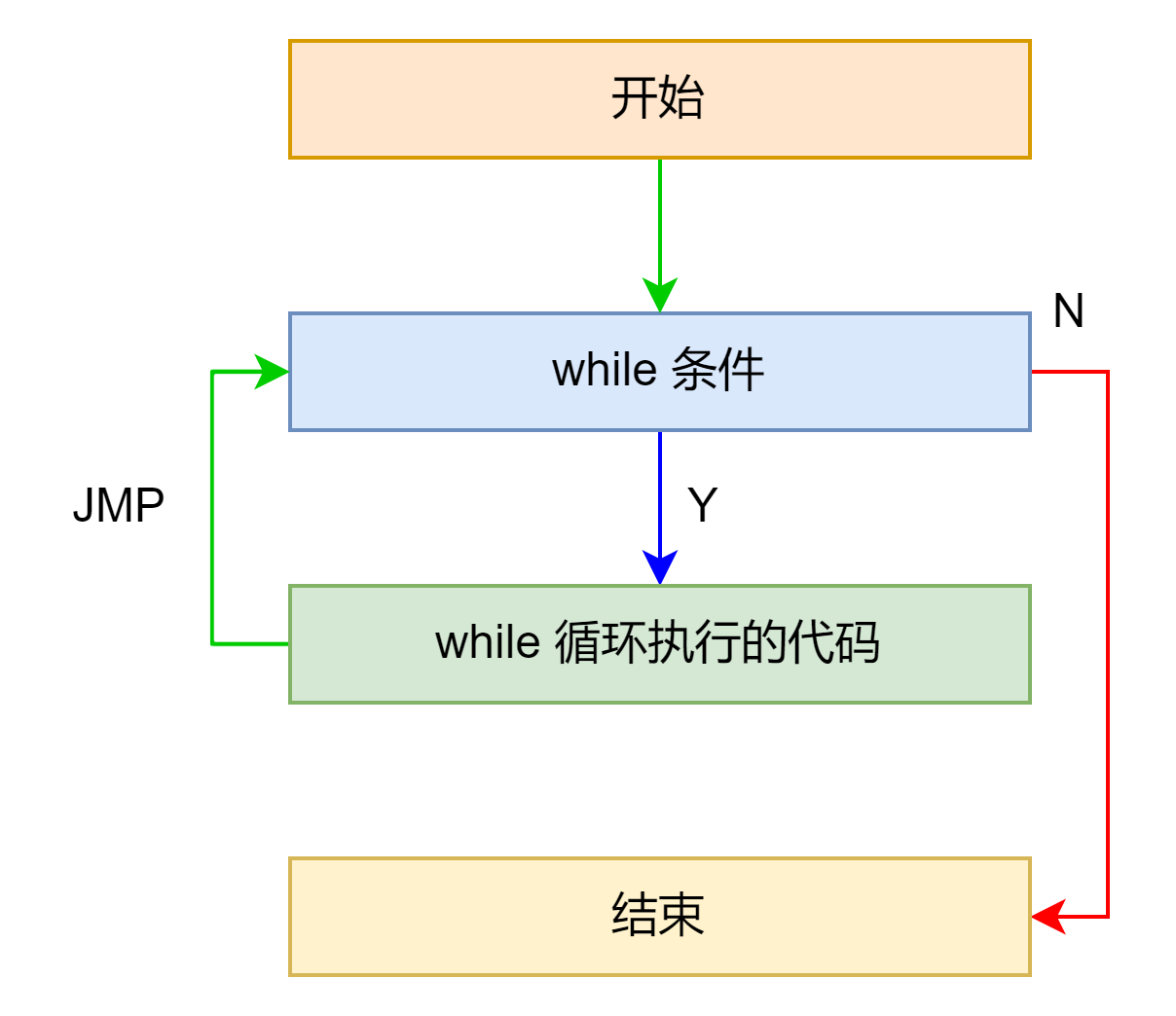
.text:00401003 loc_401003:
.text:00401003 mov     eax, [ebp+x]
.text:00401006 cmp     eax, [ebp+y]
.text:00401009 jge     short loc_401016.text:0040100B mov     ecx, [ebp+x]
.text:0040100E add     ecx, 1
.text:00401011 mov     [ebp+x], ecx
.text:00401014 jmp     short loc_401003.text:00401016 loc_401016:  

for

函数

这篇关于kr 第三阶段（五）32 位逆向的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---