《推荐系统开发实战》之基于点击率预估的推荐算法介绍和案例开发实战

本文主要是介绍《推荐系统开发实战》之基于点击率预估的推荐算法介绍和案例开发实战，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

转载请注明出处：http://blog.csdn.net/gamer_gyt
博主微博：http://weibo.com/234654758
Github：https://github.com/thinkgamer
公众号：搜索与推荐Wiki
个人网站：http://thinkgamer.github.io

本系列之前介绍的都是一些基本的推荐算法，将这些算法真正应用到工业界（即应用推荐系统的地方，如电商网站、广告推广等）其实是很难的。并不是说这些算法没有用武之地，而是要根据具体的场景来判断是否能使用推荐系统。本篇会先对传统的推荐算法进行总结和说明，然后对目前业界用得最广的GBDT算法和LR算法进行介绍。

传统推荐算法的局限和应用

1. 海量数据

例如，协同过滤算法能够容易地为“千万”级的用户提供推荐，但是对于电子商务网站（其用户数和物品数往往以“亿”来计量），协同过滤算法就很难提供服务了。
在协同过滤算法中，能利用最新的信息及时为用户产生相对准确的用户兴趣度预测，或者进行推荐。但是面对日益增多的用户，数据量急剧增加，算法的扩展性问题（即适应系统规模不断扩大的问题）成为制约推荐系统实施的重要因素。
与基于模型的算法相比，全局数值算法虽然节约了为建立模型而花费的训练时间，但是其用于识别“最近邻居”算法的计算量会随着用户和物品的增加而急剧增大。
对于以“亿”来计量的用户和物品，通常的算法会遇到严重的扩展性瓶颈问题。对于采用了协同过滤技术的推荐系统，该问题解决不好，直接会影响其实时性。推荐系统的实时性越好、精确度越高，该系统才越会被用户所接受。

2. 稀疏性

伴随着海量数据的一个问题便是数据的稀疏性。
在电子商务网站中，活跃用户所占的比例很小，大部分用户都是非活跃用户，非活跃用户购买或点击的商品数目也很少。因此，在使用协同过滤算法构建矩阵时，矩阵会非常稀疏；使用基于内容的推荐算法为用户构建的偏好矩阵也是非常稀疏的。这样，一方面难以找到最近邻的用户集，或者难以准确地得到用户行为偏好；另一方面，在计算的过程中会消耗大量的资源。

3. 实时性

实时性是评判一个推荐系统能否及时捕捉用户兴趣变化的重要指标。推荐系统的实时性主要包括两方面：

推荐系统能实时地更新推荐列表来满足用户新的行为变化；
推荐系统能把新加入系统的物品推荐给用户。
而传统的协同过滤算法每次都需要计算所有用户和物品的数据，难以在“秒”级内捕捉到用户的实时兴趣变化。

点击率预估在推荐系统中的应用

点击率预估（CTR）最早应用于搜索广告中。时至今日，点击率预估的应用场景不仅从最开始的搜索广告扩展到展示广告、信息流广告等各种各样的广告，而且在推荐系统的场景中也得到了广泛应用。

从用户的点击行为来分析，“点击率预估”在广告或推荐场景中的应用是一致的。广告的“点击率预估”计算的是用户点击广告的可能性；而在推荐系统中，推荐商品也被预测用户的兴趣，如果用户对一个商品感兴趣便会去点击。这也是近些年CTR在推荐系统中被广泛应用的原因。
目前在CTR领域应用较多的算法包含LR、GBDT、XGBoost、FM、FFM、神经网络算法等，这些算法也被应用到推荐系统中。其中，GBDT是一种非线性算法，基于集成学习中的Boosting（提升方法）思想，每次迭代都在减少残差的梯度方向新建立一棵决策树，迭代多少次就会生成多少棵决策树。

GBDT算法的思想使其具有天然优势：可以发现多种有区分性的特征和特征组合；决策树的路径可以直接作为LR输入特征使用；省去了人工寻找特征、特征组合的步骤。

点击率预估算法的基础

集成学习

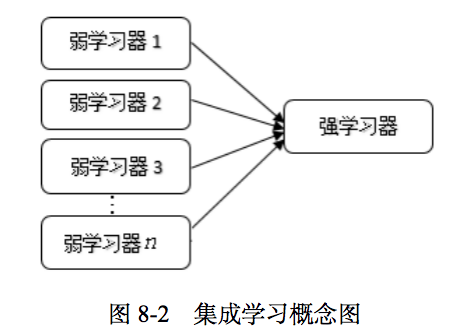
机器学习算法分为有监督学习算法和无监督学习算法。在有监督学习算法中，我们的目标是学习出一个稳定的且在各个方面都表现较好的模型。但实际情况往往不理想，有时只能得到多个在某些方面表现比较好的“弱监督模型”。集成学习就是组合多个“弱监督模型”以得到一个更好、更全面的“强监督模型”。
集成学习本身不是一个单独的机器学习算法，而是通过构建并组合多个弱学习器来完成学习任务，如图所示

集成学习包括Boosting算法（提升法）、Bagging算法（自助法）和Stacking算法（融合法）三种算法。 > 那么三种集成学习方法的具体含义是什么呢？

导数、偏导数、方向导数、梯度

了解这些概念是学习点击率预估算法的基础，很多算法都是基于梯度下降进行求解的，但要了解梯度下降就必须要明白导数，偏导数，方向导数的概念。

这里不展开介绍，大家可以从《推荐系统开发实战》中获取内容。

GBDT算法

GBDT算法（Gradient Boosting Decision Tree）又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法。

该算法中构建多棵决策树组成，所有决策树的结论累加起来作为最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。

GBDT的算法原理

GBDT算法可以看成是T棵树组成的加法模型，其对应的公式如下：

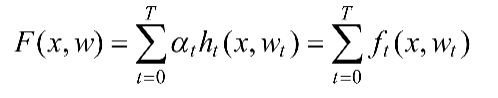
式中：

x：输入样本；
w：模型参数；
h：分类回归树；
α：每棵树的权重。
GBDT算法的实现过程如下。
（1）初始化函数F0常量（其中L为损失函数）：

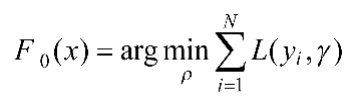
（2）循环执行M次，建立M棵分类回归树。创建第m（m=1,2,…,M）棵树的过程见步骤（3）~步骤（6）。
（3）计算第m棵树对应的响应值（伪残差），计算公式如下：

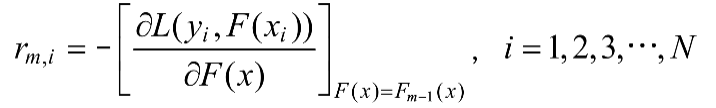
（4）使用CART回归树拟合数据得到第m棵树的叶子节点区域Rj,m，其中j=1,2,… ,Jm。
（5）对于j=1,2, … ,Jm，计算：

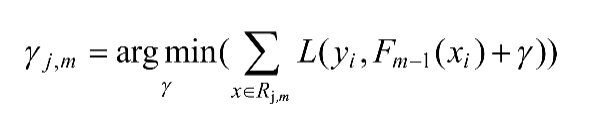
（6）更新Fm为:

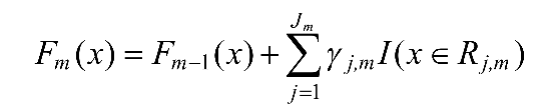
（7）输出Fm(x)

具体的GBDT算法实例，这里不展开介绍。

回归分析

回归分析算法（Regression Analysis Algorithm）是机器学习算法中最常见的一类机器学习算法。就是利用样本（已知数据），产生拟合方程，从而（对未知数据）进行预测。例如有一组随机变量X（x1，x2，x3，…）和另外一组随机变量Y（y1，y2，y3，…），那么研究变量X与Y之间关系的统计学方法就叫作回归分析。因为这里X和Y是单一对应的，所以这里是一元线性回归。

回归分析算法分为线性回归算法和非线性回归算法。

线性回归

线性回归可以分为一元线性回归和多元线性回归。当然线性回归中自变量的指数都是1，这里的线性并非真的是指用一条线将数据连起来，也可以用一个二维平面、三维曲面等。
一元线性回归：只有一个自变量的回归。例如房子面积（Area）和房子总价（Money）的关系，随着面积（Area）的增大，房屋价格也是不断增加。这里的自变量只有面积，所以是一元线性回归。
多元线性回归：自变量大于或等于两个的回归。例如房子面积（Area）、楼层（floor）和房屋价格（Money）的关系，这里自变量有两个，所以是二元线性回归。
典型的线性回归方程如下：

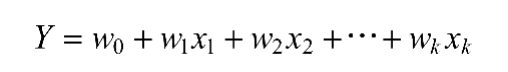
在统计意义上，如果一个回归等式是线性的，那么它相对于参数就必须是线性的。如果相对于参数是线性的，那么即使相对于样本变量的特征是二次方或多次方的，这个回归模型也是线性的。例如下面的式子：

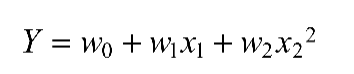
甚至可以使用对数或指数去形式化特征，如下：

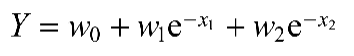
非线形回归

有一类模型，其回归参数不是线性的，也不能通过转换的方法将其变为线性的参数，这类模型称为非线性回归模型。非线性回归可以分为一元回归和多元回归。非线性回归中至少有一个自变量的指数不为1。回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫作一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫作多元回归分析。
例如下面的两个回归方程：

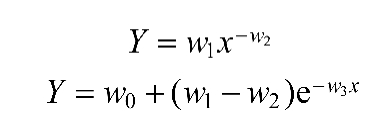
与线性回归模型不一样的是，这些非线性回归模型的特征因子对应的参数不止一个。

广义线性回归

有些非线性回归也可以用线性回归的方法来进行分析，这样的非线性回归叫作广义线性回归。典型的代表是Logistic回归。

LR算法

逻辑回归与线性回归本质上是一样的，都是通过误差函数求解最优系数，在形式上只不过是在线性回归上增加了一个逻辑函数。与线性回归相比，逻辑回归（Logistic Regression，LR）更适用于因变量为二分变量的模型，Logistic 回归系数可用于估计模型中每个自变量的权重比。

我们都知道LR算法使用的是Sigmoid函数作为结果值的区分函数，那么LR为什么要使用Sigmoid呢？

LR的算法原理

机器学习模型实际上把决策函数限定在某一组条件下，这组限定条件就决定了模型的假设空间。当然，还希望这组限定条件简单而合理。
逻辑回归模型所做的假设是：

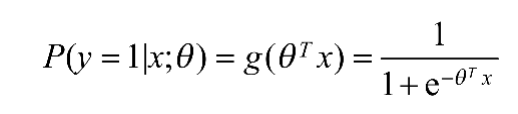
这里的g(h)就是Sigmoid函数，相应的决策函数为：

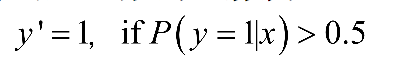
选择0.5作为阈值是一般的做法，实际应用时，特定的情况下可以选择不同的阈值。如果对正例的判别准确性要求高，可以使阈值大一些；如果对正例的召回要求高，则可以使阈值小一些。
在函数的数学形式确定之后，就要求解模型中的参数了。统计学中常用的一种数学方法是最大似然估计，即找到一组参数，使得在这组参数条件下数据的似然度（概率）更大。在逻辑回归算法中，似然函数可以表示为：

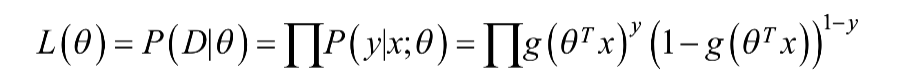
取对数，可以得到对数形式的似然函数：

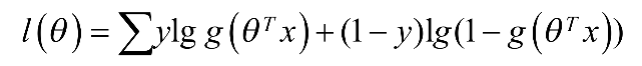
同样这里也使用损失函数来衡量模型预测结果准确的程度，这里采用lg损失函数，其在单条数据上的定义为：

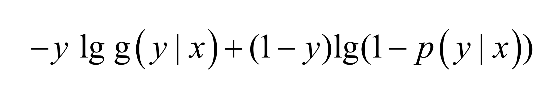
如果取整个数据集上的平均lg损失，可以得到：

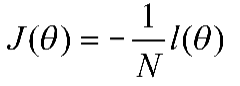
在逻辑回归模型中，最大化似然函数和最小化lg损失函数实际上是等价的。对于该优化问题，存在多种求解方法，这里以梯度下降的情况为例说明。基本步骤如下：

沿梯度负方向选择一个较小的步长可以保证损失函数的值是减小的，另外，逻辑回归模型的损失函数是凸函数（加入正则项后是严格凸函数），可以保证找到的局部最优值是全局最优值。

正则化

当模型中参数过多时，容易产生过拟合，这时就要控制模型的复杂度，其中最常见的做法是在目标中加入正则项，通过惩罚过大的参数来防止过拟合。常见的正则化方法包括L1 正则化和L2 正则化。其分别对应如下两个公式：

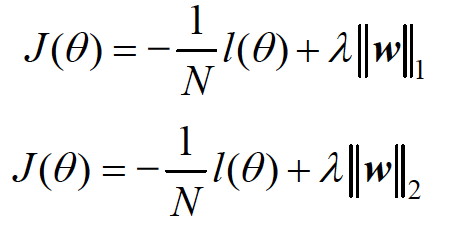
L1 正则化是指权值向量w 中各个元素的绝对值之和，通常表示为||w||1。
L2 正则化是指权值向量w 中各个元素的平方和然后再求平方根（可以看到Ridge 回归
的L2 正则化项有平方符号），通常表示为||w||2。

模型融合

背景介绍

在CTR 预估问题发展初期，使用最多的方法就是逻辑回归（LR），LR 使用了Sigmoid 变换将函数值映射到0~1 区间，映射后的函数值就是CTR 的预估值。LR 属于线性模型，容易并行化，可以轻松处理上亿条数据，但是学习能力十分有限，需要大量的特征工程来增强模型的学习能力。
GBDT 是一种常用的非线性模型，它基于集成学习中的Boosting 思想，每次迭代都在减少残差的梯度方向新建立一棵决策树，迭代多少次就会生成多少棵决策树。GBDT 的思想使其具有天然优势，可以发现多种有区分性的特征及特征组合。决策树的路径可以直接作为LR 输入特征使用，省去了人工寻找特征、特征组合的步骤。这种通过GBDT 生成LR 特征的方式（GBDT+LR），业界已有实践（Facebook、Kaggle 等），且取得了不错的效果。

为什么使用GBDT和LR进行模型融合

在介绍模型融合之前，需要先了解下面两个问题。

为什么使用集成的决策树

一棵树的表达能力很弱，不足以表达多个有区分性的特征组合，多棵树的表达能力更强一些。GBDT 中，每棵树都在学习前面的树存在的不足，迭代多少次就会生成多少棵树。按Facebook的论文及Kaggle 竞赛中的GBDT+LR 融合方式，多棵树正好满足LR 每条训练样本可以通过GBDT 映射成多个特征的需求。

为什么使用GBDT 构建决策树而不是RandomForest（RF）

RF（随机森林）也是多棵树组成的，但从效果上有实践证明不如GBDT。对于GBDT 前面的树，特征分裂主要体现对多数样本有区分度的特征；对于后面的树，主要体现的是经过前N棵树，残差仍然较大的少数样本。优先选用在整体上有区分度的特征，再选用针对少数样本有区分度的特征，这样的思路更加合理，这也是用GBDT 的原因。

GBDT+LR 模型融合的原理

GBDT+LR 模型融合思想来源于Facebook 公开的论文Practical Lessons from Predicting
Clicks on Ads at Facebook。其主要思想是：GBDT 每棵树的路径直接作为LR 的输入特征使用。
即用已有特征训练GBDT 模型，然后利用GBDT 模型学习到的树来构造新特征，最后把这些新特征加入原有特征一起训练模型。构造的新特征向量是取值0/1 的，向量的每个元素对应于GBDT 模型中树的叶子节点。若一个样本点通过某棵树最终落在这棵树的一个叶子节点上，那么在新特征向量中这个叶子节点对应的元素值为1，而这棵树的其他叶子节点对应的元素值为0。新特征向量的长度等于GBDT 模型里所有树包含的叶子节点数之和。在Facebook 的公开论文中，有一个例子，如图8-10 所示。

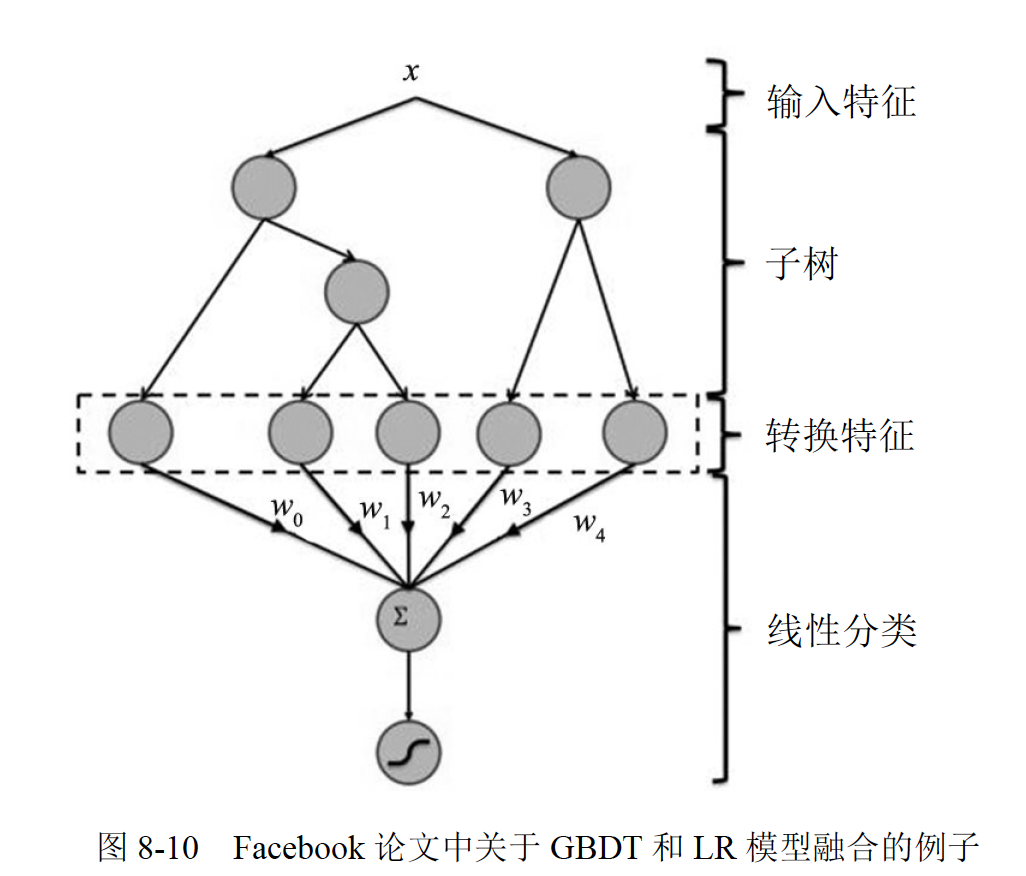
图8-10 中共有两棵树，x 为一条输入样本，遍历两棵树后，x 样本分别落到两棵树的叶子节点上，每个叶子节点对应LR一维特征，那么通过遍历树就得到了该样本对应的所有LR特征。构造的新特征向量是取值0/1 的。举例来说：图8-10 中有两棵子树，左子树有三个叶子节点，右子树有两个叶子节点，最终的特征即为五维的向量。对于输入x，假设x 落在左子树第一个节点时，编码[1,0,0]，落在右子树第二个节点时编码[0,1]，则整体的编码为[1,0,0,0,1]，这类编码作为特征，输入到LR 中进行分类。