基于Or-Tools的指派问题建模求解（PythonAPI）

本文主要是介绍基于Or-Tools的指派问题建模求解（PythonAPI），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

指派问题（又称为分配问题，assignment problem）

指派问题（又称为分配问题，assignment problem）可以抽象概括为：将n个任务（或物品）分配给m个员工（或背包）的问题。其中，最简单的平衡指派模型是指任务数量和员工数量相等的情形。然而，现实生活中的问题大多是任务数量大于员工数量且员工能力有限的广义指派问题（generalized assignment problem，GAP）。GAP是经典的组合优化问题，许多领域的容量约束问题都可以被抽象为GAP进行求解，如机器调度问题、有容量约束的设施选址问题、供应链问题及车辆路径问题等。

广义指派模型
GAP问题可以描述为：将n个相互独立的任务分配给m个员工，一个任务智能由一个员工来完成，一个员工可以完成多项任务，但员工完成任务的总时间不得超过给定限制。

对于$i=1,...,m$；$j=1,...,n$，定义0-1决策变量x_ij=1，表示任务j分配给员工i。令 I = { i ∣ i = 1 , ⋯ , m } I=\{i | i=1,\cdots,m\} I={i∣i=1,⋯,m}为员工集合， J = { j ∣ j = 1 , ⋯ , n } J=\{j | j=1, \cdots, n\} J={j∣j=1,⋯,n}为任务集合，$b_i$表示员工自身的工作时长限制，$r_{ij}$表示员工$i$完成任务$j$需要的时长，$c_{ij}$表示员工$i$完成任务$j$所消耗的资源或产生的收益。最终目标函数为成本最小或收益最大，则GAP可表述为
$$\begin{array}{r}\max 或\min \sum _{i\in I}\sum _{j\in J}{c}_{ij}{x}_{ij}\end{array}$$$s.t.$
∑ j ∈ J r i j x i j ≤ b i , ∀ i ∈ I ∑ i ∈ I x i j = 1 , ∀ j ∈ J x i j ∈ { 0 , 1 } , ∀ j ∈ J \begin{align} \sum_{j \in J} r_{ij}x_{ij} \leq b_i, \quad \forall i \in I \\ \sum_{i \in I}x_{ij}=1, \quad \forall j \in J \\ x_{ij} \in \{0,1\}, \quad \forall j \in J \end{align} j∈J∑​rij​xij​≤bi​,∀i∈Ii∈I∑​xij​=1,∀j∈Jxij​∈{0,1},∀j∈J​​
具有上述形式的整数规划模型被称为广义指派模型。

基于Or-Tools的指派问题建模求解（PythonAPI）

在这个例子中，有5个工人(编号0-4)和4个任务(编号0-3)，将工人分配给任务的成本如下表所示：

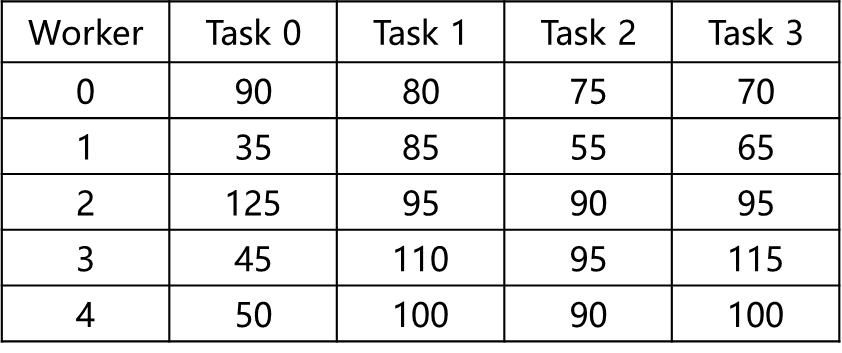
目标为最小化总成本，约束为每个工人最多完成一个任务，每个任务只能由一个工人完成。这个问题中由于工人数多于任务数，因此有一个工人分不到任务。

导入pywraplp库

from ortools.linear_solver import pywraplp

数据准备

costs = [[90, 80, 75, 70],[35, 85, 55, 65],[125, 95, 90, 95],[45, 110, 95, 115],[50, 100, 90, 100],
]
num_workers = len(costs)  # 工人数量
num_tasks = len(costs[0])  # 任务数量

声明MIP求解器

solver = pywraplp.Solver.CreateSolver("SCIP")

初始化决策变量

x = {}
for i in range(num_workers):for j in range(num_tasks):x[i, j] = solver.IntVar(0, 1, "")

初始化约束条件

# 每个员工至多完成一项任务
for i in range(num_workers):solver.Add(solver.Sum([x[i, j] for j in range(num_tasks)]) <= 1)# 每项任务只能由一个员工完成
for j in range(num_tasks):solver.Add(solver.Sum([x[i, j] for i in range(num_workers)]) == 1)

目标函数

objective_terms = []
for i in range(num_workers):for j in range(num_tasks):objective_terms.append(costs[i][j] * x[i, j])
solver.Minimize(solver.Sum(objective_terms))

调用求解器

status = solver.Solve()

打印结果

if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:print(f"Total cost = {solver.Objective().Value()}\n")for i in range(num_workers):for j in range(num_tasks):# Test if x[i,j] is 1 (with tolerance for floating point arithmetic).if x[i, j].solution_value() > 0.5:print(f"Worker {i} assigned to task {j}." + f" Cost: {costs[i][j]}")
else:print("No solution found.")

求解结果

Total cost = 265.0
Worker 0 assigned to task 3. Cost = 70
Worker 1 assigned to task 2. Cost = 55
Worker 2 assigned to task 1. Cost = 95
Worker 3 assigned to task 0. Cost = 45

完整代码

from ortools.linear_solver import pywraplpdef main():# Datacosts = [[90, 80, 75, 70],[35, 85, 55, 65],[125, 95, 90, 95],[45, 110, 95, 115],[50, 100, 90, 100],]num_workers = len(costs)num_tasks = len(costs[0])# Solver# Create the mip solver with the SCIP backend.solver = pywraplp.Solver.CreateSolver("SCIP")if not solver:return# Variables# x[i, j] is an array of 0-1 variables, which will be 1# if worker i is assigned to task j.x = {}for i in range(num_workers):for j in range(num_tasks):x[i, j] = solver.IntVar(0, 1, "")# Constraints# Each worker is assigned to at most 1 task.for i in range(num_workers):solver.Add(solver.Sum([x[i, j] for j in range(num_tasks)]) <= 1)# Each task is assigned to exactly one worker.for j in range(num_tasks):solver.Add(solver.Sum([x[i, j] for i in range(num_workers)]) == 1)# Objectiveobjective_terms = []for i in range(num_workers):for j in range(num_tasks):objective_terms.append(costs[i][j] * x[i, j])solver.Minimize(solver.Sum(objective_terms))# Solvestatus = solver.Solve()# Print solution.if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:print(f"Total cost = {solver.Objective().Value()}\n")for i in range(num_workers):for j in range(num_tasks):# Test if x[i,j] is 1 (with tolerance for floating point arithmetic).if x[i, j].solution_value() > 0.5:print(f"Worker {i} assigned to task {j}." + f" Cost: {costs[i][j]}")else:print("No solution found.")if __name__ == "__main__":main()

这篇关于基于Or-Tools的指派问题建模求解（PythonAPI）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---