本文主要是介绍如何理解傅立叶级数公式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本篇为《信号处理》系列博客的第二篇,该系列博客主要记录信号处理相关知识的学习过程和自己的理解,方便以后查阅。
文章原地址:《如何理解傅立叶级数公式?》
如何理解傅立叶级数公式
- 1 对周期函数进行分解的猜想
- 2 分解的思路
- 2.1 常数项
- 2.2 通过sin(x),cos(x)进行分解
- 2.3 保证组合出来周期为T
- 2.4 调整振幅
- 2.5 小结
- 3 s i n ( x ) sin(x) sin(x)的另外一种表示方法
- 3.1 e i ω t e^{i\omega t} eiωt
- 3.2 通过e^{i\omega t}表示sin(t)
- 4 通过频域来求系数
- 4.1 函数是线性组合
- 4.2 如何求正交基的坐标
- 4.3 如何求sin(nt)基下的坐标
- 4.4 更一般的
本文会对公式进行细节的、代数上的解释。
1 对周期函数进行分解的猜想
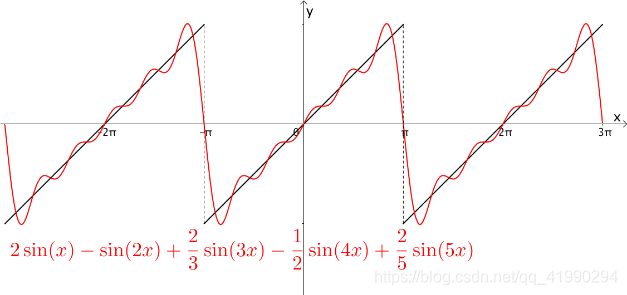
拉格朗日等数学家发现某些周期函数可以由三角函数的和来表示,比如下图中,黑色的斜线就是周期为 2 π 2\pi 2π的函数,而红色的曲线是三角函数之和,可以看出两者确实近似:
而另外一位数学家:

让·巴普蒂斯·约瑟夫·傅里叶男爵(1768 -1830)猜测任意周期函数都可以写成三角函数之和。
2 分解的思路
假设 f ( x ) f(x) f(x)是周期为 T T T的函数,傅里叶男爵会怎么构造三角函数的和,使之等于 f ( x ) f(x) f(x)?
2.1 常数项
对于 y = C , C ∈ R y=C,C\in\mathbb{R} y=C,C∈R这样的常数函数:
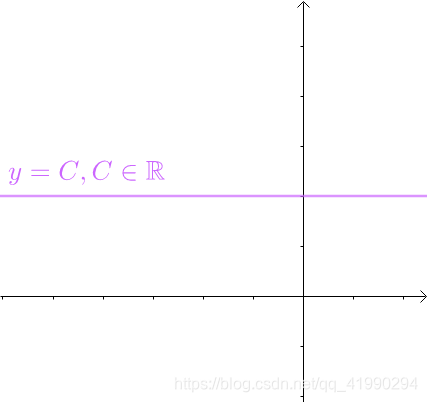
根据周期函数的定义,常数函数是周期函数,周期为任意实数。
所以,分解里面得有一个常数项。
2.2 通过sin(x),cos(x)进行分解
首先, s i n ( x ) , c o s ( x ) sin(x),cos(x) sin(x),cos(x)是周期函数,进行合理的加减组合,结果可以是周期函数。
其次,它们的微分和积分都很简单。
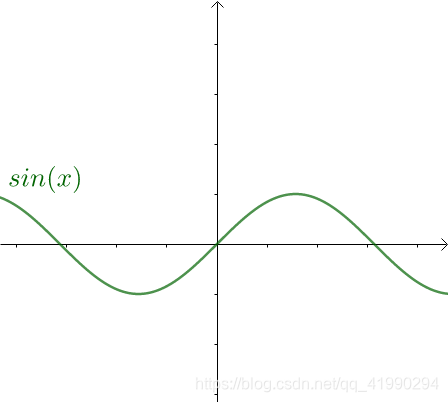
然后, s i n ( x ) sin(x) sin(x)是奇函数,即:

从图像上也可以看出,sin(x)关于原点对称,是奇函数:
而奇函数与奇函数加减只能得到奇函数,即:
f odd ± f odd = f odd f_{\text{odd}}\pm f_{\text{odd}}=f_{\text{odd}} fodd±fodd=fodd
其中, f odd f_{\text{odd}} fodd表示奇函数。
而 c o s ( x ) cos(x) cos(x)是偶函数,即:
c o s ( x ) = c o s ( − x ) cos(x)=cos(-x) cos(x)=cos(−x)
从图像上也可以看出,cos(x)关于Y轴对称,是偶函数:

同样的,偶函数与偶函数加减只能得到偶函数,即:
f even ± f even = f even f_{\text{even}}\pm f_{\text{even}}=f_{\text{even}} feven±feven=feven
其中, f even f_{\text{even}} feven表示偶函数。
但是任意函数可以分解和奇偶函数之和:
f ( x ) = f ( x ) + f ( − x ) 2 + f ( x ) − f ( − x ) 2 = f even + f odd f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}=f_{\text{even}}+f_{\text{odd}} f(x)=2f(x)+f(−x)+2f(x)−f(−x)=feven+fodd
所以同时需要sin(x),cos(x)。
2.3 保证组合出来周期为T
之前说了, f ( x ) f(x) f(x)是周期为 T T T的函数,我们怎么保证组合出来的函数周期依然为 T T T呢?
比如下面这个函数的周期为 2 π 2\pi 2π:
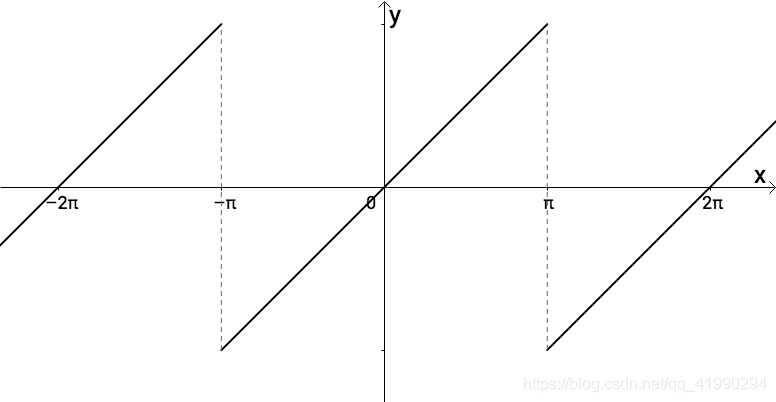
很显然, s i n ( x ) sin(x) sin(x)的周期也是 2 π 2\pi 2π:
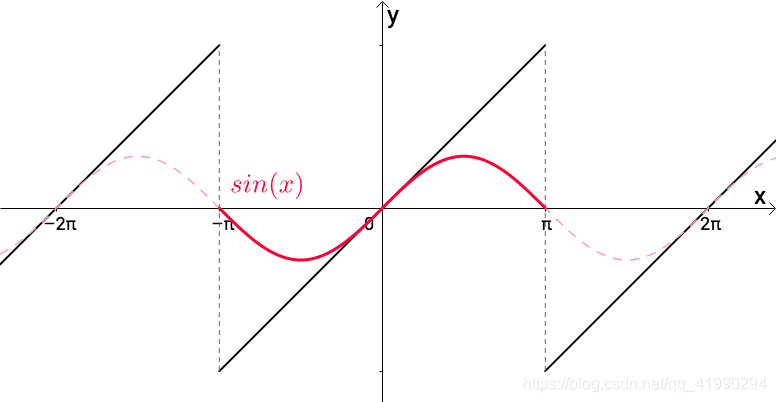
s i n ( 2 x ) sin(2x) sin(2x)的周期也是 2 π 2\pi 2π,虽然最小周期是 π \pi π:

很显然, s i n ( n x ) , n ∈ N sin(nx),n\in\mathbb{N} sin(nx),n∈N的周期都是 2 π 2\pi 2π:
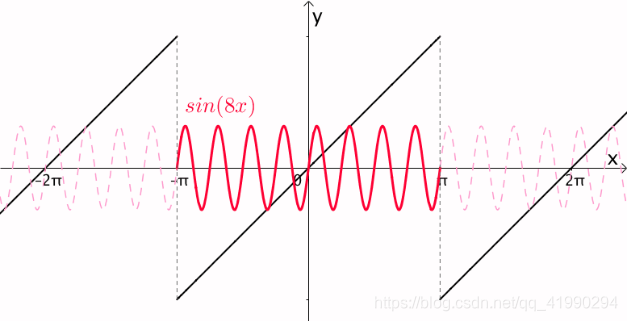
更一般的,如果 f ( x ) f(x) f(x)的周期为 T T T,那么:
s i n ( 2 π n T x ) c o s ( 2 π n T x ) , n ∈ N sin({\frac{2\pi n}{T}x})\quad cos({\frac{2\pi n}{T}x}),n\in\mathbb{N} sin(T2πnx)cos(T2πnx),n∈N
这些函数的周期都为 T T T。
将这些函数进行加减,就保证了得到的函数的周期也为 T T T。
2.4 调整振幅
现在我们有一堆周期为 2 π 2\pi 2π的函数了,比如说 s i n ( x ) , s i n ( 2 x ) , s i n ( 3 x ) , s i n ( 4 x ) , s i n ( 5 x ) sin(x),sin(2x),sin(3x),sin(4x),sin(5x) sin(x),sin(2x),sin(3x),sin(4x),sin(5x):

通过调整振幅可以让它们慢慢接近目标函数,比如 s i n ( x ) sin(x) sin(x)看起来处处都比目标函数低一些:

把它的振幅增加一倍:

2 s i n ( x ) 2sin(x) 2sin(x)有的地方超出去了,从周期为 2 π 2\pi 2π的函数中选择一个,减去一点:
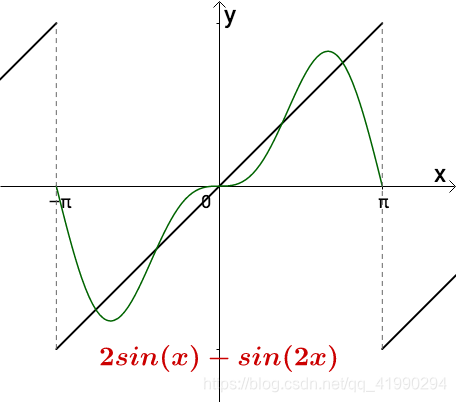
调整振幅,加加减减,我们可以慢慢接近目标函数:
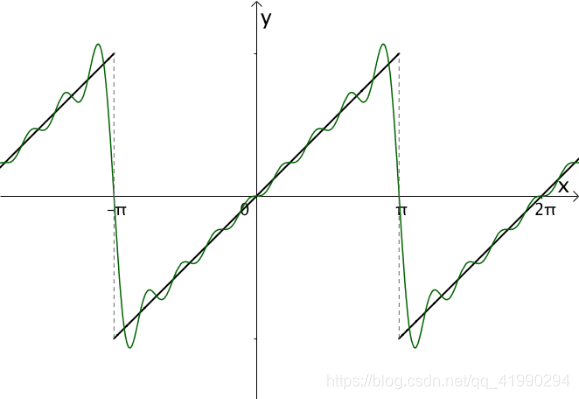
2.5 小结
综上,构造出来的三角函数之和大概类似下面的样子:

这样就符合之前的分析:
\quad\quad 1.有常数项
\quad\quad 2.奇函数和偶函数可以组合出任意函数
\quad\quad 3.周期为 T T T
\quad\quad 4.调整振幅,逼近原函数
之前的分析还比较简单,后面开始有点难度了。即怎么确定这三个系数:
C a n b n C\quad a_n\quad b_n Canbn
3 s i n ( x ) sin(x) sin(x)的另外一种表示方法
直接不好确定,要迂回一下,先稍微介绍一下什么是: e i ω t e^{i\omega t} eiωt?
3.1 e i ω t e^{i\omega t} eiωt
看到类似于 e i θ e^{i\theta} eiθ这种就应该想到复平面上的一个夹角为 θ \theta θ的向量:

那么当 θ \theta θ不再是常数,而是代表时间的变量 t t t的时候:
e i θ → e i t e^{i\theta}\to e^{i{\color{red}t}} eiθ→eit
随着时间 t t t的流逝,从0开始增长,这个向量就会旋转起来, 2 π 2\pi 2π秒会旋转一圈,也就是 T = 2 π T=2\pi T=2π:

3.2 通过e^{i\omega t}表示sin(t)
根据欧拉公式,有:
e i t = c o s ( t ) + i s i n ( t ) e^{it}=cos(t)+isin(t) eit=cos(t)+isin(t)
所以,在时间t轴上,把 e i t e^{it} eit向量的虚部(也就是纵坐标)记录下来,得到的就是 s i n ( t ) sin(t) sin(t):
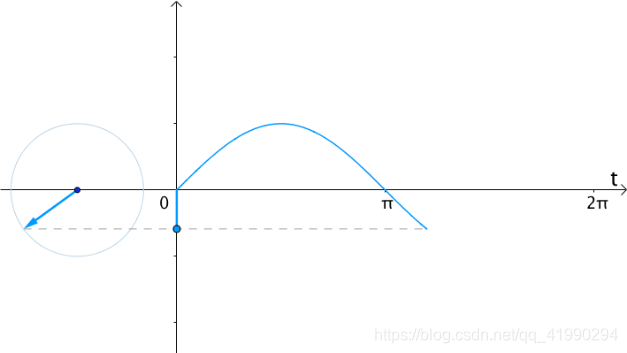
在时间 t t t轴上,把 e i 2 t e^{i2t} ei2t向量的虚部记录下来,得到的就是 s i n ( 2 t ) sin(2t) sin(2t):
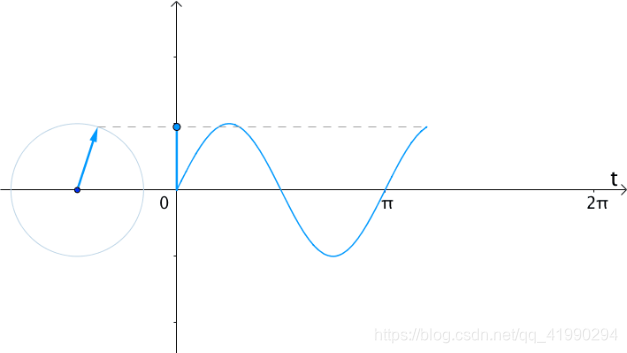
如果在时间 t t t轴上,把 e i t e^{it} eit的实部(横坐标)记录下来,得到的就是 c o s ( t ) cos(t) cos(t)的曲线:
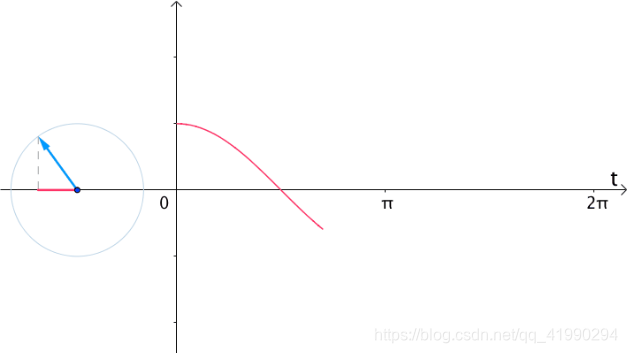
更一般的我们认为,我们具有两种看待 s i n ( x ) , c o s ( x ) sin(x),cos(x) sin(x),cos(x)的角度:
e i ω t ⟺ { s i n ( ω t ) c o s ( ω t ) e^{i\omega t}\iff \begin{cases}sin(\omega t)\\cos(\omega t)\end{cases} eiωt⟺{sin(ωt)cos(ωt)
这两种角度,一个可以观察到旋转的频率,所以称为频域;一个可以看到流逝的时间,所以称为时域:
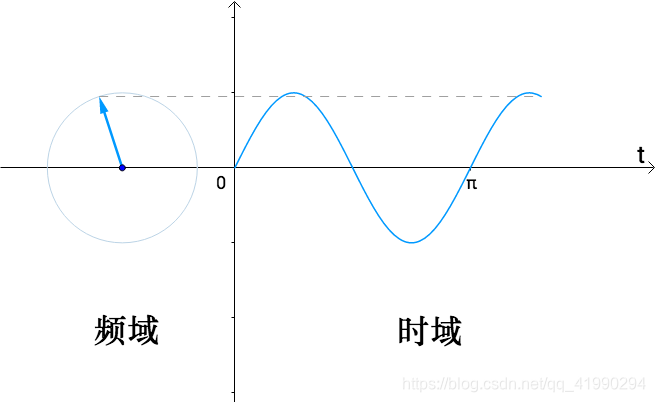
4 通过频域来求系数
4.1 函数是线性组合
假设有这么个函数:
g ( x ) = s i n ( x ) + s i n ( 2 x ) g(x)=sin(x)+sin(2x) g(x)=sin(x)+sin(2x)
是一个 T = 2 π T=2\pi T=2π的函数:
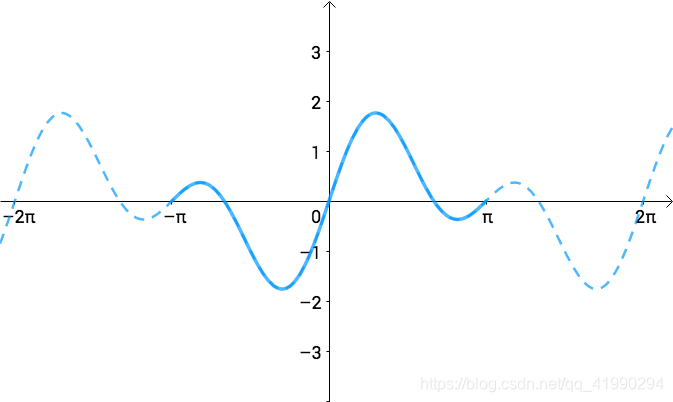
如果转到频域去,那么它们是下面这个复数函数的虚部:
e i t + e i 2 t e^{it}+e^{i2t} eit+ei2t
先看看 e i θ + e i 2 θ e^{i\theta}+e^{i2\theta} eiθ+ei2θ,其中 θ \theta θ是常数,很显然这是两个向量之和:

现在让它们动起来,把 θ \theta θ变成流逝的时间 t t t,并且把虚部记录下来:
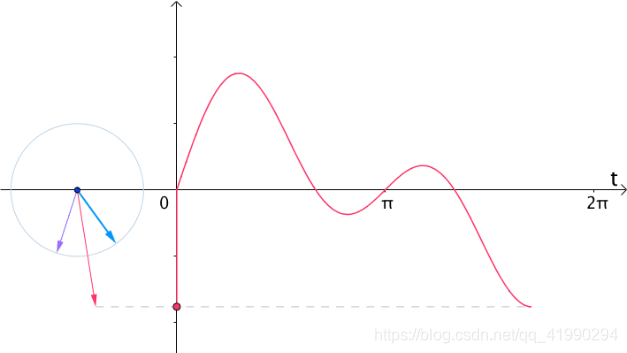
我们令:
G ( t ) = e i t + e i 2 t G(t)=e^{it}+e^{i2t} G(t)=eit+ei2t
这里用大写的 G G G来表示复数函数。
刚才看到了, e i t e^{it} eit和 e i 2 t e^{i2t} ei2t都是向量,所以上式可以写作:
G ( t ) ⃗ = e i t ⃗ + e i 2 t ⃗ \vec{G(t)}=\vec{e^{it}}+\vec{e^{i2t}} G(t)=eit+ei2t
这里就是理解的重点了,从线性代数的角度:
\quad\quad 1. e i t e^{it} eit和 e i 2 t e^{i2t} ei2t是基(可以参考无限维的希尔伯特空间)
\quad\quad 2. G ( t ) G(t) G(t)是基 e i t e^{it} eit, e i 2 t e^{i2t} ei2t的线性组合
g ( t ) g(t) g(t)是 G ( t ) G(t) G(t)的虚部,所以取虚部,很容易得到:
g ( t ) ⃗ = s i n ( t ) ⃗ + s i n ( 2 t ) ⃗ \vec{g(t)}=\vec{sin(t)}+\vec{sin(2t)} g(t)=sin(t)+sin(2t)
即 g ( t ) g(t) g(t)是基 s i n ( t ) , s i n ( 2 t ) sin(t),sin(2t) sin(t),sin(2t)的线性组合。
那么 s i n ( t ) , s i n ( 2 t ) sin(t),sin(2t) sin(t),sin(2t)的系数,实际上是 g ( t ) g(t) g(t)在基 s i n ( t ) , s i n ( 2 t ) sin(t),sin(2t) sin(t),sin(2t)下的坐标了。
4.2 如何求正交基的坐标
有了这个结论之后,我们如何求坐标?
我们来看个例子,假设:
w ⃗ = 2 u ⃗ + 3 v ⃗ \vec{w_{}}=2\vec{u_{}}+3\vec{v_{}} w=2u+3v
其中 u ⃗ = ( 1 1 ) , v ⃗ = ( − 1 1 ) \vec{u_{}}=\begin{pmatrix}1\\1\end{pmatrix},\vec{v_{}}=\begin{pmatrix}-1\\1\end{pmatrix} u=(11),v=(−11)
通过点积
u ⃗ ⋅ v ⃗ = 0 \vec{u_{}}\cdot \vec{v_{}}=0 u⋅v=0
可知这两个向量正交,是正交基。图示如下:
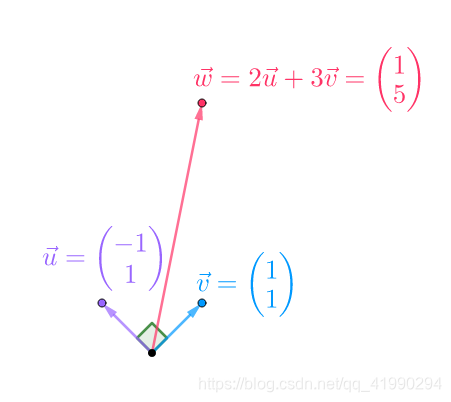
通过点积可以算出 u ⃗ \vec{u_{}} u的系数(对于正交基才可以这么做):
w ⃗ ⋅ u ⃗ u ⃗ ⋅ u ⃗ = ( 1 , 5 ) ⋅ ( − 1 , 1 ) ( − 1 , 1 ) ⋅ ( − 1 , 1 ) = 2 \frac{\vec{w_{}}\cdot \vec{u_{}}}{\vec{u_{}}\cdot \vec{u_{}}}=\frac{(1,5)\cdot(-1,1)}{(-1,1)\cdot(-1,1)}=2 u⋅uw⋅u=(−1,1)⋅(−1,1)(1,5)⋅(−1,1)=2
4.3 如何求sin(nt)基下的坐标
在这里抛出一个结论(可以参考无限维的希尔伯特空间),函数向量的点积是这么定义的:
f ( x ) ⃗ ⋅ g ( x ) ⃗ = ∫ 0 T f ( x ) g ( x ) d x \vec{f(x)}\cdot\vec{g(x)}=\int_{0}^{T}f(x)g(x)dx f(x)⋅g(x)=∫0Tf(x)g(x)dx
\quad\quad 其中, f ( x ) f(x) f(x)是函数向量, g ( x ) g(x) g(x)是基, T T T是 f ( x ) f(x) f(x)的周期。
那么对于:
g ( x ) = s i n ( x ) + s i n ( 2 x ) g(x)=sin(x)+sin(2x) g(x)=sin(x)+sin(2x)
\quad\quad 其中, g ( x ) g(x) g(x)是向量, s i n ( t ) , s i n ( 2 t ) sin(t),sin(2t) sin(t),sin(2t)是基,周期 T = 2 π T=2\pi T=2π。
根据刚才内积的定义:
s i n ( t ) ⃗ ⋅ s i n ( 2 t ) ⃗ = ∫ 0 2 π s i n ( t ) s i n ( 2 t ) d t = 0 \vec{sin(t)}\cdot\vec{sin(2t)}=\int_{0}^{2\pi}sin(t)sin(2t)dt=0 sin(t)⋅sin(2t)=∫02πsin(t)sin(2t)dt=0
所以是正交基,那么根据刚才的分析,可以这么求坐标:
g ⃗ ⋅ s i n ( t ) ⃗ s i n ( t ) ⃗ ⋅ s i n ( t ) ⃗ = ∫ 0 2 π g ( x ) s i n ( x ) d x ∫ 0 2 π s i n 2 ( x ) d x = 1 \frac{\vec{g_{}}\cdot \vec{sin(t)}}{\vec{sin(t)}\cdot \vec{sin(t)}}=\frac{\int_{0}^{2\pi}g(x)sin(x)dx}{\int_{0}^{2\pi}sin^2(x)dx}=1 sin(t)⋅sin(t)g⋅sin(t)=∫02πsin2(x)dx∫02πg(x)sin(x)dx=1
4.4 更一般的
对于我们之前的假设,其中 f ( x ) f(x) f(x)周期为 T T T:
f ( x ) = C + ∑ n = 1 ∞ ( a n c o s ( 2 π n T x ) + b n s i n ( 2 π n T x ) ) , C ∈ R \displaystyle f(x)=C+\sum _{{n=1}}^{\infty}\left(a_{n}cos({\frac{2\pi n}{T}x})+b_{n}sin({\frac{2\pi n}{T}x})\right),C\in\mathbb{R} f(x)=C+n=1∑∞(ancos(T2πnx)+bnsin(T2πnx)),C∈R
可以改写为这样:
f ( x ) = C ⋅ 1 + ∑ n = 1 ∞ ( a n c o s ( 2 π n T x ) + b n s i n ( 2 π n T x ) ) , C ∈ R \displaystyle f(x)=C\cdot 1+\sum _{{n=1}}^{\infty}\left(a_{n}cos({\frac{2\pi n}{T}x})+b_{n}sin({\frac{2\pi n}{T}x})\right),C\in\mathbb{R} f(x)=C⋅1+n=1∑∞(ancos(T2πnx)+bnsin(T2πnx)),C∈R
也就是说向量 f ( x ) f(x) f(x)的基为:
{ 1 , c o s ( 2 π n T x ) , s i n ( 2 π n T x ) } \{1,cos({\frac{2\pi n}{T}x}),sin({\frac{2\pi n}{T}x})\} {1,cos(T2πnx),sin(T2πnx)}
是的,1也是基。
那么可以得到:
a n = ∫ 0 T f ( x ) c o s ( 2 π n T x ) d x ∫ 0 T c o s 2 ( 2 π n T x ) d x = 2 T ∫ 0 T f ( x ) c o s ( 2 π n T x ) d x a_n=\frac{\int_{0}^{T}f(x)cos({\frac{2\pi n}{T}x})dx}{\int_{0}^{T}cos^2({\frac{2\pi n}{T}x})dx}=\frac{2}{T}\int_{0}^{T}f(x)cos({\frac{2\pi n}{T}x})dx an=∫0Tcos2(T2πnx)dx∫0Tf(x)cos(T2πnx)dx=T2∫0Tf(x)cos(T2πnx)dx
b n = ∫ 0 T f ( x ) s i n ( 2 π n T x ) d x ∫ 0 T s i n 2 ( 2 π n T x ) d x = 2 T ∫ 0 T f ( x ) s i n ( 2 π n T x ) d x b_n=\frac{\int_{0}^{T}f(x)sin({\frac{2\pi n}{T}x})dx}{\int_{0}^{T}sin^2({\frac{2\pi n}{T}x})dx}=\frac{2}{T}\int_{0}^{T}f(x)sin({\frac{2\pi n}{T}x})dx bn=∫0Tsin2(T2πnx)dx∫0Tf(x)sin(T2πnx)dx=T2∫0Tf(x)sin(T2πnx)dx
C也可以通过点积来表示,最终我们得到:
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos ( 2 π n x T ) + b n sin ( 2 π n x T ) ) \displaystyle f(x)={\frac{a_{0}}{2}}+\sum _{{n=1}}^{\infty}\left(a_{n}\cos({\tfrac {2\pi nx}{T}})+b_{n}\sin({\tfrac {2\pi nx}{T}})\right) f(x)=2a0+n=1∑∞(ancos(T2πnx)+bnsin(T2πnx))
其中:
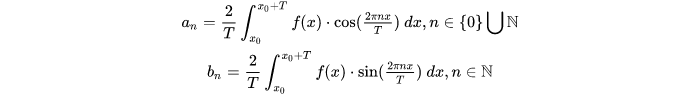
这篇关于如何理解傅立叶级数公式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







