【数据结构】数组和字符串（五）：特殊矩阵的压缩存储：稀疏矩阵——压缩稀疏行（CSR）

2023-10-28 20:01
文章标签 数组 数据结构 字符串 特殊 存储 压缩 矩阵 csr 稀疏

本文主要是介绍【数据结构】数组和字符串（五）：特殊矩阵的压缩存储：稀疏矩阵——压缩稀疏行（CSR），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 4.2.1 矩阵的数组表示
  • 4.2.2 特殊矩阵的压缩存储
    • a. 对角矩阵的压缩存储
    • b~c. 三角、对称矩阵的压缩存储
    • d. 稀疏矩阵的压缩存储——三元组表
    • e. 压缩稀疏行（Compressed Sparse Row，CSR）矩阵
      • 结构体
      • 创建CSR矩阵
      • 元素设置
      • 初始化
      • 打印矩阵
      • 销毁CSR矩阵
      • 主函数
      • 代码整合

4.2.1 矩阵的数组表示

【数据结构】数组和字符串（一）：矩阵的数组表示

4.2.2 特殊矩阵的压缩存储

  矩阵是以按行优先次序将所有矩阵元素存放在一个一维数组中。但是对于特殊矩阵，如对称矩阵、三角矩阵、对角矩阵和稀疏矩阵等, 如果用这种方式存储，会出现大量存储空间存放重复信息或零元素的情况，这样会造成很大的空间浪费。为节约存储空间和算法（程序）运行时间，通常会采用压缩存储的方法。

  • 对角矩阵：指除了主对角线以外的元素都为零的矩阵，即对 任意 i ≠ j (1≤ i , j ≤n)，都有M(i, j)=0。由于只有主对角线上有非零元素，只需存储主对角线上的元素即可。
  • 三角矩阵：指上三角或下三角的元素都为零的矩阵。同样地，只需存储其中一部分非零元素，可以节省存储空间。
  • 对称矩阵：指矩阵中的元素关于主对角线对称的矩阵。由于对称矩阵的非零元素有一定的规律，可以只存储其中一部分元素，从而减少存储空间。
  • 稀疏矩阵：指大部分元素为零的矩阵。传统的按行优先次序存储方法会浪费大量空间来存储零元素，因此采用压缩存储的方法更为合适。常见的压缩存储方法有：压缩稠密行（CSR）、压缩稠密列（CSC）、坐标列表（COO）等。

a. 对角矩阵的压缩存储

【数据结构】数组和字符串（二）：特殊矩阵的压缩存储：对角矩阵——一维数组

b~c. 三角、对称矩阵的压缩存储

【数据结构】数组和字符串（三）：特殊矩阵的压缩存储：三角矩阵、对称矩阵——一维数组

d. 稀疏矩阵的压缩存储——三元组表

【数据结构】数组和字符串（四）：特殊矩阵的压缩存储：稀疏矩阵——三元组表

e. 压缩稀疏行（Compressed Sparse Row，CSR）矩阵

  压缩稀疏行（Compressed Sparse Row，CSR）是一种常用的稀疏矩阵存储格式。CSR存储格式通过压缩非零元素的行指针和列索引，以及存储非零元素的值，来有效地表示稀疏矩阵。它包含以下几个关键组成部分：

  • row_ptr（行指针数组）：它是一个长度为rows + 1的数组，用于存储每一行在col_indices和elements数组中的起始索引位置。row_ptr[i]表示第i行的元素在col_indices和elements数组中的起始位置，而row_ptr[i+1] - row_ptr[i]表示第i行的非零元素个数。
  • col_indices（列索引数组）：它是一个长度为num_elements的数组，用于存储每个非零元素对应的列索引。col_indices[i]表示第i个非零元素所在的列索引。
  • elements（元素数组）：它是一个长度为num_elements的数组，用于存储每个非零元素的值。elements[i]表示第i个非零元素的值。

  CSR存储格式的主要优点是有效地压缩了稀疏矩阵的存储空间，只存储非零元素及其对应的行和列信息。此外，CSR格式还支持高效的稀疏矩阵向量乘法和稀疏矩阵乘法等操作。

结构体

typedef struct {int row;int col;int value;
} Element;typedef struct {int rows;int cols;int num_elements;Element* elements;int* row_ptr;int* col_indices;
} CSRMatrix;

  • Element 结构体表示矩阵中的一个元素，包含三个成员变量：row（行索引）、col（列索引）和 value（元素值）。

  • CSRMatrix 结构体表示一个CSR矩阵，包含了矩阵的行数 rows、列数 cols、非零元素的个数 num_elements，以及三个指针成员变量 elements、row_ptr 和 col_indices。

创建CSR矩阵

CSRMatrix createCSRMatrix(int rows, int cols, int num_elements) {CSRMatrix matrix;matrix.rows = rows;matrix.cols = cols;matrix.num_elements = num_elements;matrix.elements = (Element*)malloc(num_elements * sizeof(Element));matrix.row_ptr = (int*)malloc((rows + 1) * sizeof(int));matrix.col_indices = (int*)malloc(num_elements * sizeof(int));return matrix;
}
  • createCSRMatrix 函数用于创建一个CSR矩阵。
  • 接受矩阵的行数、列数和非零元素的个数作为参数，并返回创建的CSR矩阵。
  • 在函数内部，通过动态内存分配分别为 elements、row_ptr 和 col_indices 分配内存空间，并将 row_ptr 数组的所有元素初始化为0，最后返回创建的矩阵。

元素设置

void setElement(CSRMatrix* matrix, int row, int col, int value) {if (row < 0 || row >= matrix->rows) {printf("Invalid row index.\n");return;}int index = matrix->row_ptr[row];matrix->elements[index].row = row;matrix->elements[index].col = col;matrix->elements[index].value = value;matrix->col_indices[index] = col;matrix->row_ptr[row]++;  // 递增索引值
}

  setElement 函数可用于设置（修改）CSR矩阵中某个位置的元素值。

  • 接受一个指向CSR矩阵的指针 matrix，以及要设置的元素的行索引、列索引和值作为参数。
  • 在函数内部，首先检查行索引是否有效，如果无效则打印错误信息并返回。
  • 然后，根据行索引找到对应行的起始位置，将元素的行索引、列索引和值分别赋给对应的矩阵元素，并更新 col_indices 数组和 row_ptr 数组中的值。

初始化

void initializeCSRMatrix(CSRMatrix* matrix, int* values, int* row_indices, int* col_indices, int num_elements) {for (int i = 0; i < num_elements; i++) {matrix->elements[i].value = values[i];matrix->elements[i].row = row_indices[i];matrix->elements[i].col = col_indices[i];matrix->col_indices[i] = col_indices[i];matrix->row_ptr[row_indices[i]]++;}int sum = 0;for (int i = 0; i <= matrix->rows; i++) {int temp = matrix->row_ptr[i];matrix->row_ptr[i] = sum;sum += temp;}
}

  initializeCSRMatrix 函数用于初始化CSR矩阵的数据。

  • 接受一个指向CSR矩阵的指针 matrix，以及包含非零元素的值、行索引和列索引的数组，以及非零元素的个数作为参数。
  • 通过遍历非零元素数组，将值、行索引和列索引分别赋给对应的矩阵元素，并更新 col_indices 数组和 row_ptr 数组中的值。row_ptr 数组的每个元素表示对应行的非零元素在 elements 数组中的起始位置，通过累加非零元素的个数来计算每行的结束位置。

打印矩阵

void printCSRMatrix(CSRMatrix matrix) {printf("CSR Matrix:\n");printf("Rows: %d, Cols: %d, Num Elements: %d\n", matrix.rows, matrix.cols, matrix.num_elements);printf("Values: ");for (int i = 0; i < matrix.num_elements; i++) {printf("%d ", matrix.elements[i].value);}printf("\n");printf("Row Pointer: ");for (int i = 0; i <= matrix.rows; i++) {printf("%d ", matrix.row_ptr[i]);}printf("\n");printf("Column Indices: ");for (int i = 0; i < matrix.num_elements; i++) {printf("%d ", matrix.col_indices[i]);}printf("\n");
}
void printMatrixForm(CSRMatrix matrix) {printf("Matrix Form:\n");for (int i = 0; i < matrix.rows; i++) {for (int j = 0; j < matrix.cols; j++) {int value = 0;for (int k = matrix.row_ptr[i]; k < matrix.row_ptr[i + 1]; k++) {if (matrix.elements[k].col == j) {value = matrix.elements[k].value;break;}}printf("%d ", value);}printf("\n");}
}
  • printCSRMatrix 函数用于打印CSR矩阵的信息：它接受一个CSR矩阵作为参数，并打印矩阵的行数、列数、非零元素的个数以及 elements、row_ptr 和 col_indices 数组的内容。
  • printMatrixForm 函数用于以矩阵形式打印CSR矩阵。它接受一个CSR矩阵作为参数，并按矩阵的行数和列数遍历矩阵元素，通过遍历 row_ptr 数组和 col_indices 数组来获取每个位置的元素值，并打印出矩阵的形式。

销毁CSR矩阵

void destroyCSRMatrix(CSRMatrix* matrix) {free(matrix->elements);free(matrix->row_ptr);free(matrix->col_indices);matrix->elements = NULL;matrix->row_ptr = NULL;matrix->col_indices = NULL;
}

主函数

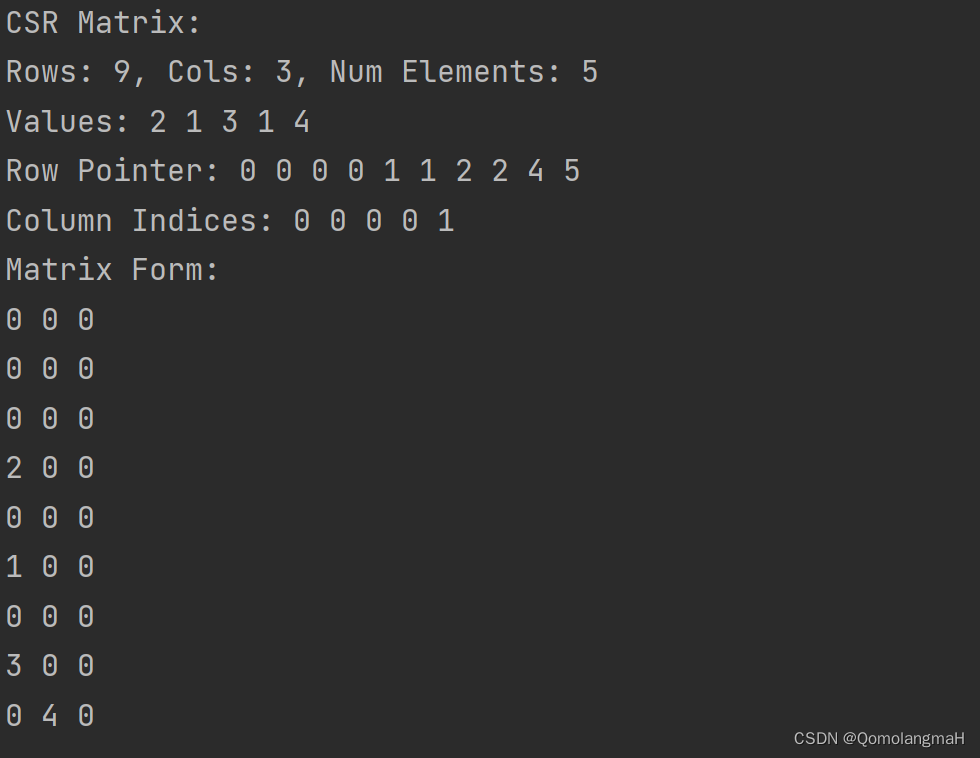
int main() {int rows = 9;int cols = 3;int num_elements = 5;CSRMatrix matrix = createCSRMatrix(rows, cols, num_elements);int col_indices[] = {0, 0, 0, 0, 1};int row_indices[] = {3, 5, 7, 8, 7};int values[] =      {2, 1, 3, 1, 4};initializeCSRMatrix(&matrix, values, row_indices, col_indices, num_elements);printCSRMatrix(matrix);printMatrixForm(matrix);destroyCSRMatrix(&matrix);return 0;
}

在这里插入图片描述

代码整合

#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef struct {int row;int col;int value;
} Element;typedef struct {int rows;int cols;int num_elements;Element* elements;int* row_ptr;int* col_indices;
} CSRMatrix;CSRMatrix createCSRMatrix(int rows, int cols, int num_elements) {CSRMatrix matrix;matrix.rows = rows;matrix.cols = cols;matrix.num_elements = num_elements;matrix.elements = (Element*)malloc(num_elements * sizeof(Element));matrix.row_ptr = (int*)malloc((rows + 1) * sizeof(int));matrix.col_indices = (int*)malloc(num_elements * sizeof(int));memset(matrix.row_ptr, 0, (rows + 1) * sizeof(int));return matrix;
}
void initializeCSRMatrix(CSRMatrix* matrix, int* values, int* row_indices, int* col_indices, int num_elements) {for (int i = 0; i < num_elements; i++) {matrix->elements[i].value = values[i];matrix->elements[i].row = row_indices[i];matrix->elements[i].col = col_indices[i];matrix->col_indices[i] = col_indices[i];matrix->row_ptr[row_indices[i]]++;}int sum = 0;for (int i = 0; i <= matrix->rows; i++) {int temp = matrix->row_ptr[i];matrix->row_ptr[i] = sum;sum += temp;}
}void setElement(CSRMatrix* matrix, int row, int col, int value) {if (row < 0 || row >= matrix->rows) {printf("Invalid row index.\n");return;}int index = matrix->row_ptr[row];matrix->elements[index].row = row;matrix->elements[index].col = col;matrix->elements[index].value = value;matrix->col_indices[index] = col;matrix->row_ptr[row]++;  // 递增索引值
}void printCSRMatrix(CSRMatrix matrix) {printf("CSR Matrix:\n");printf("Rows: %d, Cols: %d, Num Elements: %d\n", matrix.rows, matrix.cols, matrix.num_elements);printf("Values: ");for (int i = 0; i < matrix.num_elements; i++) {printf("%d ", matrix.elements[i].value);}printf("\n");printf("Row Pointer: ");for (int i = 0; i <= matrix.rows; i++) {printf("%d ", matrix.row_ptr[i]);}printf("\n");printf("Column Indices: ");for (int i = 0; i < matrix.num_elements; i++) {printf("%d ", matrix.col_indices[i]);}printf("\n");
}
void printMatrixForm(CSRMatrix matrix) {printf("Matrix Form:\n");for (int i = 0; i < matrix.rows; i++) {for (int j = 0; j < matrix.cols; j++) {int value = 0;for (int k = matrix.row_ptr[i]; k < matrix.row_ptr[i + 1]; k++) {if (matrix.elements[k].col == j) {value = matrix.elements[k].value;break;}}printf("%d ", value);}printf("\n");}
}void destroyCSRMatrix(CSRMatrix* matrix) {free(matrix->elements);free(matrix->row_ptr);free(matrix->col_indices);matrix->elements = NULL;matrix->row_ptr = NULL;matrix->col_indices = NULL;
}int main() {int rows = 9;int cols = 3;int num_elements = 5;CSRMatrix matrix = createCSRMatrix(rows, cols, num_elements);int col_indices[] = {0, 0, 0, 0, 1};int row_indices[] = {3, 5, 7, 8, 7};int values[] =      {2, 1, 3, 1, 4};initializeCSRMatrix(&matrix, values, row_indices, col_indices, num_elements);printCSRMatrix(matrix);printMatrixForm(matrix);destroyCSRMatrix(&matrix);return 0;
}

这篇关于【数据结构】数组和字符串（五）：特殊矩阵的压缩存储：稀疏矩阵——压缩稀疏行（CSR）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/295610。

相关文章

异构存储（冷热数据分离）

异构存储（冷热数据分离）

异构存储主要解决不同的数据，存储在不同类型的硬盘中，达到最佳性能的问题。 异构存储Shell操作 （1）查看当前有哪些存储策略可以用 [lytfly@hadoop102 hadoop-3.1.4]$ hdfs storagepolicies -listPolicies （2）为指定路径（数据存储目录）设置指定的存储策略 hdfs storagepolicies -setStoragePo
阅读更多...
HDFS—存储优化（纠删码）

HDFS—存储优化（纠删码）

纠删码原理 HDFS 默认情况下，一个文件有3个副本，这样提高了数据的可靠性，但也带来了2倍的冗余开销。 Hadoop3.x 引入了纠删码，采用计算的方式，可以节省约50％左右的存储空间。 此种方式节约了空间，但是会增加 cpu 的计算。 纠删码策略是给具体一个路径设置。所有往此路径下存储的文件，都会执行此策略。 默认只开启对 RS-6-3-1024k
阅读更多...
hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

利用康拓展开将一个排列映射成一个自然数，然后就变成了普通的广搜题。 #include<iostream>#include<algorithm>#include<string>#include<stack>#include<queue>#include<map>#include<stdio.h>#include<stdlib.h>#include<ctype.h>#inclu
阅读更多...
hdu1565（状态压缩）

hdu1565（状态压缩）

本人第一道ac的状态压缩dp，这题的数据非常水，很容易过 题意：在n*n的矩阵中选数字使得不存在任意两个数字相邻，求最大值 解题思路： 一、因为在1<<20中有很多状态是无效的，所以第一步是选择有效状态，存到cnt[]数组中 二、dp[i][j]表示到第i行的状态cnt[j]所能得到的最大值，状态转移方程dp[i][j] = max(dp[i][j],dp[i-1][k]) ,其中k满足c
阅读更多...
hdu2241（二分+合并数组）

hdu2241（二分+合并数组）

题意：判断是否存在a+b+c = x，a，b，c分别属于集合A,B,C 如果用暴力会超时，所以这里用到了数组合并，将b,c数组合并成d，d数组存的是b，c数组元素的和，然后对d数组进行二分就可以了 代码如下（附注释）： #include<iostream>#include<algorithm>#include<cstring>#include<stack>#include<que
阅读更多...
【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
hdu 1166 敌兵布阵（树状数组 or 线段树）

hdu 1166 敌兵布阵（树状数组 or 线段树）

题意是求一个线段的和，在线段上可以进行加减的修改。 树状数组的模板题。 代码： #include <stdio.h>#include <string.h>const int maxn = 50000 + 1;int c[maxn];int n;int lowbit(int x){return x & -x;}void add(int x, int num){while
阅读更多...
6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

上篇：6.1.数据结构-c/c++模拟实现堆上篇（向下，上调整算法，建堆，增删数据）-CSDN博客 本章重点 1.使用堆来完成堆排序 2.使用堆解决TopK问题 目录 一.堆排序 1.1 思路 1.2 代码 1.3 简单测试 二.TopK问题 2.1 思路(求最小)： 2.2 C语言代码（手写堆） 2.3 C++代码（使用优先级队列 priority_queue）
阅读更多...
hdu 4565 推倒公式+矩阵快速幂

hdu 4565 推倒公式+矩阵快速幂

题意 求下式的值： Sn=⌈ (a+b√)n⌉%m S_n = \lceil\ (a + \sqrt{b}) ^ n \rceil\% m 其中： 0<a,m<215 0< a, m < 2^{15} 0<b,n<231 0 < b, n < 2^{31} (a−1)2<b<a2 (a-1)^2< b < a^2 解析 令： An=(a+b√)n A_n = (a +
阅读更多...
BUUCTF（34）特殊的 BASE64

BUUCTF（34）特殊的 BASE64

使用pycharm时，如果想把代码撤销到之前的状态可以用 Ctrl+z 如果不小心撤销多了，可以用 Ctrl+Shift+Z 还原， 别傻傻的重新敲了 BUUCTF在线评测 (buuoj.cn) 查看字符串，想到base64的变表 这里用的c++的标准程序库中的string，头文件是#include<string> 这是base64的加密函数 std::string
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2