本文主要是介绍一种基于bayer型模式的双边自适应滤波器,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
介绍一种基于bayer型模式的双边自适应滤波器。由于此时仅需对二维灰度图像进行滤波处理,它的硬件资源消耗可以减小为前者的三分之一。双边自适应滤波器不仅对各类噪声有良好的滤除能力,还能使图像中的细节得到很好的保留。
在bayer型中,每个像素点的数据值只有一个,可能为RGB中的任何一个,对于G点,它的4邻域内没有G点的存在,对于R点和B点来说,甚至在它们的8领域内也没有相同颜色的点的存在。要对该点滤波,需要利用数量不多的相同颜色点的值。传感器在感光时具有空间相关性,即正常情况下图像在局部区域都是平滑过渡的,不会在某个孤立的点处产生突然的巨大的跳变。因此到需要滤波点的距离越近的点,它们之间的数值彼此应当更加接近,它们之间的相关性就越高。
说明了当对具有R值的点滤波时的情况。在该图中,如要对R13进行滤波处理,需要得到以R13为中心的一个5×5的邻域。在这里同为R点的坐标分别为R1、R3、R5、R1l、R13、R15、R21、1123、R25,只有它们与中心点R13具有相关性,参加滤波过程的计算。在这些点中,R3、R11、R15、R23距离中心点R13最近,与R13的空间相关性最高,在滤波过程中做出的贡献最大。而R1、R5、R21、R25则距离R13最远,空间相关性低,在滤波过程中做出的贡献相对较小。

根据空间相关性,我们可以得到一个5x5的矩阵,该矩阵能够很好的反映出这种相关性。

在双边滤波的过程中,不仅需要像素之间的空间相关性,还需要它们彼此之间的数值相关性。对于同为R的点,当它们与中心点之间数值相差越小,说明彼此之间的相关程度越高,在滤波过程中就越重要。但是当数值之差超过一定的界限后,就说明该点的值与中心点存在过大的差异,说明两者之间没有相关性。
计算数值相关性矩阵的伪代码如下:

在上述的伪代码中,data、C_distanee、C weight都是5X 5矩阵。C_distance代表(i,j)处的数值和中心点之间数值的差异,C weight代表(i,j)处与中心点数值相关性的高低。此处选用了线性函数来量化C_Distanc、C_weight之间的关系(如图3.7所示),其中b的取值依据对于目标相关性的情况而取定,在此我们选择了32(5bit),以方便最后的硬件实现,同时节约硬件资源。

由此可以得到一个关于C_weight的5X5的矩阵。最后可以通过Distance_r,C_weight得到滤波所需要的5×5掩模Mr,用此掩模对图3.7中的邻域滤波,利用下式计算,得到去噪后的R值。

当对具有B值的点滤波时的5X 5邻域如图3.8所示。此时对于B点的邻域和R点的邻域基本一致,它们的的滤波方式也很相似,只是将前面所提到的R值用B值来代替即可。

在bayer型中。G点的数量是R点或B点数量的两倍,它的邻域存在两种不同的情况,如图3.9所示,但是这种不同仅仅是R点和B点排列顺序的不同,它们对于G点滤波计算时没有任何的影响。

在对G13点滤波时将会有G1、G3、G5、G7、G9、G11、G15、G17、G19、G21、G23、G25等十二个点参加计算。其中G7、G9、G17、G19距离中心点的最近,它们之问的空间相关性最高,在滤波过程中作出的贡献最大。(G3、Gll、G15、G23距离中心点稍远,它们之间的空问相关性次之,在滤波过程中作出的贡献较小。G1、G5、G21、G25距离中心点最远,它们之间的空间相关性最小,如果要节省硬件资源,在计算过程中甚至可以不予考虑。
根据空间相关性,我们可以得到一个5X5的矩阵,该矩阵能够很好的反映出对于G点的这种相关性。

在双边滤波的过程中,G点的滤波也需要考虑它们彼此之间的数值相关性。在图3.9中,对于同为G的点,当它们与中心点之问数值相差越小,说明彼此之间的相关程度越高,在滤波过程中就越重要。这一点与R点滤波过程中的数值相关性是一致的。
由此可以得到一个关于G点的C_weight 5X5的矩阵。最后可以通过Distance g×C weight得到滤波所需要的5X5掩模Mg,用此掩模对图3.9中的邻域滤波,利用下式计算得到去噪后的G值。
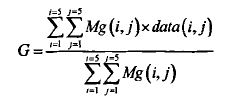
至此,对于整幅图像中的所有情况的去噪过程就完成了。为了减少硬件的开支,Distance矩阵可以在计算开始之前,就把它作为一个常数值在硬件中固化好。
转载于《图像信号处理器ISP的实现和FPGA验证》 浙江大学 薛江
这篇关于一种基于bayer型模式的双边自适应滤波器的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






