本文主要是介绍多元高斯分布是非参_广义高斯分布(GGD)和非对称广义高斯分布(AGGD),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《No-Reference Image Quality Assessment in the Spatial Domain》,BRISQUE。
1. 广义高斯分布,generalized Gaussian distribution,GGD
1.1 描述
零均值的广义高斯分布如下:
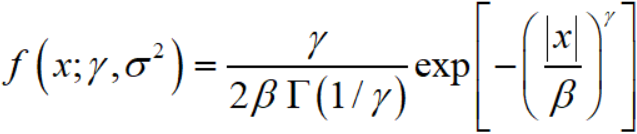
其中
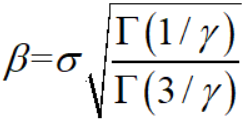
而 Γ(·) 是gamma函数。
形状参数 γ 控制分布的“形状”,而 σ² 控制方差。
例如另 γ = 2 就会得到零均值的高斯分布:
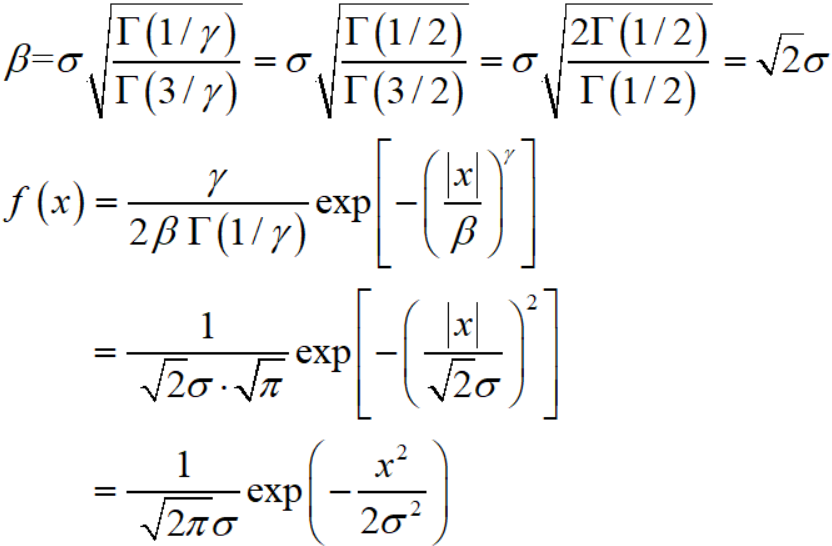
首先记
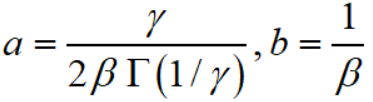
这篇关于多元高斯分布是非参_广义高斯分布(GGD)和非对称广义高斯分布(AGGD)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








