《视觉slam十四讲》第三讲 visualizeGeometry代码讲解——基于vscode软件

      在看完高博的《视觉slam十四讲》中的第三讲——三维空间刚体运动的理论知识后，跑了一下他所提供的相应的代码，在ch3中，稍微有些难度的是visualizeGeometry这一部分代码，同时网上对于这一部分的介绍要么比较分散，要么不是很全面，不是很透彻，于是乎在这篇文章中，我将详细介绍该部分代码,以此也来作为我的学习笔记。鉴于本人实力有限，有些地方介绍的可能不是很恰当，还请各位读者谅解。

    由于之前学了一部分ROS机器人的开发，所基于的平台是vscode软件，所以为了偷懒，在进行slam代码仿真时也将用vscode软件。接下来我将为大家介绍从下载源代码->代码仿真问题解决方法->pangolin库安装->代码解析的保姆级教程。

    1.首先介绍的是高博《视觉slam十四讲》所有源代码的下载：

在linux系统下，打开终端，输入：

git clone https://github.com/gaoxiang12/slambook

 出现如上图所示，表明下载成功。

    2.1下载好代码后，好奇心驱使我赶紧打开代码跑一下，但是在仿真ch3中的visualizeGeometry代码时，先是出现Eigen/Core头文件无法包含，解决方法：

将原来的代码：

#include <Eigen/Core>
#include <Eigen/Geometry>

改成：

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Geometry>

2.2同时又出现出现无法包括Pangolin库函数，解决方法：

（1）.下载功能包

git clone https://github.com/stevenlovegrove/Pangolin.git

（2）.开始编译，打开终端依次输入以下代码：

cd Pangolin
mkdir build
cd build
cmake ..
cmake --build .

（3）.这一步至关重要！！如果不加上后面会报错！！！（就在上面运行完的终端中接着运行）

sudo make install

（4）.然后在安装的文件夹Pangolin下找到build,进入这个文件夹并在这个文件夹打开终端（记住一定要在安装的pangolin的build文件夹下打开终端，否则无法成功），然后

cd Pangolin/build/examples/HelloPangolin

./HelloPangolin

如果出现以下的图片说明安装成功：

（5）随后在vscode运行visualizeGeometry代码时，常规操作像创建功能包，添加依赖这些就不过多的赘叙。这些基操弄好后，在相应的cmake文件中添加以下代码：

find_package(Pangolin REQUIRED)
include_directories(
# include
"/usr/include/eigen3"
${catkin_INCLUDE_DIRS}
${serial_INCLUDE_DIRS}
${eigen_INCLUDE_DIRS}
)
target_link_libraries( "你的文件名"
${Pangolin_LIBRARIES}
${catkin_LIBRARIES}
)

注：以上的代码要放在add_executable(文件名 src/文件名.cpp)这段代码后面。否则会报错。

第一次仿真Pangolin代码时，建议在运行以下代码后，

 source ./devel/setup.bash

再加一句：

sudo ldconfig

    接下来还是有必要提一下Pangolin库，因为在之后的ORB_SLAM中，其显示模块是由pangolin编写的，这个库还是挺重要的。Pangolin是一个基于OpenGL的轻量级开源绘图库，在许多开源SLAM算法（例如ORB-SLAM）中都会用来进行可视化操作。现在我对于pangolin库还是不大了解，有几个网站推荐给大家，对于之后学习Pangolin可能会有帮助：

• 教程代码：https://github.com/yuntianli91/pangolin_tutorial
• ROS Pangolin手册：pangolin namespace

http://docs.ros.org/en/fuerte/api/pangolin_wrapper/html/namespacepangolin.html#a0e2231a25f298cd020cadcd59234f766

3.接下来上代码

#include <iostream>
#include <iomanip>
using namespace std;
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Geometry>
using namespace Eigen;
#include <pangolin/pangolin.h>
//创建选择矩阵结构体
struct RotationMatrix
{Matrix3d matrix = Matrix3d::Identity();//在定义该矩阵变量时，创建一个同尺寸同数据类型的                                                                 //单位阵，对其初始化。     
};
//重载<<符号，对应旋转矩阵
ostream& operator << ( ostream& out, const RotationMatrix& r ) 
{out.setf(ios::fixed);Matrix3d matrix = r.matrix;out<<'=';out<<"["<<setprecision(2)<<matrix(0,0)<<","<<matrix(0,1)<<","<<matrix(0,2)<<"],"<< "["<<matrix(1,0)<<","<<matrix(1,1)<<","<<matrix(1,2)<<"],"<< "["<<matrix(2,0)<<","<<matrix(2,1)<<","<<matrix(2,2)<<"]";return out;
}istream& operator >> (istream& in, RotationMatrix& r )
{return in;
}
//平移量结构体
struct TranslationVector
{Vector3d trans = Vector3d(0,0,0);
};
//重载<<符号，对应平移
ostream& operator << (ostream& out, const TranslationVector& t)
{out<<"=["<<t.trans(0)<<','<<t.trans(1)<<','<<t.trans(2)<<"]";return out;
}istream& operator >> ( istream& in, TranslationVector& t)
{return in;
}
//构建四元数结构体
struct QuaternionDraw//声明了一个QuaternionDraw结构
{Quaterniond q;
};
//重载<<符号，对应四元数 
ostream& operator << (ostream& out, const QuaternionDraw quat )
{auto c = quat.q.coeffs();//auto的原理就是根据后面的值，来自己推测前面的类型是什么。auto的//作用就是为了简化变量初始化，如果这个变量有一个很长很长的初始化类型，就可以用auto代替。out<<"=["<<c[0]<<","<<c[1]<<","<<c[2]<<","<<c[3]<<"]";return out;
}istream& operator >> (istream& in, const QuaternionDraw quat)
{return in;
}int main ( int argc, char** argv )
{//Pangolin是一个基于OpenGL的轻量级开源绘图库pangolin::CreateWindowAndBind ( "visualize geometry", 1000, 600 );//创造一个长宽为1000*600的可视窗口glEnable ( GL_DEPTH_TEST );//初始化OpenGL，创建深度测试，如果不加这个我们看到的就是透明的//创建相机视图pangolin::OpenGlRenderState s_cam (pangolin::ProjectionMatrix ( 1000, 600, 420, 420, 500, 300, 0.1, 1000 ),pangolin::ModelViewLookAt ( 3,3,3,0,0,0,pangolin::AxisY ));const int UI_WIDTH = 500;//创建交互视角pangolin::View& d_cam = pangolin::CreateDisplay().SetBounds(0.0, 1.0, pangolin::Attach::Pix(UI_WIDTH), 1.0, -1000.0f/600.0f).SetHandler(new pangolin::Handler3D(s_cam));// 创建数据表格，操作台pangolin::Var<RotationMatrix> rotation_matrix("ui.R", RotationMatrix());//创建一个矩阵pangolin::Var<TranslationVector> translation_vector("ui.t", TranslationVector());pangolin::Var<TranslationVector> euler_angles("ui.rpy", TranslationVector());pangolin::Var<QuaternionDraw> quaternion("ui.q", QuaternionDraw());pangolin::CreatePanel("ui").SetBounds(0.0, 1.0, 0.0, pangolin::Attach::Pix(UI_WIDTH));while ( !pangolin::ShouldQuit() ){glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );//清屏d_cam.Activate( s_cam );//开启摄像头pangolin::OpenGlMatrix matrix = s_cam.GetModelViewMatrix();//相机模型可视化矩阵赋值给matrix，作为变换矩阵Matrix<float,4,4> m = matrix;// m = m.inverse();RotationMatrix R; //接下来是求反向变换，把相机的坐标系转化为世界坐标系for (int i=0; i<3; i++)for (int j=0; j<3; j++)R.matrix(i,j) = m(j,i);//把4*4矩阵中的3行3列转置后给R.matrixrotation_matrix = R;//取出m中的旋转矩阵TranslationVector t;t.trans = Vector3d(m(0,3), m(1,3), m(2,3));t.trans = -R.matrix*t.trans;translation_vector = t;//取出m中的平移向量TranslationVector euler;euler.trans = R.matrix.transpose().eulerAngles(2,1,0);//transpose是转置euler_angles = euler;//取出欧拉角QuaternionDraw quat;quat.q = Quaterniond(R.matrix);quaternion = quat;//取出四元数glColor3f(1.0,1.0,1.0);pangolin::glDrawColouredCube();//画立方体// 画原始坐标轴glLineWidth(3);glColor3f ( 0.8f,0.f,0.f );glBegin ( GL_LINES );glVertex3f( 0,0,0 );glVertex3f( 10,0,0 );glColor3f( 0.f,0.8f,0.f);glVertex3f( 0,0,0 );glVertex3f( 0,10,0 );glColor3f( 0.2f,0.2f,1.f);glVertex3f( 0,0,0 );glVertex3f( 0,0,10 );glEnd();pangolin::FinishFrame();}
}

    然后再详细介绍其中我感觉比较难懂的函数和代码部分：

3.1考虑到像旋转矩阵、平移、欧拉角、四元数等不能通过简单的cout输出，像旋转矩阵的输出是个矩阵，平移量为向量，四元数输出是个数，因此需要进行各自的输出重载，于是乎在代码中对“<<”进行重载。语法格式如下：

1. <返回类型> operator <运算符符号>（<参数>）

2. {

3. <定义>;

4. }

3.2 相机的坐标系和世界坐标系间可通过欧式变化进行转化，表达式如下;

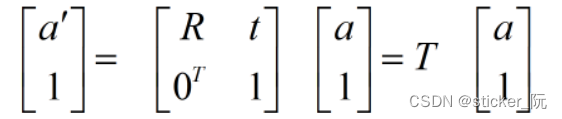
其中，T为变换矩阵，等式左边的向量为相机坐标系的坐标，即

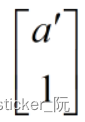
 等式右边为世界坐标系的坐标，即

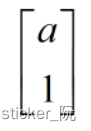
 而在代码中，我们需要得到的是世界坐标系下的坐标，因此需要对变换矩阵T进行求逆运算，表示一个反向的变换，变换后矩阵为：

 这样的话，代码中涉及到的求解反变换下的旋转矩阵，平移量，欧拉角，四元数就好理解了。