问题 B: 手套(原题：无限手套) (dp+两重前缀优化/生成函数)

https://ac.nowcoder.com/acm/contest/186/D

思路：

比赛的时候第一眼生成函数不会。赛后学弟说可以dp

设dp[i][j]表示前i个，选了j个宝石的代价和。考虑对当前取k个，可以得出一个暴力的dp。

先放上学弟的暴力dp理理

#include<bits/stdc++.h>
using namespace std;
long long i,j,m,n,s,t,x,y,z,k;
long long a[1010][10010],b[10010];
int main()
{int ch=998244353;scanf("%lld",&n);for (i=0;i<=10000;i++){b[i]=i*i%998244353;}for (i=1;i<=1000;i++){a[0][i]=0;a[i][0]=1;}scanf("%lld%lld",&x,&y);for (i=1;i<=10000;i++)a[1][i]=(x*b[i]%998244353+y*i%ch+1)%998244353;for (i=2;i<=n;i++){scanf("%lld%lld",&x,&y);for (j=1;j<=10000;j++){for (k=0;k<=j;k++)a[i][j]=(a[i][j]+a[i-1][k]*(x*b[j-k]%ch+y*(j-k)%ch+1))%ch;}}scanf("%lld",&s);for (i=1;i<=s;i++){scanf("%lld",&m);printf("%lld\n",a[n][m]);}
}

然后我们发现这个dp还是可以优化的。我自己推的常数比较大，跑了700ms。网上的推的还有bw大佬推的跑了200ms。

然后我推出来和别人不一样，讨论了快一天。就是说这个题其实最后推的式子对就好了。其形式会有很多不一样的。

比如zzy学弟推的是这样的

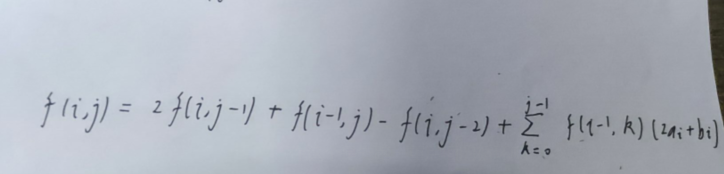
那我自然是人傻常数大阿

附上推导

因为内存超限要压缩一维前缀和

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<cstdio>
#include<algorithm>
#define debug(a) cout<<#a<<"="<<a<<endl;
using namespace std;
const int maxn=1e3+100;
typedef long long LL;
const LL mod=998244353;
inline LL read(){LL x=0,f=1;char ch=getchar();	while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;}
LL dp[maxn][10010];
LL h[10010];
LL g[10010];
LL a[maxn],b[maxn];
int main(void){LL m;m=read();for(int i=1;i<=m;i++) a[i]=read(),b[i]=read();dp[0][0]=1;for(LL i=1;i<=m;i++){for(LL j=0;j<=1e4;j++) h[j]=g[j]=0;for(LL j=0;j<=1e4;j++){///dp[i][j]=(dp[i][j-1]%mod+dp[i-1][j]%mod+(dp[i-1][j-1]%mod*(a[i]+b[i])%mod)%mod+h[i][j-1]%mod+g[i][j-1]%mod+2*a[i]*dp[i-1][j-2]%mod)%mod;dp[i][j]=(dp[i][j]+dp[i-1][j])%mod;if(j>=1) dp[i][j]=(dp[i][j]%mod+dp[i][j-1]%mod+dp[i-1][j-1]%mod*(a[i]+b[i]))%mod;if(j>=1) dp[i][j]=(dp[i][j]%mod+h[j-1]%mod+g[j-1]%mod)%mod;if(j>=2) dp[i][j]=(dp[i][j]%mod+2*a[i]*dp[i-1][j-2]%mod)%mod;h[j]=(dp[i][j]-dp[i-1][j]);if(j>=1) h[j]=(h[j]-dp[i][j-1]);while(h[j]<0) h[j]=(h[j]+mod);h[j]%=mod;if(j>=1)  g[j]=(g[j]+g[j-1])%mod;if(j>=2)  g[j]=(g[j]+2*a[i]*dp[i-1][j-2]%mod)%mod;///g[i][j]=(g[i][j-1]%mod+2*a[i]*dp[i-1][j-2]%mod)%mod;}}LL q;q=read();while(q--){LL n;n=read();printf("%lld\n",dp[m][n]);}return 0;
}

另附zbw和zzy的代码

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<cstdio>
#include<algorithm>
#define debug(a) cout<<#a<<"="<<a<<endl;
using namespace std;
const int maxn=1e3+100;
typedef long long LL;
const LL mod=998244353;
inline LL read(){LL x=0,f=1;char ch=getchar();  while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;}
LL dp[maxn][10010];
LL a[maxn],b[maxn];
int main(void){cin.tie(0);std::ios::sync_with_stdio(false);LL m;cin>>m;for(LL i=1;i<=m;i++){cin>>a[i]>>b[i];}dp[0][0]=1;for(LL i=1;i<=m;i++){LL tp1=0;LL tp2=0;for(LL j=0;j<=1e4;j++){dp[i][j]=(dp[i][j-1]%mod+dp[i-1][j]%mod+tp2)%mod;tp2=(tp2+tp1)%mod;tp2=(tp2+(a[i]+b[i])*dp[i-1][j]%mod)%mod;tp1=(tp1+2*dp[i-1][j]*a[i]%mod)%mod;}}LL q;cin>>q;while(q--){LL n;cin>>n;cout<<dp[m][n]<<"\n";}return 0;
}

#include<bits/stdc++.h>
using namespace std;
long long i,j,m,n,s,t,x,y,z,k;
long long a[1010][10010],b[10010];
int main()
{int ch=998244353;scanf("%lld",&n);for (i=0;i<=10000;i++){b[i]=i*i%998244353;}for (i=1;i<=1000;i++){a[0][i]=0;a[i][0]=1;}scanf("%lld%lld",&x,&y);for (i=1;i<=10000;i++)a[1][i]=(x*b[i]%998244353+y*i%ch+1)%998244353;for (i=2;i<=n;i++){scanf("%lld%lld",&x,&y);for (j=1;j<=3;j++){for (k=0;k<=j;k++)a[i][j]=(a[i][j]+a[i-1][k]*(x*b[j-k]%ch+y*(j-k)%ch+1))%ch;}for (j=4;j<=10000;j++){a[i][j]=(a[i-1][j]+(x+y-2)*a[i-1][j-1]%ch+(x-y+1)*a[i-1][j-2]%ch+a[i][j-1]+2*(a[i][j-1]-a[i][j-2])-(a[i][j-2]-a[i][j-3]))%ch;while (a[i][j]<0)a[i][j]=a[i][j]+ch;}}scanf("%lld",&s);for (i=1;i<=s;i++){scanf("%lld",&m);printf("%lld\n",a[n][m]);}
}

心态爆炸的5.10号