微积分引子

微积分

只是想写一写加深印象而已，作者是个蒟蒻。（借鉴了很多其他题解的解释）

看了一些大佬们关于微积分的讲解，逐步摸清了微积分的轮廓。
对于微积分最关键也是源头来源于不规则几何形状的求解。

譬如举个例子：

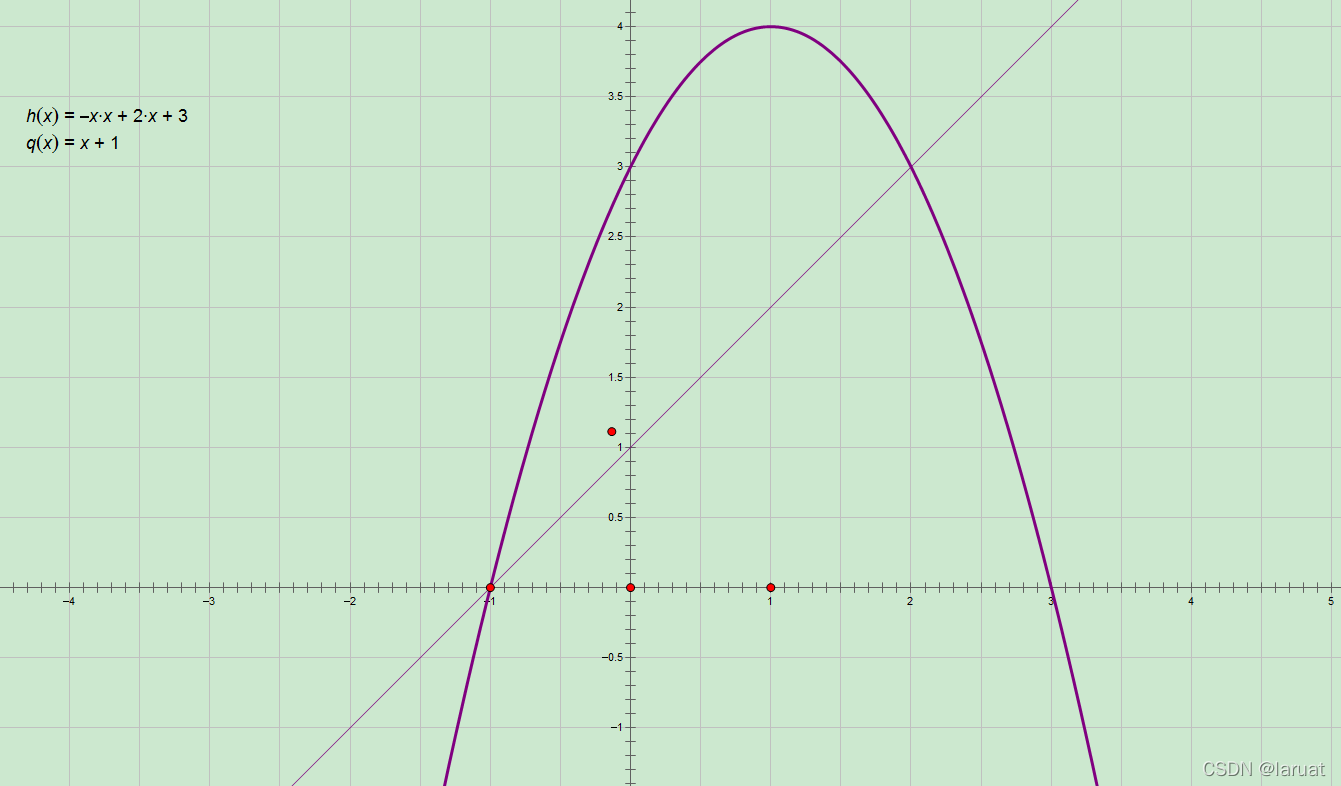
这个一次函数和二次函数之间围成的矩形怎么求解？（思考一下）

在这里我们就需要用到极限思想去想方设法去用规则的图形逼近这个不规则的曲面的面积，我们可以用三角形。

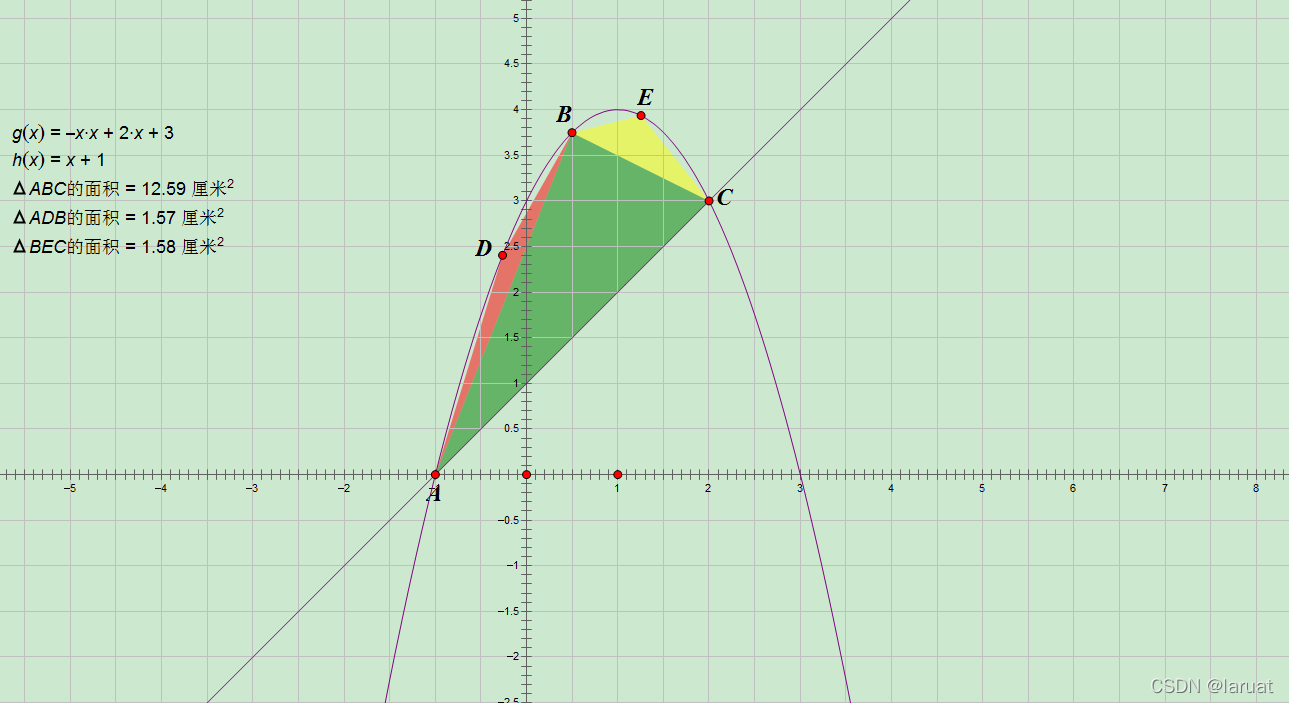
请注意并不是可以将三角形随便乱摆，我们要尽可能要用三角形覆盖掉尽可能多的面积，也就是初中所学的关于此类问题三角形的最大值，其实作者做的这个图不太完美，大家可以仔细观察可以得到，中间的三角形的面积等于左右两旁三角形面积和的4倍（误差是由精度造成的）。然后就像这样再以各两旁三角形为基础往各自两个曲面尽可能的放进一个三角形。

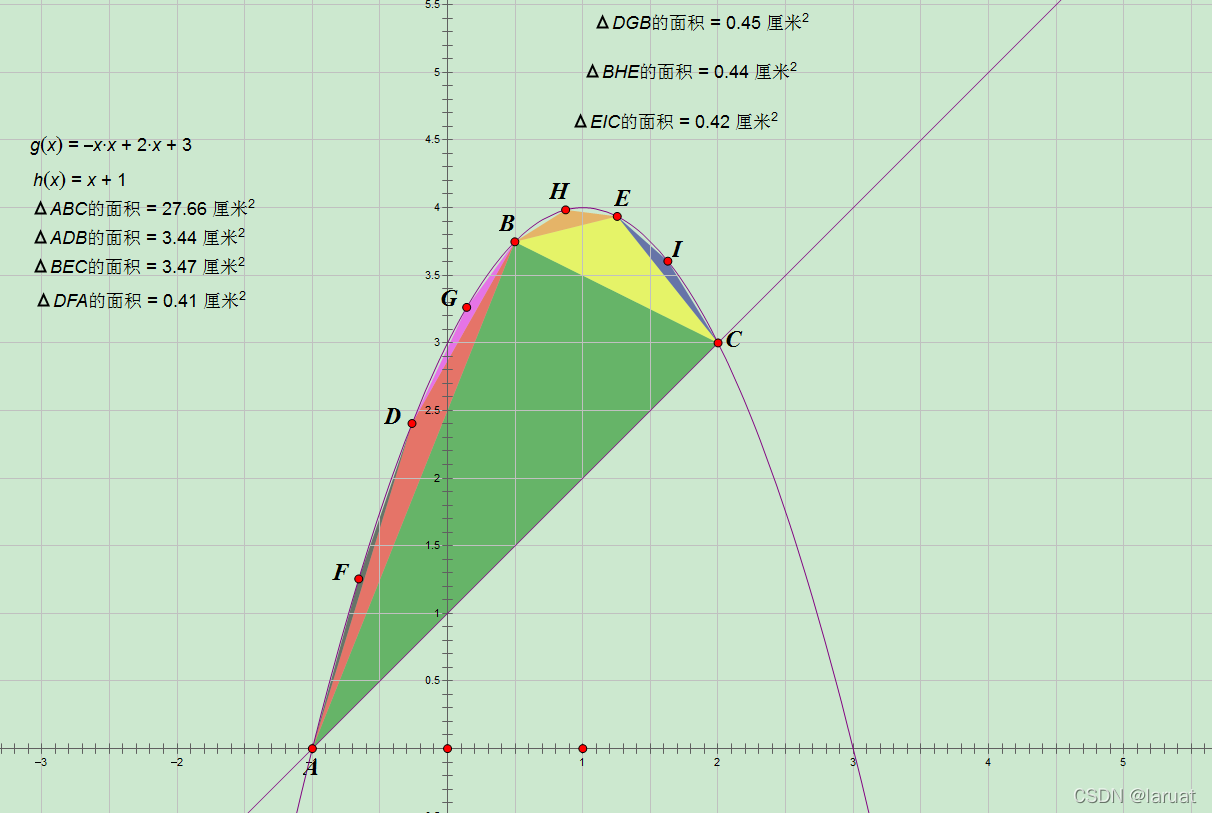
可以发现这新加入的四个三角形又是前两个三角形的面积和的1/4倍。

那么我们可以一直放三角形一直放到无限接近于此曲面的面积。假设我放了n轮三角形，（已经无限接近曲面面积）。三角形ABC面积为x。
则有

$Sn=x+\frac{1}{4}x+(\frac{1}{4}{)}^{2}x+...+(\frac{1}{4}{)}^n$

很明显这是一个等比数列求和，套进去。

等比数列：

$Su{m}_n=\frac{a1(1-q^n)}{1-q}x$

$Sn=\frac{4-\frac{1}{4^{n-1}}}{3}x$

当n趋向于无穷多时，可以把$-\frac{1}{4^{n-1}}$视为零，也就是说这个曲面的面积为$\frac{4}{3}x$。

这里就是具有类似于积分的思想了，那么我们接着拓展。

对于曲面面积的计算其实大部分时候用的是矩形来逼近。

就例如$f(x)=x^2$

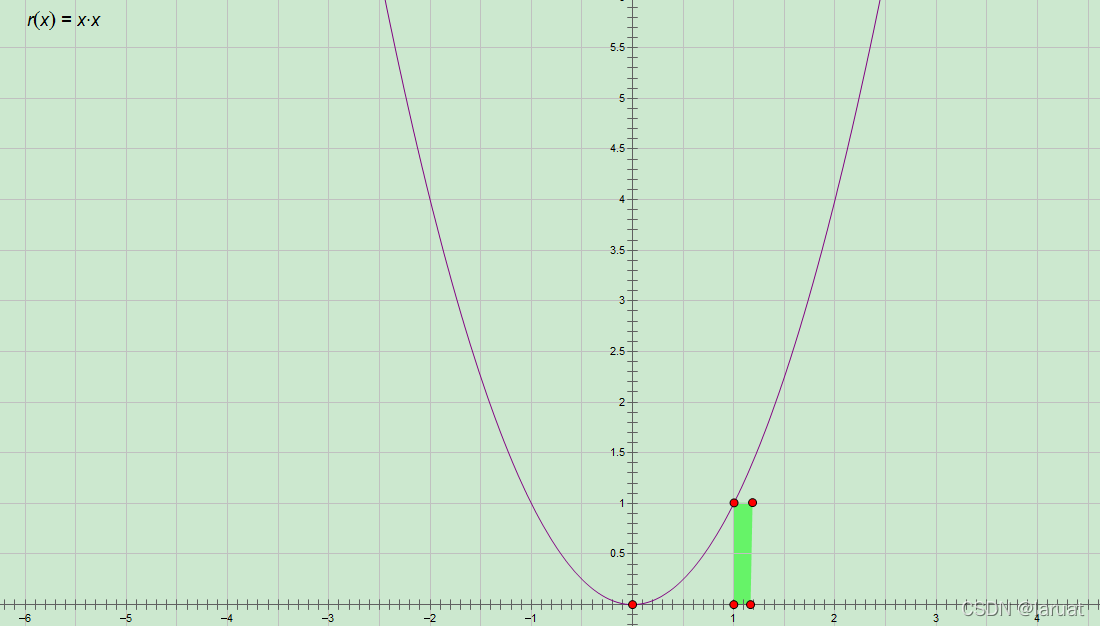
看到那个绿色的矩形了吗，（画的粗糙了），我们把它的横长缩小到无限小，从我们的视角来看，这个矩阵是不是就很贴近这个二次函数了。（脑补一下）

那么我们来求一下这个函数0~1部分与x轴之间的面积，又是一个曲面，但这次大家可以尝试着自己写一下面积表达式。(0 ~ 1之间分成x个矩阵)

$$Sn=\frac{1}{x}(\frac{1}{x}{)}^2+\frac{1}{x}(\frac{2}{x}{)}^2+...+\frac{1}{x}(\frac{x}{x}{)}^2$$

因式分解：

$$Sn=\frac{1}{x^3}(1^2+2^2+...+x^2)$$

然后就用平方和公式化简一下。

$$Sn=\frac{1}{x^3}(\frac{2x^3+3x^2+x}{6})$$

$$Sn=\frac{1}{3}+\frac{1}{2x}+\frac{1}{6x^2}$$

很明显，跟上面的例子一样，x趋近于无限大时，后面两项都可以省略，曲面面积就为1/3。

其实这两个的过程实际上是微积分中积分的部分。

对于第二个例子我们可以通过一个式子来表示

$${\int }_0^{1}f(x)dx$$

表示的就是在0~1范围里f(x)与x轴围成的面积，其中f(x)*dx表示的其实就是一个个矩形的面积，dx表示无限小的横长。

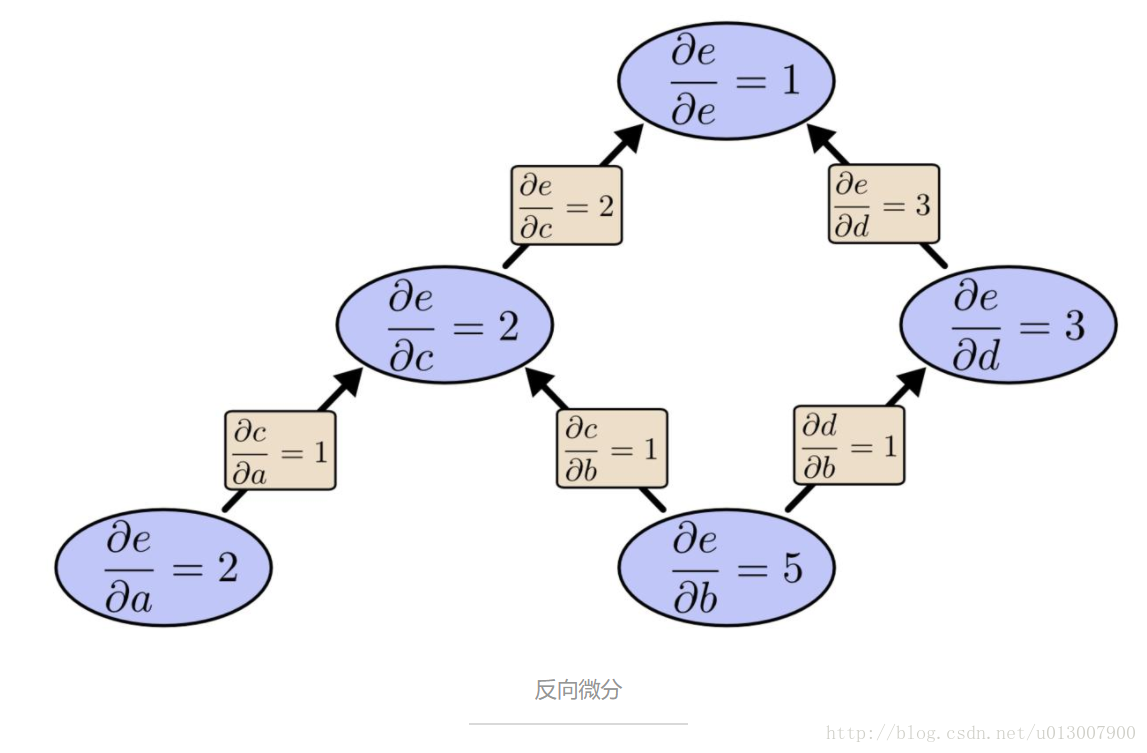
其实微积分的精髓就是微分和积分的相互转换，他们其实是一对互逆运算的关系。也就是说反向积分为微分，反向微分为积分。

然后我们再说说关于微分的部分，关于这一部分，就不得不涉及到求导的应用了。
对于f(x)有导函数f‘(x)。（导函数简单来说其实就是原函数个点的斜率函数）

举个例子。f(x)=$\frac{1}{3}{x}^3$

那么它的导函数就应该为$f^{\prime }(x)=\frac{f(x+dx)-f(x)}{dx+x-x}$

算出来$f^{\prime }(x)=x^2$

那我们再把上面的问题掏出来问一遍，$f(x)=x^2$ 0~1的函数图像与x轴围成的面积为多少。

很简单，直接就是原函数$f(1)-f(0)=\frac{1}{3}$

这就算完了。这就是微积分就重要的思想体现之一，对于一个函数，反向求导可以b表示其函数的面积，你想一想是不是。

于是就有了微积分基本定理，也称牛顿-莱布尼茨公式，令F(x)为f(x)的反向求导的结果（反向微分）,也就是它的原函数。

那么就有

$${\int }_a^{b}f(x)dx=F(b)-F(a)$$

还有就是关于极小值的问题（因为这个数十分不严谨），这一个会有一个$\epsilon -\delta$极限来定义。

这就是求导成为了这个样子。

$$f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{x+\Delta x-x}$$

这里严格用极限这个定义来解释了无限趋近这一动态问题。使微积分开始变为了一个严谨的数学概念。