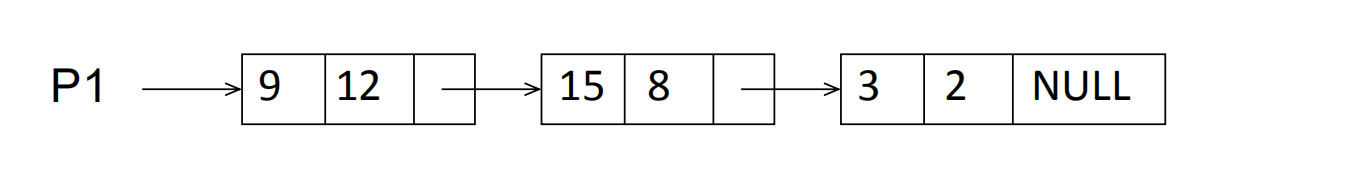引子专题
【小程序开发】答案之书——引子
《答案之书》小程序开发之旅 项目灵感&概述 在生活中,我们时常会面临各种选择和困惑:今天的工作会顺利吗?这次旅行会给我带来惊喜吗? 《答案之书》便是在这样一种灵感下诞生的。 它是一款带有神秘色彩的小程序,旨在通过简单的互动,给予用户一些启发和引导,让他们在疑惑中找到一些微妙的方向感。 通过这个小程序,用户可以带着自己心中的疑问,然后通过宇宙的神秘力量(即我们的随机算法)会为他们送上一句或
【引子】C++从介绍到HelloWorld
C++从介绍到HelloWorld 一、C++的介绍1. 简介2. 应用场景3. C++的标准4. C++的运行过程 二、Visual Studio的安装1. 什么是Visual Studio2. Visual Studio
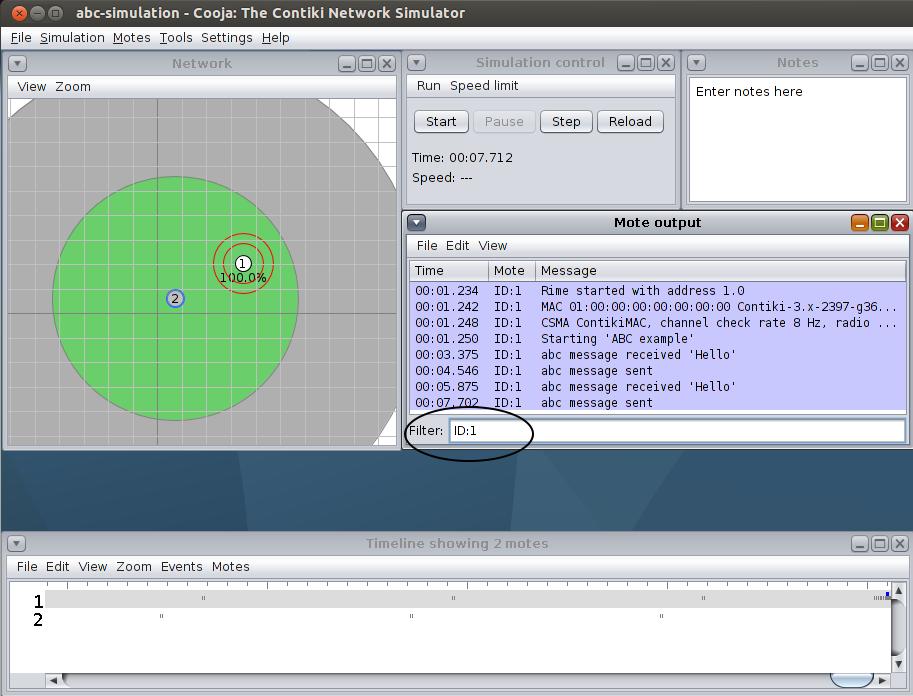
Contiki协议栈Rime:引子introduction
更多的Contiki协议栈知识,请参考索引目录: 《Contiki协议栈:索引目录》 1. 前言 思来想去,既然是程序员,当然还是用一个程序引入比较好。当然,这个程序必须满足以下几点: 足够简单,不会把大家给吓着了能够引入足够多的知识点,可以串起来能够说明包如何在网络中传输 然后我就找啊找,找到了Contiki的一个demo例程:examples/rime/example-abc
QT传输函数控件设计1 引子
这又是一个系列的开头。 说实话本来我想先写写关于QT三维物体显示的功能的,因为后面也会遇到。但是鉴于有些朋友表示急需使用关于渲染的传输函数控件,这里我就先把这个传输函数控件搞定,然后再来写一下怎么实现小三维模型显示和交互。 老规矩:各位务必放心,本人开坑必填,预计一周内填完此坑。 各位注意了,我之前写的关于xml文件读写,以及QT图形图像显示的系列内容都是为这个来做铺垫。以前讲过的这两个系列
FreeRTOS学习第8篇--同步和互斥操作引子
目录 FreeRTOS学习第8篇--同步和互斥操作引子同步和互斥概念实现同步和互斥的机制PrintTask_Task任务相关代码片段CalcTask_Task任务相关代码片段实验现象本文中使用的测试工程 FreeRTOS学习第8篇–同步和互斥操作引子 本文目标:学习与使用FreeRTOS中的同步和互斥操作引子 按照本文的描述,应该可以跑通实验并举一反三。 本文实验条件:拥有
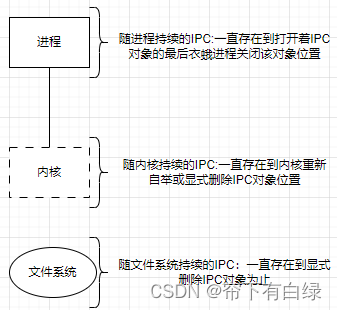
Unix进程间通信之简介-总体概述和引子
目录标题 0. 前言1. 概述2. 进程、线程与信息共享3. IPC对象的持续性4. 名字空间5. fork、exec和exit对IPC对象的影响6. 出错处理: 包裹函数7. Unix标准8. 小结 0. 前言 进程间通信这块是学习linux-c编程的关键, 这篇为后续进程间通信技术的引子篇,后续讲到单独的某一个系统调用 都附该引用。 1. 概述 IPC是进程间通信
支持向量机入门系列-1:引子
好了,现在开始写支持向量机系列,希望能坚持下去。 仅供参考,请勿转载,因为随时都可能会修改。 第一部分 引子 1. 支持向量机的目的是什么? 对于用于分类的支持向量机来说,给定一个包含正例和反例(正样本点和负样本点)的样本集合,支持向量机的目的是寻找一个超平面来对样本进行分割,把样本中的正例和反例用超平面分开,但是不是简单地分看,其原则是使正例和反例之间的间隔最大。
【浙大数据结构学习笔记】2.1.1 引子——多项式的表示
2.1.1 引子——多项式的表示 多项式: f ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n − 1 x n − 1 + a n x n f(x)=a_{0}+a_{1}x+a_{2}x^{2}+\cdots+a_{n-1}x^{n-1}+a_{n}x^{n} f(x)=a0+a1x+a2x2+⋯+an−1xn−1+anxn 表示多项式的关键数据:
带你学会C++文字页面类项目——2.引子与首页部分制作
目录 🔮前言 ⭐声明部分 🌌引子部分制作 🔋首页部分制作 🧳总结 🔮前言 往期链接:1.初步引入与知识储备 上一期我带大家认识了C++文字页面类项目和基础知识,这一次,我们来学习运用它们来进行运用。 ⭐声明部分 之前讲到,在做任何比较大且函数量多的项目,需要运用先声明再定义的函数定义方式,以便结构清晰,
深度学习——引子note
文章目录 深度学习应用特点框架比较TensorFlow 基本深度学习概念 深度学习 深度学习传统到现在的推动因素: 理论:CNN,RNN,ReLU(非线性激励函数) 数据:ImageNet,LFW 硬件:Nvidia CUDA+GPU 应用特点 优点: 学习能力强 覆盖范围广,适应性好 可移植性好 缺点: 计算量大,便携性差 硬件需求高 模型设计复杂 有可能被"hack"
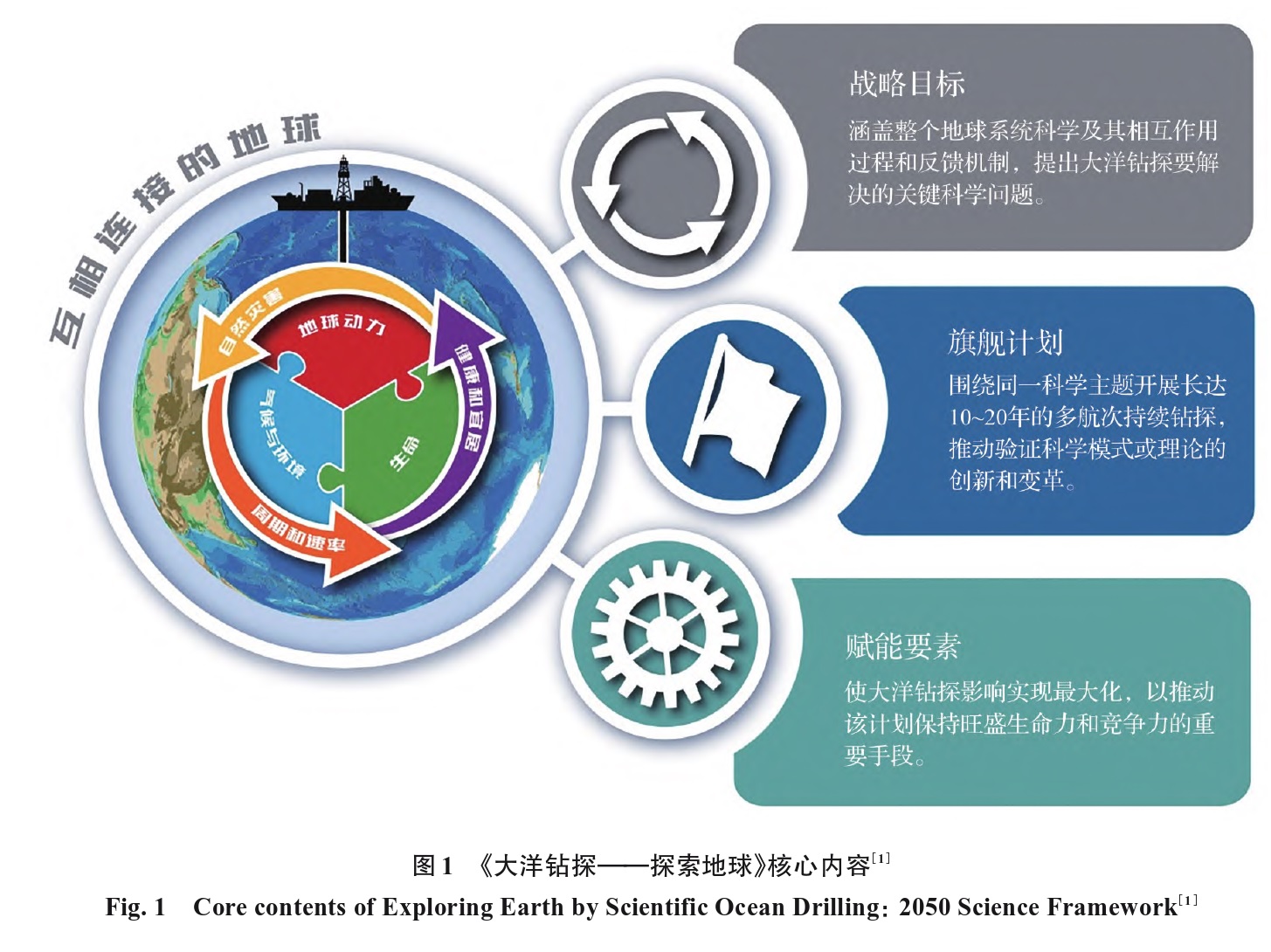
大洋钻探系列之一引子
大洋科学钻探计划自1968年启动开始,迄今已有50余年,先后经历了4个阶段。深海钻探计划(Deep Sea Drilling Program,DSDP,1968-1983年)、国际大洋钻探计划(Ocean Drilling Program,ODP,1985-2003年)、综合大洋钻探计划(Integrated Ocean Drilling Program,IODP,2003-2013年)和正在进行
1、搭建一个后台服务器--引子
最近去了几家公司面试,有一些大公司(比如企鹅)的考核内容真心弱智,考的都是些算法,尼玛,拿一个刚毕业的学生来做说不定也可以过的,看来本来就不是在招搞服务器的,举个例子,企鹅多个部门都曾出的一道题:如何知道集合A,B中的相关性。 意思就是哪些元素在A,B之中都有,哪些元素在A,B中不都出现。 其实解法很简单,学过算法的完全可以做到 。我们知道集合具有互异性,就是集合中的元素只能出现一次,可以建一