2663 Tri Tiling 完美覆盖，样例分析+详细题解-只需10行代码

描述

一张普通的国际象棋棋盘，它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌，每张牌恰好覆盖棋盘上相邻的两个方格，即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么，是否能够把 32 张多米诺牌摆放到棋盘上，使得任何两张多米诺牌均不重叠，每张多米诺牌覆盖两个方格，并且棋盘上所有的方格都被覆盖住？我们把这样一种排列称为棋盘被多米诺牌完美覆盖。这是一个简单的排列问题，同学们能够很快构造出许多不同的完美覆盖。但是，计算不同的完美覆盖的总数就不是一件容易的事情了。不过，同学们 发挥自己的聪明才智，还是有可能做到的。
现在我们通过计算机编程对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。

任务
对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。

输入

一次输入可能包含多行，每一行分别给出不同的 n 值 ( 即 3 乘 n 棋盘的列数 )。当输入 -1 的时候结束。

n 的值最大不超过 30.

输出

针对每一行的 n 值，输出 3 乘 n 棋盘的不同的完美覆盖的总数。

思路

看着有点麻烦，其实不难，代码10行就够了。
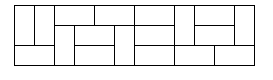
首先对$n=2$时，对3*2的棋盘我们有三种（丑，勿怪）覆盖方式

对样例来说有12行，我们挑几种形式来分析一下

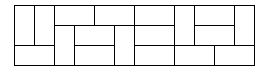
• $n$是奇数，可以考虑一列，三列，5列的情形，你会发现，只要是奇数列，我们完全没有办法把他填充完整，因此我们可以考虑以两列为一个单位。
• 记函数$f(n)$为在$n$列时的覆盖方案数目，$f(0)=1$，为什么这么初始化？看$f(2)$我们以两列为一个单位，那么他必定与$f(0)$的排列总数有关，而$f(2)=3$是0号位置的排列数目之和*[1-2]位置的排列方法数目，因此初始化为1.
• 再来看看$f(4)$，也就是下图红线框起来的部分。首先考虑他最右边两列有三种情况，承上之前的排列数即$f(2)\ast 3$，不止如此，他的四列也可能长蓝线框起来这样，这种情况下有几种组合呢，答案是$f(0)\ast 2$。
  
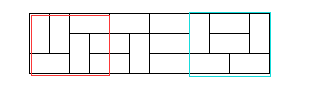
• 最后我们看看$f(n)$，首先他的最后两列有三种情况$f(n)=3\ast f(n-2)+...$，然后他的最后四列单独拿出来有两种情况$f(n)=3\ast f(n-2)+2\ast f(n-4)+...$，他的最后六列单独拿出来也只有两种情况：于是$f(n)=3\ast f(n-2)+2\ast f(n-4)+2\ast f(n-6)+...$，不断的向前递归我们得到
  
  $$f(n)=3\ast f(n-2)+2\ast f(n-4)+2\ast f(n-6)+...+2\ast f(0)$$
  $$f(n-2)=3\ast f(n-4)+2\ast f(n-6)+...+2\ast f(0))$$
  $$f(n)=4f(n-2)-f(n-4)$$

#include<iostream>
using namespace std;
int f[35];
int main() {int n = 0; f[0] = 1, f[2] = 3;for (int i = 4; i < 35; i++)f[i] = 4 * f[i - 2] - f[i - 4];while (cin >> n && n != -1) {cout << f[n] << endl;}
}