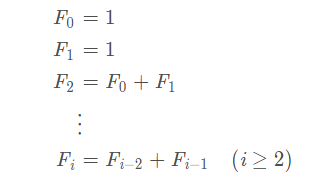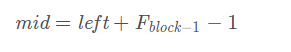斐波那契查找（黄金分割查找算法）

斐波那契

一、摘要

如果从文件中读取的数据记录的关键字是有序排列的（递增的或是递减的），则可以用一种比折半查找法更有效率的查找方法来查找文件中的记录，即为斐波那契查找，也称为黄金分割查找法。

二、什么是斐波那契查找

斐波那契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、····，在数学上，斐波那契被递归方法如下定义：F(1)=1，F(2)=1，F(n)=f(n-1)+F(n-2) （n>=2）。该数列越往后相邻的两个数的比值越趋向于黄金比例值（0.618)。

三、 基本思想

斐波那契查找法与折半查找的基本思想类似，都是减少查找序列的长度，分而治之地进行关键字的查找。他的查找过程是：先确定待查找记录的所在的范围，然后逐渐缩小查找的范围，直至找到该记录为止（也可能查找失败）。
斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数F[n]，将原查找表扩展为长度为Fn，完成后进行斐波那契分割，即F[n]个元素分割为前半部分F[n-1]个元素，后半部分F[n-2]个元素，找出要查找的元素在那一部分并递归，直到找到。
斐波那契查找的时间复杂度还是O(log 2 n )，但是 与折半查找相比，斐波那契查找的优点是它只涉及加法和减法运算，而不用除法，而除法比加减法要占用更多的时间，因此，斐波那契查找的运行时间理论上比折半查找小，但是还是得视具体情况而定。

四、举例

对于斐波那契数列：1、1、2、3、5、8、13、21、34、55、89……（也可以从0开始），前后两个数字的比值随着数列的增加，越来越接近黄金比值0.618。比如这里的89，把它想象成整个有序表的元素个数，而89是由前面的两个斐波那契数34和55相加之后的和，也就是说把元素个数为89的有序表分成由前55个数据元素组成的前半段和由后34个数据元素组成的后半段，那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618，假如要查找的元素在前半段，那么继续按照斐波那契数列来看，55 = 34 + 21，所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段，继续查找，如此反复，直到查找成功或失败，这样就把斐波那契数列应用到查找算法中了。

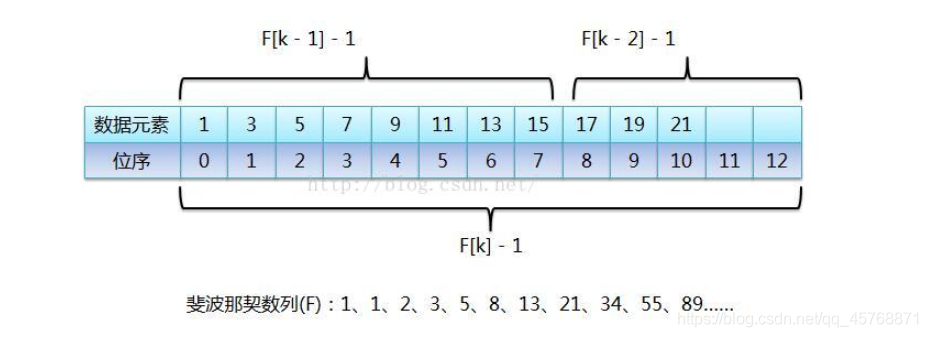
从图中可以看出，当有序表的元素个数不是斐波那契数列中的某个数字时，需要把有序表的元素个数长度补齐，让它成为斐波那契数列中的一个数值，当然把原有序表截断肯定是不可能的，不然还怎么查找。然后图中标识每次取斐波那契数列中的某个值时(F[k])，都会进行-1操作，这是因为有序表数组位序从0开始的，纯粹是为了迎合位序从0开始。

五、如何计算

作为折半查找法的加强优化版，它很好地将黄金分割的思想融入到关键字的查找中，它是根据斐波那契序列的特点对有序表进行分割的。

1、斐波那契数组

斐波那契查找，是二分查找的一个变种。其时间复杂度 O(log2n) 。
斐波那契数列，又称黄金分割数列， F{1,1,2,3,5,8,13,21,34,…}F={1,1,2,3,5,8,13,21,34,…} 数学表达式：

之所以它又称为黄金分割数列，是因为它的前一项与后一项的比值随着数字数量的增多逐渐逼近黄金分割比值0.618。

2、利用斐波那契数组确定元素的位置

所以斐波那契查找改变了二分查找中原有的中值 mid 的求解方式，其 mid 不再代表中值，而是代表了黄金分割点：

二分查找，以一半元素来分割数组；
斐波那契查找，以黄金分割点来分割数组。
假设表中有 n 个元素，查找过程为取区间中间元素的下标 mid ，对 mid 的关键字与给定值的关键字比较：
（1）如果与给定关键字相同，则查找成功，返回在表中的位置；
（2）如果给定关键字大，向右查找并减小2个斐波那契区间；
(3）如果给定关键字小，向左查找并减小1个斐波那契区间；
（4）重复过程，直到找到关键字（成功）或区间为空集（失败）。

它要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1;
开始将k值与第F(k-1)位置的记录进行比较(即mid=low+F(k-1)-1),比较结果也分为三种
(1)key = k[mid], mid位置的元素即为所求;
(2)key>k[mid]，low=mid+1,k-=2;
说明：low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个，所以可以递归的应用斐波那契查找。
(3)key<k[mid],high=mid-1,k-=1。
说明：low=mid+1说明待查找的元素在[low,mid-1]范围内，k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个，所以可以递归 的应用斐波那契查找。

斐波那契搜索也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样的，斐波那契查找也属于一种有序查找算法。

3、举例

举例，假设有集合 e0=2, e1=3, e2=7, e3=14, e4=22, e5=33, e6=55, e7=75, e8=89, e9=123 。
查找元素44的过程：
已知：
元素数量size = 10；
下标区间 [low, high] 为left = 0、right = 9。
则初始化的斐波那契数列为 Fib={1,1,2,3,5,8,13}Fib={1,1,2,3,5,8,13} ，即斐波那契数列最后一位要比size - 1大。
此时查找第一步为：此时刚初始化完，斐波那契数列最后一个区间为第6个区间，即区间(8, 13)；第8个数字为当前黄金分割点，则第8个数字下标为下标7，检测的数字为 e7 ；以8分割数组后，左区间为(1, 8)。

此时查找第二步为：同第一步，黄金分割点为第5个数字下标为4。

上一步结束，还剩 { 33 55 } ，此时查找第三步为：黄金分割点为第2个数字55，它的下标为6。

上一步结束，还剩 { 33 } ，此时查找第四步为：黄金分割点为第1个数字33，它的下标为5。

六、代码实现

1、斐波那契数组实现

//生成斐波那契数列
void  Fibonacci(int* F)
{int i = 0;F[0] = 1;F[1] = 1;for ( i = 2; i < N; ++i){F[i] = F[i - 1] + F[i - 2];}
}

2、斐波那契查找

int search(int* a, int  key, int n)
{int i = 0, low = 0, high = n - 1;int mid = 0, k = 0, F[N];Fibonacci(F);while (n >F[k] - 1)  //计算出N在斐波那契中的数列项{++k;}//当数组不满足时补全数组for ( i = 0; i < F[k]-1; ++i){a[i] = a[high];   //用数组最后一项补全数组}while (low <= high){mid = low + F[k - 1] - 1; //根据斐波那契数列进行分割if (a[mid] > key)   //更小时，在左边{high = mid - 1;k -= 1;   //左边：F[N-1] - 1  总式： F[N] - 1 = F[N-1] - 1 + F[N-2] -1 + 1}else if(a[mid] < key){low = mid + 1; k -= 2;  // 右边：F[N - 12] - 1 }else{if (mid <= high)//如果为真则找到相应位置 return mid;elsereturn -1;}}
}

3、实验数据及测试

#include<stdio.h>
#define N 30//生成斐波那契数列
void  Fibonacci(int* F)
{int i = 0;F[0] = 1;F[1] = 1;for ( i = 2; i < N; ++i){F[i] = F[i - 1] + F[i - 2];}
}
int search(int* a, int  key, int n)
{int i = 0, low = 0, high = n - 1;int mid = 0, k = 0, F[N];Fibonacci(F);while (n >F[k] - 1)  //计算出N在斐波那契中的数列项{++k;}//当数组不满足时补全数组for ( i = 0; i < F[k]-1; ++i){a[i] = a[high];   //用数组最后一项补全数组}while (low <= high){mid = low + F[k - 1] - 1; //根据斐波那契数列进行分割if (a[mid] > key)   //更小时，在左边{high = mid - 1;k -= 1;   //左边：F[N-1] - 1  总式： F[N] - 1 = F[N-1] - 1 + F[N-2] -1 + 1}else if(a[mid] < key){low = mid + 1; k -= 2;  // 右边：F[N - 12] - 1 }else{if (mid <= high)//如果为真则找到相应位置 return mid;elsereturn -1;}}
}
int main()
{int a[N] = { 2,3,5,7,9,11,12,15,19,22 };int k, r = 0;printf("请输入要查找的数字：");scanf_s("%d", &k);r = search(a, k, 10);if (r != -1)printf("\n在数组的第%d个位置找到元素：%d\n", r + 1, k);elseprintf("\n未在数组中找到该元素：%d\n", k);return 0;
}

4、编译环境

Visual Studio 2019

七、后记

折半查找法https://blog.csdn.net/qq_45768871/article/details/104975755
插值查找（比例查找法）https://blog.csdn.net/qq_45768871/article/details/104975698