新疆大学ACM-ICPC程序设计五月月赛-D-勤奋的杨老师-最大权闭合子图

（有任何问题欢迎留言或私聊

题目描述： 传送门

 众所周知，杨老师是一位十分勤奋的老师，他非常的热爱学习。
 勤奋的他为自己罗列了一个学习清单，共有n个知识点，他可以有选择的进行学习。
 每个知识点都会对应0个或1个或多个先修知识点（只有学会了先修知识点才能学习该知识点），同时每个知识点都有一个智慧值和一个智力消耗值。

 杨老师希望在进行过激烈的学习之后，他的收获可以·量化为所有学过的题的智慧值的和与智力消耗值的和的差值。请问，这个值最大是多少？
输入描述:
 第一行：一个整数n（n<=500）接下来n行，每行两个整数，代表第i个知识点的智 慧值和智力消耗值接下来若干行，每行2个整数u, v，代表u是v的先修知识点。
输出描述:
 一行，表示杨老师的收获的最大值

解题思路：

最大权闭合子图：
 1. 要求智慧值和智力消耗值差值的最大，先将所有差值为正的加起来得到sum。
 2. 共n+2个点：源点，汇点，n个知识点。若差值为正，则源点向知识点连边，边权为差值；若为负，则知识点向汇点连边，边权为差值的绝对值。(若为0可连边可不连边)如果u是v的先修知识点，那么v->u连边，边权为INF。
 3. 跑出最小割，代表学n个知识点的最小代价。用sum减去最小割即为答案。

AC代码：

#include<bits/stdc++.h>
#define mm1(a) memset((a),-1,sizeof((a)))  
#define mm0(a) memset((a),0,sizeof((a)))  
#define mmx(a) memset((a),0x3f,sizeof((a)))  
using namespace std;
typedef long long LL;
const int N = 100005;
const int INF = 0x3f3f3f3f;
int n,m,tot,vt,vs;
int d[N],head[N];
struct lp{int to,w,nex;lp(){}lp(int a,int b,int c){to=a;w=b;nex=c;}
}cw[N<<2];
int pigNum[N],pigTo[N];
inline void add(int a,int b,int c){cw[++tot]=lp(b,c,head[a]);head[a]=tot;cw[++tot]=lp(a,0,head[b]);head[b]=tot;
}
bool bfs(){mm1(d);queue<int>Q;Q.push(vt);d[vt]=0;while(!Q.empty()){int u=Q.front();Q.pop();for(int i=head[u];i!=-1;i=cw[i].nex){int v=cw[i].to;if(cw[i^1].w&&d[v]==-1){d[v]=d[u]+1;Q.push(v);}}}return d[vs]!=-1;
}
int dfs(int x,int f){if(x==vt||f==0) return f;int use=0,w;for(int i=head[x];i!=-1;i=cw[i].nex){int to=cw[i].to;if(d[to]==d[x]-1 && cw[i].w){w=dfs(to,min(cw[i].w,f-use));cw[i].w-=w,cw[i^1].w+=w;use+=w;if(use==f) return f;}}return use;
}
inline void init(){tot=-1;mm1(head);mm0(pigTo);vs=0,vt=n+1;
}
int main(){int x,y;scanf("%d",&n);init();int sum=0;for(int i=1;i<=n;++i){scanf("%d%d",&x,&y);if(x-y>=0){sum+=x-y;add(vs,i,x-y);}else {add(i,vt,y-x);}}while(~scanf("%d%d",&x,&y)){add(y,x,INF);}int ans=0;while(bfs())ans+=dfs(vs,INF);printf("%d\n",sum-ans );return 0;
}

本题官方题解：

D 题
求最大权闭合子图。 这里提供一种思路：将每个知识作为点，源点到每个知识建边，边权设为这个知识的智 慧值；将某点的先修知识点与该点建有向边，边权为正无穷；再将每个知识的智力消耗值作 为点，每个知识与他对应的智力消耗值的点建有向边，边权为正无穷；每个智力消耗值的点 与汇点建有向边，边权为智力消耗值；然后用智慧值的和减去该图的最小割即为答案。

证明：
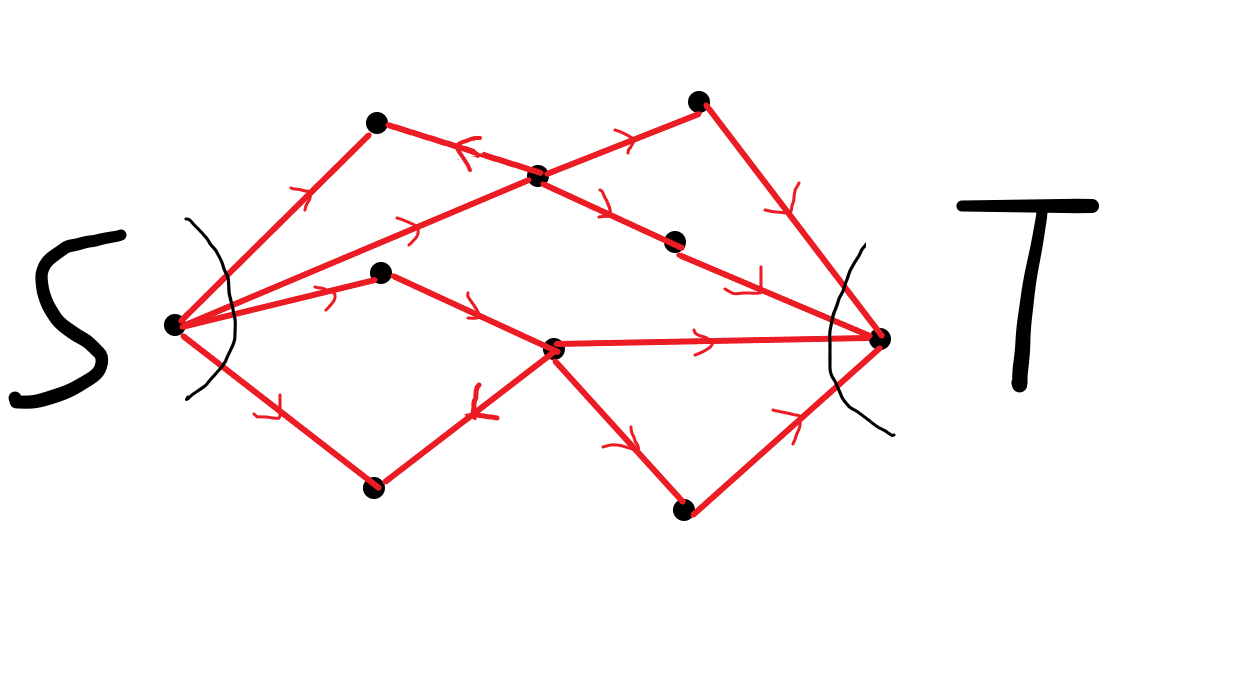
我们知道一个割会把图分成两个部分，一部分是S能走到的，另一部分是能走到T的。 
我们设这两个集合为A，B。A0，B0分别表示A,B中原来点权是负数的点集， A1，B1分别表示A,B中点权原来是正数的点集。由于中间的边是max的，割的一定是和S，T相连的边，这个叫简单割。 
所以割的大小 = |A0| ＋B1 
绝对值表示把负的变成了正的。A，B一定是最大权闭合子图 
A的点权和 = A1 - |A0| 
A的点权和 +　割的大小　＝　A1 + B1 = 全图中的正权点和 
这是一个定值， 要使A的点权和最大， 就要使割最小，就是最小割，至此得证。