本文主要是介绍时间序列预测的Meta N-BEATS方法1,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在时间序列预测中,目前占统治地位的方法仍然是传统的时间序列分析统计方法,虽然有个别方法中融入了深度学习模型,也基本上仅限于利用深度学习来学习这些时间序列统计模型的超参数。Bengio团队最新的Paper,将纯深度学习技术应用于时间序列预测,并在测试数据集上取得了比传统时间充列分析还要好的效果,他们分别发表了两篇文章,第一篇发表于19年5月,讲述了N-BEATS算法,第二篇发表于20年2月,将N-BEATS算法与元学习方法相融合,并且取得了SOTA效果。
本系列博文除了介绍这两篇文章基本概念之外,还会讲解采用PyTorch来复现论文中结果。这两篇文章都是单变量时间序列预列,我们在实际中,使用这种技术,对股市行情(开盘价、最高价、最低价、收盘价、成交量、成交金额等)这种多变量预测模型来进行预测,也取得了效好的应用效果,感兴趣的读者可以多交流。注:基于商业原因,这部分内容没有在本系列博文中出现。
问题描述
我们考虑的是单变量离散时间序列的点预测问题,对于一个时间序列:
v 1 , v 2 , v 3 , . . . , v i , . . . , v T v_{1}, v_{2},v_{3},...,v_{i},..., v_{T} v1,v2,v3,...,vi,...,vT
假设我们要预测H个时间点之后的值。例如,对于我们的股市应用,我们要预测后天的价格涨跌,因此H=2,我们要预测的结果为:
y = [ v T + 1 v T + 2 . . . v T + H ] = [ y 1 y 2 . . . y H ] ∈ R H \boldsymbol{y}=\begin{bmatrix} v_{T+1} \\ v_{T+2} \\ ... \\ v_{T+H} \end{bmatrix} = \begin{bmatrix} y_{1} \\ y_{2} \\ ... \\ y_{H} \end{bmatrix} \in R^{H} y=⎣⎢⎢⎡vT+1vT+2...vT+H⎦⎥⎥⎤=⎣⎢⎢⎡y1y2...yH⎦⎥⎥⎤∈RH
为了预测时间点 t t t后 H H H个时间点的值,我们需要向前看 w ≤ T w \le T w≤T个时间点的值进行预测:
x = [ v T − w + 1 v T − w + 2 . . . v T ] ∈ R w \boldsymbol{x}=\begin{bmatrix} v_{T-w+1} \\ v_{T-w+2} \\ ... \\ v_{T} \end{bmatrix} \in R^{w} x=⎣⎢⎢⎡vT−w+1vT−w+2...vT⎦⎥⎥⎤∈Rw
我们假设网络的预测值为 y ^ \boldsymbol{\hat{y}} y^,我们定义如下误差:
平均绝对值百分比误差(MAPE):
M A P E = 100 H ∑ i = 1 H ∣ v T + i − v ^ T + i ∣ ∣ v T + i ∣ = 100 H ∑ i = 1 H ∣ y i − y ^ i ∣ y i MAPE=\frac{100}{H} \sum^{H}_{i=1} \frac{ \vert v_{T+i} - \hat{v}_{T+i} \vert }{ \vert v_{T+i} \vert } = \frac{100}{H} \sum^{H}_{i=1} \frac{ \vert y_{i} - \hat{y}_{i} \vert}{ y_{i} } MAPE=H100i=1∑H∣vT+i∣∣vT+i−v^T+i∣=H100i=1∑Hyi∣yi−y^i∣
对称平均绝对值百分比误差(sMAPE):
s M A P E = 200 H ∑ i = 1 H ∣ v T + i − v ^ T + i ∣ ∣ v T + i ∣ + ∣ v ^ T + i ∣ = 200 H ∑ i = 1 H ∣ y i − y ^ i ∣ ∣ y i ∣ + ∣ y ^ i ∣ sMAPE = \frac{200}{H} \sum^{H}_{i=1} \frac{ \vert v_{T+i} - \hat{v}_{T+i} \vert }{ \vert v_{T+i} \vert + \vert \hat{v}_{T+i} \vert } = \frac{200}{H} \sum^{H}_{i=1} \frac{ \vert y_{i} - \hat{y}_{i} \vert }{ \vert y_{i} \vert + \vert \hat{y}_{i} \vert } sMAPE=H200i=1∑H∣vT+i∣+∣v^T+i∣∣vT+i−v^T+i∣=H200i=1∑H∣yi∣+∣y^i∣∣yi−y^i∣
平均绝对缩放误差(MASE):
M A S E = 1 H ∑ i = 1 H ∣ v T + i − v ^ T + i ∣ 1 T + H − m ∑ j = m + 1 T + H ∣ v j − v j − m ∣ MASE=\frac{1}{H}\sum^{H}_{i=1} \frac{ \vert v_{T+i} - \hat{v}_{T+i} \vert }{ \frac{1}{T+H-m} \sum^{T+H}_{j=m+1} \vert v_{j} - v_{j-m} \vert } MASE=H1i=1∑HT+H−m1∑j=m+1T+H∣vj−vj−m∣∣vT+i−v^T+i∣
上式中的 m m m为数据的周期。
对于论文中用到的M4数据集,定义总体加权平均(OWA):
O W A = 1 2 [ s M A P E s M A P E n a i v e 2 + M A S E M A S E n a i v e 2 ] OWA=\frac{1}{2}\bigg[ \frac{sMAPE}{sMAPE_{naive2}} + \frac{MASE}{MASE_{naive2}} \bigg] OWA=21[sMAPEnaive2sMAPE+MASEnaive2MASE]
网络组成块
网络最小的组成单位是基本组成块,其结构如下所示:
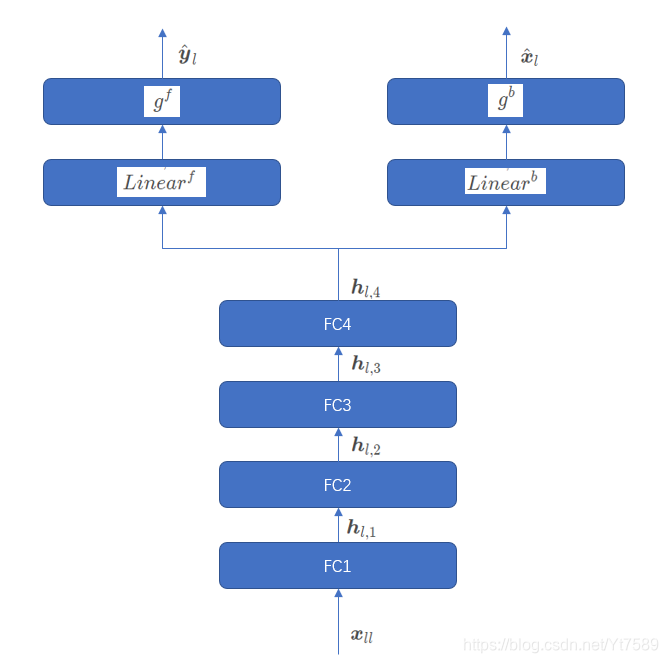
输入信号KaTeX parse error: Expected group after '^' at position 21: …symbol{\hat{x}}^̲_l,其中的 l l l为组成块的索引值,首先进入第一个全连接层 F C 1 FC1 FC1,如下所示:
h l , 1 = R e L U ( W l , 1 x l + b l , 1 ) \boldsymbol{h}_{l,1}=ReLU( W^{l, 1} \boldsymbol{x}_{l} + \boldsymbol{b}^{l,1} ) hl,1=ReLU(Wl,1xl+bl,1)
接着进入第二层 F C 2 FC2 FC2,如下所示:
h l , 2 = R e L U ( W l , 2 h l , 1 + b l , 2 ) \boldsymbol{h}_{l,2}=ReLU( W^{l, 2} \boldsymbol{h}^{l,1} + \boldsymbol{b}^{l,2} ) hl,2=ReLU(Wl,2hl,1+bl,2)
接着进入第三层 F C 3 FC3 FC3,如下所示:
h l , 3 = R e L U ( W l , 3 h l , 2 + b l , 3 ) \boldsymbol{h}_{l,3}=ReLU( W^{l, 3} \boldsymbol{h}^{l,2} + \boldsymbol{b}^{l,3} ) hl,3=ReLU(Wl,3hl,2+bl,3)
接着进入第四层 F C 4 FC4 FC4,如下所示:
h l , 3 = R e L U ( W l , 3 h l , 2 + b l , 3 ) \boldsymbol{h}_{l,3}=ReLU( W^{l, 3} \boldsymbol{h}^{l,2} + \boldsymbol{b}^{l,3} ) hl,3=ReLU(Wl,3hl,2+bl,3)
在第四层之后,输出信号将分为两个分支,分别为前向预测 L i n e a r f Linear^{f} Linearf和后向预测 L i n e a r b Linear^{b} Linearb,我们分别来讨论。
前向预测
首先经过线性变换,如下所示:
θ f , l = W f , l h l , 4 \boldsymbol{ \theta }^{f,l} = W^{f,l} \boldsymbol{h}^{l,4} θf,l=Wf,lhl,4
在这里我们只采用全连接层来实现前向预测,在原始文章中,采用时序信号分析中的趋势和季节因素分析,并且将深度学习与其相结合,可以取得最好的效果,但是对于股市应用而言,趋势可以使用,季节因素就不太适用了,因此我们只采取深度学习方式。
接下来我们预测 T T T时间点到 T + H T+H T+H时间点的预测值:
y ^ l = G f , l θ f , l + g f , l \boldsymbol{\hat{y}}_{l} = G^{f,l} \boldsymbol{\theta}^{f,l} + g^{f,l} y^l=Gf,lθf,l+gf,l
其中 G f , l G^{f,l} Gf,l为连接权值矩阵, g f , l g^{f,l} gf,l为偏置值。
后向预测
首先经过线性变换,如下所示:
θ b , l = W b , l h l , 4 \boldsymbol{ \theta }^{b,l} = W^{b,l} \boldsymbol{h}^{l,4} θb,l=Wb,lhl,4
接着我们进行后向预测,这里我们也仅使用全连接层来实现:
x ^ l = G b , l θ b , l + g b , l \boldsymbol{\hat{x}}_{l} = G^{b,l} \boldsymbol{\theta}^{b,l} + g^{b,l} x^l=Gb,lθb,l+gb,l
我们可以将基本组合块组合起来形成栈,然后再将栈组合起来形成pipeline。关于这部分内容,将在下一篇博文中讲解。
这篇关于时间序列预测的Meta N-BEATS方法1的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







