本文主要是介绍算术平均滤波法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
算术平均滤波法
- 一、C 实现算术平均滤波法及代码详解
- 二、C++ 实现算术平均滤波法及代码详解
- 算法原理
- 代码实现
- 总结
- 三、Java 实现算术平均滤波法及代码详解
算术平均滤波法是一种常用的信号滤波方法,其原理是对连续的一段信号值进行平均处理,以减小信号中的噪声干扰。具体操作方法如下:
-
选取一段连续的信号,一般取3-15个数据点,称为窗口大小。
-
计算窗口内所有数据点的平均值,以该平均值作为滤波后的输出值。
-
将窗口向后平移一位,即将窗口内的数据点右移一位,然后重复第2步操作,直到滤波结束。
算术平均滤波法适用于信号变化缓慢且噪声比较小的情况,可以有效地平滑信号并减小噪声,但对于快速变化的信号或者噪声比较大的情况,则可能会产生较大误差。
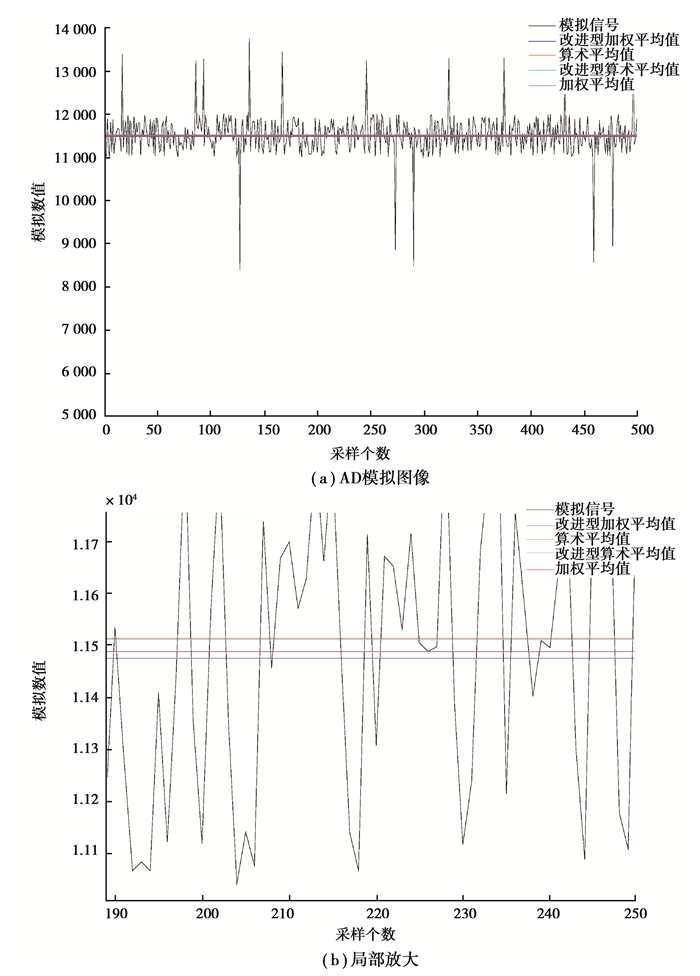
一、C 实现算术平均滤波法及代码详解
算术平均滤波法是信号处理领域中常用的平滑滤波方法之一。它的基本思想是对信号中的每个采样点,取其周围一定数量的采样点的平均值作为该点的输出值。这样可以有效地去除信号中的噪声和抖动,同时保留信号的主要特征。
C语言实现算术平均滤波法的过程如下:
-
定义滤波器窗口的大小:即取信号中每个采样点左右两边各几个点的平均值。一般窗口大小越大,滤波效果越好,但计算量也会增加。
-
读入信号:从外部文件或者传感器获取信号数据。
-
对每个采样点进行滤波:以当前采样点为中心,取左右各窗口大小个采样点的平均值,作为该点的输出值。
-
输出滤波后的信号:将滤波后的信号保存到外部文件或者传感器输出。
下面是算术平均滤波法的C语言代码示例:
#include <stdio.h>#define N 100 // 信号长度
#define W 5 // 窗口大小int main()
{int signal[N]; // 输入信号int output[N]; // 输出信号int sum; // 窗口内信号值的总和// 读入信号for (int i = 0; i < N; i++){scanf("%d", &signal[i]);}// 对每个采样点进行滤波for (int i = 0; i < N; i++){sum = 0;for (int j = i - W; j <= i + W; j++){if (j >= 0 && j < N){sum += signal[j];}}output[i] = sum / (2 * W + 1); // 取窗口内信号值的平均值}// 输出滤波后的信号for (int i = 0; i < N; i++){printf("%d ", output[i]);}return 0;
}
上述代码中,定义了信号长度为100,窗口大小为5。首先读入信号,然后对每个采样点进行滤波,最后输出滤波后的信号。
需要注意的是,在计算窗口内信号值总和时,需要判断窗口是否越界,以避免程序崩溃。
另外,上述代码只是最基本的实现方法,还有很多优化的空间,比如使用滑动窗口、处理边界效应等,可以根据具体应用场景进行进一步优化。
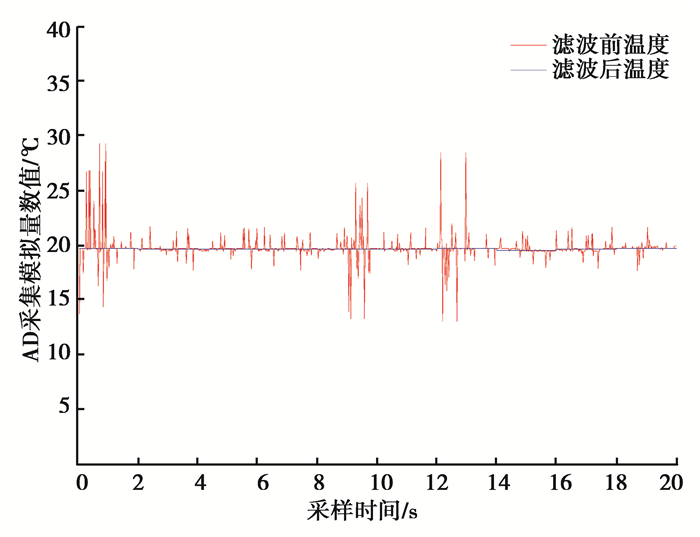
二、C++ 实现算术平均滤波法及代码详解
算术平均滤波法是一种常见的数字信号处理技术,它通过对信号一定数量的采样值进行求和和平均,来减少信号中的随机噪声。在本文中,我们将介绍如何使用 C++ 实现算术平均滤波法,并解释算法的工作原理和代码细节。
算法原理
算术平均滤波法的基本思路是,对信号中的一组采样值进行求和,并将和值除以采样值的数量,得到平均值。如果信号中存在随机噪声,那么平均值应该更接近于信号的真实值,因为随机噪声在整个采样序列中随机分布,对求和的结果影响会被平均掉。
具体而言,算法的步骤如下:
-
确定采样窗口的大小,即需要对多少个采样值进行求和平均。窗口大小可以根据实际需求和信号特性进行调整。
-
将窗口从左到右移动,每次将窗口内的采样值求和,并计算平均值。
-
将平均值作为当前窗口所在位置的输出值,并将窗口向右移动,继续执行步骤 2。
代码实现
下面是使用 C++ 实现算术平均滤波法的代码示例:
#include <iostream>
#include <vector>using namespace std;vector<double> movingAverage(const vector<double>& input, int windowSize) {vector<double> output(input.size() - windowSize + 1);for (int i = 0; i < output.size(); ++i) {double sum = 0.0;for (int j = i; j < i + windowSize; ++j) {sum += input[j];}output[i] = sum / windowSize;}return output;
}int main() {vector<double> input = {1, 2, 3, 3, 2, 1};int windowSize = 3;vector<double> output = movingAverage(input, windowSize);cout << "Input: ";for (auto x : input) {cout << x << " ";}cout << endl;cout << "Output (window size = " << windowSize << "): ";for (auto x : output) {cout << x << " ";}cout << endl;return 0;
}
在上述代码中,movingAverage 函数接受两个参数:输入序列 input 和采样窗口的大小 windowSize。该函数返回一个新的序列 output,其中包含了经过算术平均滤波法处理过后的输入序列。
在 movingAverage 函数中,我们首先创建了一个长度为 input.size() - windowSize + 1 的输出序列 output,用来存储算法的输出值。接下来,我们遍历输出序列中的每一个位置,对当前位置的采样窗口中的值进行求和,计算平均值,并将其作为当前位置的输出值。这样就完成了整个算法的实现。
在 main 函数中,我们定义了一个输入序列 input 和一个采样窗口大小 windowSize,并调用 movingAverage 函数对输入序列进行处理。最后,我们输出了原始输入序列和经过处理后的输出序列,以检验算法的正确性。
总结
算术平均滤波法是一种简单有效的数字信号处理技术,可以帮助我们减少信号中的随机噪声。在本文中,我们介绍了如何使用 C++ 实现算术平均滤波法,并解释了算法的工作原理和代码细节。使用该算法可以对实时或离线的数据进行滤波处理,以提高数据质量和精度。
三、Java 实现算术平均滤波法及代码详解
算术平均滤波法是时间序列信号处理中常用的一种滤波方法,其基本思想就是用一组样本的平均值代替原始信号中的每一个样本值。该滤波方法简单易实现,但对于数据包含的噪声和干扰较多的信号并不适用。
下面是 Java 实现算术平均滤波法的代码及详解:
public class ArithmeticAverageFilter {private int windowSize; // 滑动窗口大小private Queue<Double> queue; // 用队列存储窗口内的数据public ArithmeticAverageFilter(int windowSize) {this.windowSize = windowSize;this.queue = new LinkedList<>();}// 添加新的数据到滑动窗口public void addData(double data) {queue.add(data);if (queue.size() > windowSize) {queue.poll();}}// 计算滑动窗口内数据的平均值public double getAverage() {double sum = 0;for (double data : queue) {sum += data;}return sum / queue.size();}
}
以上是算术平均滤波法的实现代码。该类中包含两个主要的方法,分别是 addData 和 getAverage。
addData 方法用于向滑动窗口中添加新的数据,当滑动窗口的大小超过设定的窗口大小时,队头的数据将被移出队列。
getAverage 方法用于计算滑动窗口内数据的平均值,通过遍历队列内的数据求和并除以队列长度即可得到平均值。
下面是一个使用算术平均滤波法的简单示例:
public class Main {public static void main(String[] args) {double[] data = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};int windowSize = 3;ArithmeticAverageFilter filter = new ArithmeticAverageFilter(windowSize);// 添加数据并输出滤波后的结果for (double d : data) {filter.addData(d);System.out.println(filter.getAverage());}}
}
在上述示例中,首先定义了一个长度为 10 的数组作为原始数据,窗口大小设置为 3。然后通过循环依次向滑动窗口中添加数据,并调用 getAverage 方法计算平均值并输出到控制台上。
运行结果如下:
1.0
1.5
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
可以看到,经过滤波后的结果平滑了许多,但同时也存在着一定程度的信号失真问题。因此,在实际应用中需要选择合适的滤波方法以及参数,以达到滤波效果与信号质量的平衡。
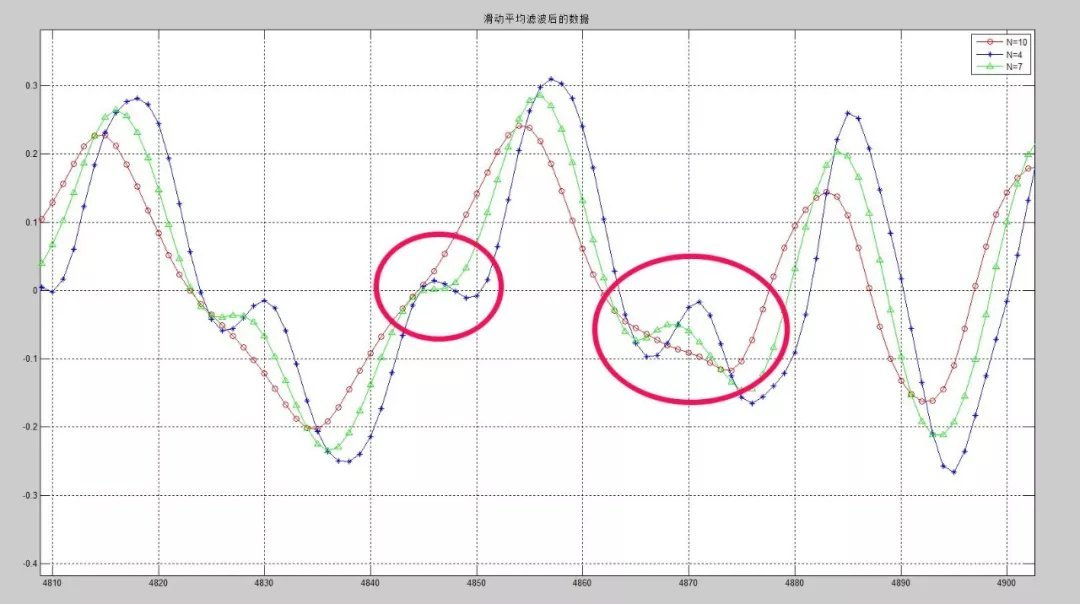
这篇关于算术平均滤波法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








