本文主要是介绍高等数学 下册 错题集，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
| 题目 | 答案 |
|---|---|
| 若 ∑ a n \sum an ∑an收敛于a，则= ∑ a n − a n + 1 = ? \sum a_n-\mathfrak{a}_{\mathrm{n+1}}=? ∑an−an+1=? | ∑ a n \sum an ∑an收敛于a -> an=0 -> ∑ a n - a n + 1 = − a n + a 1 = a 1 \sum a_n\text{ - a}_{\mathrm{n+1}}\mathrm{=-an+a1=a1} ∑an - an+1=−an+a1=a1 |
| ∑ a n \sum an ∑an收敛是 ∑ a n 2 \sum an^2 ∑an2收敛的条件 | 不充不必 反例 1/n 和 1 ( − 1 ) n 1 n 3 1(-1)^{\mathrm{n}}\frac1{\sqrt[3]{n}} 1(−1)n3n1 |
| 若 ∑ ( ln a ) n \sum\left(\ln a\right)^n ∑(lna)n收敛，求a范围 | x n \mathrm{x}^n xn收敛， x ∈ ( − 1 , 1 ) \mathrm{x\in(-1,1)} x∈(−1,1)所以， a ∈ ( 1 e , e ) \mathfrak{a}\in(\frac1e,e) a∈(e1,e) |
| F ( x , y ) = { 0 , x + y = 0 ( x 2 − 3 y 2 ) / ( x + y ) , x + y ≠ 0 \mathrm{F(x,y)=}\left\{\begin{aligned}&0,&\mathrm{x+y=0}\\&(x^2-3y^2)/(x+y),&\mathrm{x+y\neq0}\end{aligned}\right. F(x,y)={0,(x2−3y2)/(x+y),x+y=0x+y=0，问 F ′ y ( 0 , 0 ) = ? \mathrm{F'}_\mathbf{y}(0,0)=? F′y(0,0)=? |  |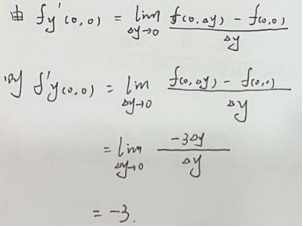
| F ( x , y ) = { 0 , x + y = 0 ( x 2 − 3 y 2 ) / ( x + y ) , x + y ≠ 0 \mathrm{F(x,y)=}\left\{\begin{aligned}&0,&\mathrm{x+y=0}\\&(x^2-3y^2)/(x+y),&\mathrm{x+y\neq0}\end{aligned}\right. F(x,y)={0,(x2−3y2)/(x+y),x+y=0x+y=0，哪些点上函数连续 |  |
 |  |
 |  |
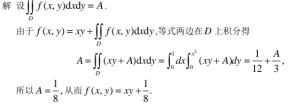| 判别级数敛散性 ∑ n = 1 ∞ ( − 1 ) n ln ( 1 + 1 n ) \sum_{n=1}^{\infty}(-1)^{n}\ln(1+{\frac{1}{\sqrt{n}}}) ∑n=1∞(−1)nln(1+n1) |  |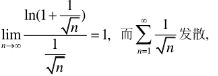
| 幂函数转换记得定义域转换和函数，记得 ∑ \sum ∑ 下面是n=0还是n=1，决定了a1 | |
 |  |
 |  |
 |  |
 |  |
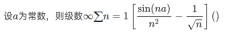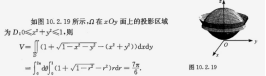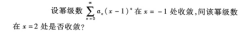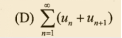| 为什么不收敛 ∑ n = 1 ∞ ( − 1 ) n u n n \sum_{n=1}^\infty(-1)^n\frac{u_n}n ∑n=1∞(−1)nnun 和 ∑ n = 1 ∞ ( u 2 n − 1 − u 2 n ) \sum_{n=1}^{\infty}(u_{2n-1}-u_{2n}) ∑n=1∞(u2n−1−u2n) | 取 u n = ( − 1 ) n ln ( n + 1 ) u_{n}=\frac{(-1)^{n}}{\ln(n+1)} un=ln(n+1)(−1)n 和 u n = ( − 1 ) n − 1 n u_n\quad=\quad\frac{(-1)^{n-1}}n un=n(−1)n−1 |
| lim n → ∞ n 1 / n = 1 \lim_{n\to\infty}n^{1/n}=1 limn→∞n1/n=1 | 法一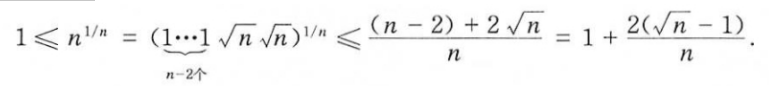： 法二： n 1 n = e n ln n \mathrm{n}^{\frac1n}=e^{n\ln n} nn1=enlnn |
 |  |
 |  |
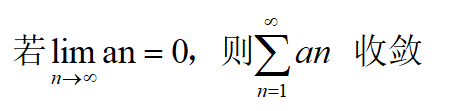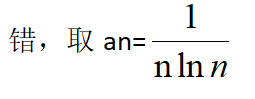| 判断级数 1 n ln n \frac1{n\ln n} nlnn1的敛散性 |  |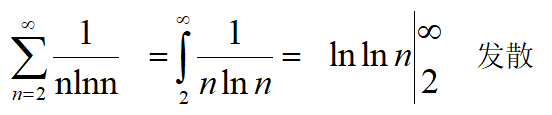
 |  |
 |  |
 |  |
 |  |
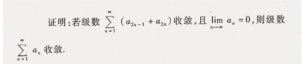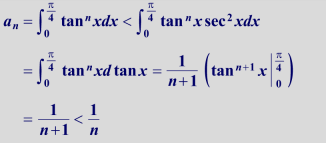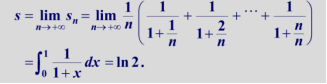作者一言：
- 这是两年前的笔记，所以，如果你们有相关的问题，可以发在评论区等善良的有缘人来给你们解答。（因为我不会）
- 因为当时写笔记的时候用的是本地文档，当时使用的是unicode公式，而csdn使用的latex公式格式，所以文中出现的非图片的公式，是经过公式识别后插入的，贴上来的时候我有检查过一遍，但是如果你们发现哪里有缺少公式或者错误，可以在评论区@我。
这篇关于高等数学 下册 错题集的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
