本文主要是介绍高等数学 下册 错题集2,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
椭圆抛物面 x 2 2 p + y 2 2 q = z ( p 与 q 同号) \frac{x^2}{2p}+\frac{y^2}{2q}=z (p与q同号) 2px2+2qy2=z(p与q同号)
椭球面 x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 a2x2+b2y2+c2z2=1
单叶双曲面 x 2 a 2 + y 2 b 2 − z 2 c 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1 a2x2+b2y2−c2z2=1
二次锥面 x 2 a 2 + y 2 b 2 − z 2 c 2 = 0 \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0 a2x2+b2y2−c2z2=0
| 2xy <= x2+y2 Xy转化为 x2+y2 (要用<=,因为x2+y2/xy极限不存在) |
| 2xy <= x2+y2 |
| Xy转化为 x2+y2 >= 1 |
| xy 转化为 x2+y2 |
| 证明:极限不存在 解:随k变化而变化/y不同时,极限取值不同 |


偏导数定义
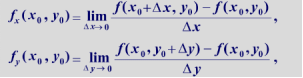
全微分定义
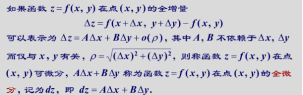

近似数(偏增量 偏微分·△x)

全增量:

几点说明:

偏导数几何意义
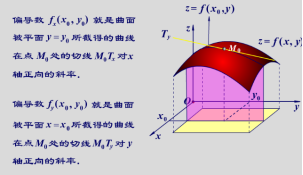
偏导数经济学意义:

需求对价格的偏弹性: − ∂ Q ∂ P ⋅ P Q -\frac{\partial Q}{\partial P}\cdot\frac{\mathrm{P}}{\mathrm{Q}} −∂P∂Q⋅QP
相对误差和绝对误差:

易混淆
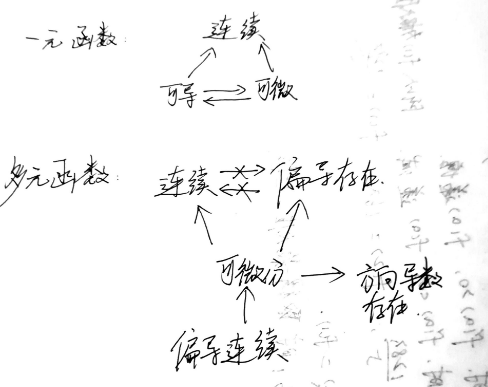
内点,外点,边界点
1、内点指的是存在一个该点的领域被包含在所给点集,则称该点是该点集的内点
2、外点指的是存在一个该点的领域完全在所给点集之外,则称该点为外点。
3、边界点指的任做该点的领域,领域内都同时有外点和内点,则称该点为边界点;聚点则是对边界点和内点的统一定义。
开集,闭集,连通集
内点组成开集
余集组成开集 的集合成为闭集
非开集也非闭集:没有包括所有的外点和所有的边界点。
导集:聚点的合集
连通,则(开)区域,开区域+边界=闭区域
以O为圆心的圆称为 K。如果E包含于K,则E有界集
聚点
聚点定义是设E的全集为S,若点P属于S,且点P的任一个去心邻域与E的交集非空,则称P为E的一个聚点。
内点一定是聚点,但聚点不一定是内点,聚点可能还包含边界点以及不属于E的极限点。
补充一个例子
A=(1,3)-{2},则A的聚点为[1,3],此时2也是A的聚点,但2不属于A。
集合E的聚点就是极限点,定义是包含该点的任意小球(或邻域)内都包含E的无限多个点.
例如:
1、康托集合(Cantor set)的所有的点都是聚点.
2、S是区间[2,3]中的有理数,则[2,3]中的所有点都是聚点.
3、集合[0,1]与{1.5}的并集的聚点是[0,1]的所有点,但不包括1.5该点.
4、区间(1,2)的聚点是[1,2]中的所有点.
以上例子中,例1和例2的集合根本不存在内点,所有的聚点都是它的边界点.例3中包含了所有内点,却没有包含边界点1.5;而例4中包含了所有的内点与边界点.
从以上例子中容易看出,开区间的端点是聚点,但是不属于该区间;一个稠密的集合中,非常容易找出不属于该集合的聚点(例2中的无理数).
站在开集中的任何一个位置,往任何方向走任意充分小的距离,你仍然在开集内。 如果你站立的位置在集合中且满足:往任何方向走任意充分小的距离仍然在集合内,那么你就在这个集合的内部,你所处的位置就是集合的内点。显然,集合为开集等价于集合中每个点都是内点,集合的内部由集合所有的内点组成。 全集挖去开集的剩余部分就是闭集。也就是说,你站在闭集外的任意一个点上,往任意方向走任意充分小的距离仍然在闭集外。如果你站立的位置在集合外且满足:往任何方向走任意充分小的距离仍然在集合外,那么你就在集合的外部,你所处的位置就是集合的外点。显然,集合的外部由集合所有的外点组成。且集合的补集的内点就是集合的外点。 那么在全集中,除去集合内部,集合外部,剩下的点组成的集合就是集合的边界。容易发现,站在集合的边界上一个确定的点处朝着一个方向走任意取定的距离。随着方向的改变,你既有可能走到集合内一点处又有可能走到集合外一点处。这与“边界”这个词本身的含义是吻合的。 那么开集能包含边界中点吗?不能!如果包含了边界中点,那么我们从那个点出发朝某个方向走充分小的距离就能走到集合外一点处,与开集定义矛盾。 那么闭集要包含边界中所有点吗?是的!如果存在边界上的点在闭集之外,从那个点出发朝某个方向走充分小的距离就能走到集合内一点,与闭集定义矛盾! 那么反过来,如果集合包含自身的所有边界点一定是闭的吗?是的!因为全集中的所有点一共只有三种类型:这个集合的内点、外点、边界点。考虑这个集合外一点,其不可能为边界点,也不可能为内点,故必定为外点,满足闭集定义 |
这篇关于高等数学 下册 错题集2的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!












