本文主要是介绍黎曼几何与切空间之间的投影,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
公式:
从黎曼空间投影到切空间,其中P为黎曼均值,也是切空间的参考中心点,Pi是要投影到切空间的点。
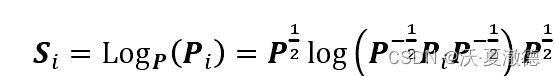
从切空间投影回来,其中Si为切空间中的向量。
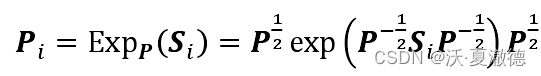
function Tcov = CovToTan(cov,Mcov)Cm12 = Mcov^(-1/2);X_new = logm(Cm12 * cov * Cm12);C12 = Mcov^(1/2);Tcov = Mupper(C12 * X_new * C12);
endfunction Cov = TanToCov(vec,Mcov)X = Munupper(vec);Cm12 = Mcov^(-1/2);X = Cm12 * X * Cm12;C12 = Mcov^(1/2);Cov = C12 * expm(X) * C12;
endfunction T = Mupper(X)% Upper triangular part vectorization with diagonal preservation.% This function keeps the upper triangular part of the matrix and% vectorizes it while multiplying non-diagonal elements by sqrt(2).% Get the size of X[M, N] = size(X);% Check if matrices are squareif M ~= Nerror('Matrices must be square');end% Initialize T with zerosT = zeros(M, M, 'like', X);% Calculate the multiplier for non-diagonal elementsmultiplier = sqrt(2);% Fill T with the upper triangular part, preserving the diagonalfor i = 1:Mfor j = i:Mif i == jT(i, j) = X(i, j); % Diagonal element remains the sameelseT(i, j) = X(i, j) * multiplier; % Non-diagonal elements multiplied by sqrt(2)endendend% Flatten the upper triangular part of T to a vectorT = T(triu(true(size(T))) == 1);T = T';
endfunction X = Munupper(T, n)% Reverse the operation to reconstruct the matrix from its upper triangular part.% Calculate the size of the square matrix based on the length of the input vector Tn = round((sqrt(1 + 8 * length(T)) - 1) / 2);% Check if T is a valid upper triangular vectorm = n * (n + 1) / 2;if numel(T) ~= merror('Invalid input. Input vector size does not match the expected size for upper triangular vectors.');end% Initialize the symmetric matrix X with zerosX = zeros(n, n, 'like', T);% Calculate the indices for the upper triangular part[I, J] = find(triu(ones(n)));% Reverse the vectorization and apply the appropriate scaling to non-diagonal elementsfor k = 1:numel(I)i = I(k);j = J(k);if i == jX(i, j) = T(k); % Diagonal elements remain the sameelseX(i, j) = T(k) / sqrt(2); % Reverse scaling for non-diagonal elementsX(j, i) = X(i, j); % Symmetric matrixendend
end这篇关于黎曼几何与切空间之间的投影的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





