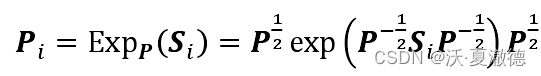文章目录 黎曼引理、黎曼-勒贝格引理Riemann引理Riemann-Lebesgue引理 本篇文章适合个人复习翻阅，不建议新手入门使用 黎曼引理、黎曼-勒贝格引理 Riemann引理 我们知道一般情况下积分算子是无法保持乘法的，即 ∫ a b f ( x ) ⋅ g ( x ) d x ≠ ∫ a b f ( x ) d x ⋅ ∫ a b g ( x ) d x

公式： 从黎曼空间投影到切空间，其中P为黎曼均值，也是切空间的参考中心点，Pi是要投影到切空间的点。  从切空间投影回来，其中Si为切空间中的向量。 function Tcov = CovToTan(cov,Mcov)Cm12 = Mcov^(-1/2);X_new = logm(Cm12 * cov * Cm12);C12 = Mcov^(1/2);Tcov = Mupper(

笔者通过观察黎曼积分相关定理、定义的结构，发现其和序列定义的相似性。于是最终成功构造出了一个和黎曼积分等价的序列-胡杰黎曼序列，通过该序列就能证明，黎曼积分的所有定理、性质、甚至是定理的证明，都可以被归约为序列极限相关的性质证明 本文编写于14日精读掌握《陶哲轩:实分析》,day12,2019/7.19