球体的顶点绘制与纹理坐标的转换

本文主要是介绍球体的顶点绘制与纹理坐标的转换，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

预备知识：基础三角函数sin 、cos、方位角、仰角

方位角：the angular distance usually measured clockwise from the north point of the horizon to the intersection with the horizon of the vertical circle passing through a celestial body — from WiseDictionary
意思就是说水平圆片的角 $\theta$ 范围是从0~2π
仰角：在视线所在的垂直平面内，水平线以上的视线与水平线所形成的夹角 $\phi$

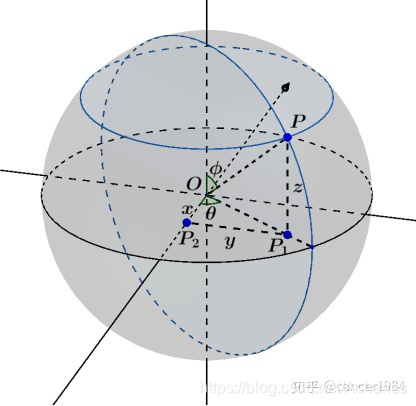
在这里插入图片描述
在该图片中，x轴指向屏幕外，与y轴垂直，Z轴指向上方。且线段|PO| = R

即：R* cos( $\phi$ ) = z;
R* sin( $\phi$ ) = |OP1| （注P1为点P在圆形平面xoy 上的垂点）
沿着P1作线段垂直x轴于P2，

 线段|P1P2|就是y, |OP2|就是x
|p1p2| = y
|Op2| = x

对于球上一点P(x,y,z),;

$\begin{cases} R*sin(theta)*cos(phi), \\ R*sin(theta)*sin(phi), \\ R*cos(theta) \end{cases}$

最后需要注意点：在一般的生活中，x轴指向屏幕外，与y轴垂直，Z轴指向上方，这并不奇怪。但在图形学中，通常是Z轴指向屏幕里面，我们看到的2D平面（屏幕）是横轴X向右为正，纵轴Y向下为正。

球体3D坐标轴与2D纹理顶点数据

在上述公式中决定P（x, y, z）的只有R（默认为1.0f）和 $\theta$ 角以及 $\phi$ 。
绘制一个球体的过程在代码中总是从下到上，一层一层地绘制出“点圈”，数层点圈紧密叠在一起就成了一个球体。我们将抽象成两个变量：1、一个y轴上线性递增的量ySegment 2、一个围绕不同维度画一个圈的周长长度的变量xSegment。

如果我们想要将一张2D的图片映射到3D的球面上，那么就必须保持2D图片坐标(U, V)与(xSegment, ySegment)对应即可。

也就是说当设定好xSegment和ySegment的增长率，这里假设为a,b;
那么就可以有：
U = xSegment = xstep * a ; (比如，a = 1/50，将周长均匀划分50等分 )
V = ySegment = ystep * b; (比如， b = 1/50，将球的高度均匀划分50等分)

附带C++实现球体3D坐标到2D纹理坐标的代码：

	const float R = 1.0f;for (int y = 0; y <= Y_SEGMENTS; y++){for (int x = 0; x <= X_SEGMENTS; x++){float xSegment = (float)x / (float)X_SEGMENTS;float ySegment = (float)y / (float)Y_SEGMENTS;float xPos = std::cos(xSegment * 2.0f * PI) * std::sin(ySegment * PI);float yPos = std::cos(ySegment * PI);float zPos = std::sin(xSegment * 2.0f * PI) * std::sin(ySegment * PI);sphereVertices.push_back(xPos);sphereVertices.push_back(yPos);sphereVertices.push_back(zPos);// xSegment. ySegment就是对应的纹理坐标纹理//同样压入顶点序列sphereVertices.push_back(xSegment);sphereVertices.push_back(ySegment);}}