本文主要是介绍数学建模--关于长江三角洲区域一体化高质量发展问题 问题二求解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文记录数学建模A题--关于长江三角洲区域一体化高质量发展问题,问题二模型的建立与求解。
https://blog.csdn.net/a202105570626/article/details/132046958?spm=1001.2014.3001.5501
数学建模--关于长江三角洲区域一体化高质量发展问题 问题一求解_nap-joker的博客-CSDN博客
数学建模--关于长江三角洲区域一体化高质量发展问题 问题一投影寻踪法_nap-joker的博客-CSDN博客
目录
基于K-MEANS算法的城市群分类模型
模型的建立
K-MEANS算法的求解
分类结果的合理性及敏感性分析
模型的合理性分析
模型的敏感性分析
基于K-MEANS算法的城市群分类模型
问题二的流程图如下所示:
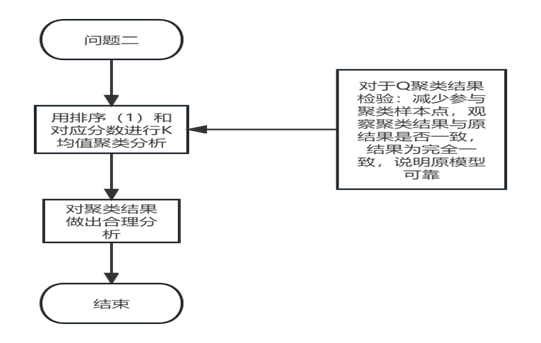
模型的建立
为了研究长江三角洲城市群高质量发展水平状况,本文根据问题一利用TOPSIS法得出的各个城市生态环境等三个一级指标的得分和综合得分,建立K-Means聚类模型,并利用肘部法则确定聚类的类别个数。最终,将长江三角洲城市群划分为3个类别。K-means算法的处理流程如下所示:
Step1:利用肘部法则确定聚类类别数
K-means聚类算法中,肘部法则的基本原理是通过计算不同簇数下的聚类误差平方和来确定最佳的簇数。其中,聚类误差平方和是指每个数据点与其所属簇的中心点之间的距离平方和。随着簇数的增加,距离平方和会逐渐减小,但与此同时,减小的速度会趋缓。肘部法则即通过“坡度趋于平缓”找出最佳的簇数。
经计算,绘制距离平方和和聚类个数的面积图,如下所示:
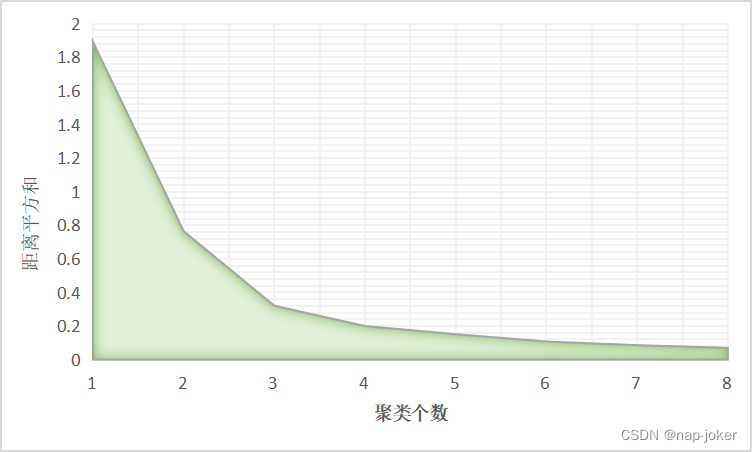
如上图所示,发现坡度在聚类个数达到3以后逐渐趋于平缓,故本文认为聚类簇数为3。
Step2:从数据集中随机选取3个对象作为初始聚类中心c1,c2,c3.
Step3:逐个将对象xi(i=1,2,...,27.) 按欧式距离分配给距离最近的一个聚类中心cj,1≤j≤3. 其中,距离计算公式为:
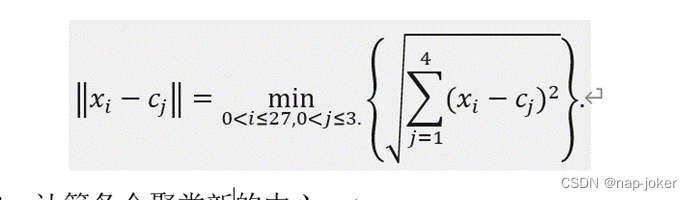
Step4:计算各个聚类新的中心
计算公式为:
其中,是第j个聚类
中所包含的对象个数。当聚类中心不再发生变化时,目标函数最小,此时即得到最优结果。
K-MEANS算法的求解
本文采用上述的K-MEANS聚类算法,将长江三角洲城市群的27个城市划分为3个类别,如下表所示:
| 类别 | 城市 |
| 类别一 | 温州、无锡、台州、合肥、宁波、南京、杭州、苏州 |
| 类别二 | 上海 |
| 类别三 | 池州、宣城、铜陵、马鞍山、安庆、滁州、泰州、扬州、芜湖、湖州、镇江、盐城、晶华、舟山、嘉兴、绍兴、常州、南通 |
由上表可知,各类别城市分布不均匀,三个类别分别有8,1,18个城市。第二个类别仅仅含有上海一个城市。绘制三维饼图,如下所示:
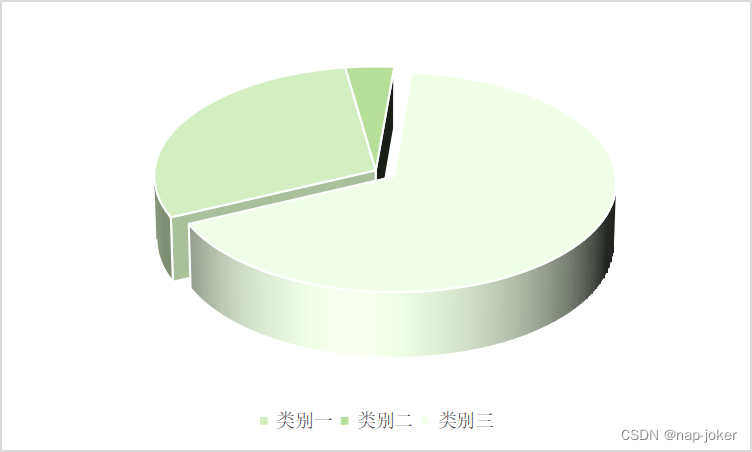
各个聚类类别的中心点坐标如下所示:
| 聚类种类 | 生态环境 | 社会与民生 | 经济增长 | 综合得分 |
| 1 | 0.4154298678613674 | 0.3052284737916807 | 0.3155021292182527 | 0.3186755653932306 |
| 2 | 0.70154948758922 | 0.635647103146899 | 0.866852490021937 | 0.759918944876179 |
| 3 | 0.3672572897681001 | 0.11182194618350431 | 0.1471709287248632 | 0.1489483950216382 |
对各个类别的聚类中心进行分析,发现类别二的城市群具有综合得分高,生态环境、社会与民生以及经济增长三方面均衡发展且发展态势较好的特点。但也存在着“郊区发展缓慢滞后,发展水平摊薄”、“生活成本过高,阻碍转向创新驱动”等短板。类别一的城市综合发展水平较类别三的城市综合发展水平高,经济增长和社会与民生这两方面发展相对比较均衡,但是经济增长和社会与民生这两方面的得分低于生态环境的得分。类别三的城市综合发展水平最低,其生态环境这一指标的得分远远高于另两个指标的得分。故,本文认为类别二的城市代表着长三角城市群发展水平高的梯队,类别一的城市代表着发展水平中等的梯队,类别三的城市代表着发展水平较低的梯队。
从三个类别聚类中心的生态环境等三个指标的取值也能发现,经济的增长能够推动生态环境的保护和社会与民生的发展。三个指标的变化态势趋同。对于一个城市的发展,经济水平的提高固然很重要,与此同时,生态环境的保护也不可或缺,社会与民生的管理也处于重要地位,三者需协同发展。
分类结果的合理性及敏感性分析
模型的合理性分析
本文使用
轮廓系数、DBI和CH这三个指标对K-Means聚类的结果进行评价。其中,轮廓系数的取值范围为[-1,1],当同类别样本距离越相近二不同类别样本距离越远时,轮廓系数的取值愈接近1,代表着聚类效果越好。DBI指数用来衡量任意两个簇的簇内距离和簇间距离之比,该指标越小表示着聚类效果越好。CH值由分离度和紧密度的比值得到,CH越大表示聚类效果越好。
经计算,得模型的评价指标如下所示:
| 轮廓系数 | DBI | CH |
| 0.524 | 0.533 | 58.925 |
由上表可知,该聚类模型的效果较好。其轮廓系数取值为0.524,接近于1,DBI指数取值为0.533,相对较小,CH的取值为58.925,数值较大。综上,在一定程度上能够认为上述的K-Means聚类算法的效果较好,能够对长江三角洲城市群的高质量发展状况进行合理的分类。
模型的敏感性分析
模型的敏感性分析需要从定量分析的角度研究有关因素发生某种变化对某一个或者一组关键指标影响程度的一种不确定分析技术[6]。本文通过对长江三角洲城市群进行扰动处理,即随机性增加或减少一两个城市,来判断是否会对模型的分类结果造成影响,进而对模型的敏感性进行分析。
通过给城市群随机进行扰动,分析影响分类结果与否,可以得到如下表所示结果(仅展示前4个城市数据)。
| 随机去除两个样本点后聚类 | 综合得分 | 原始聚类 |
| 类别2 | 0.759918945 | 类别2 |
| 类别1 | 0.363689309 | 类别1 |
| 类别1 | 0.262764633 | 类别1 |
| 类别3 | 0.192524304 | 类别3 |
从表中可以看出,对长江三角洲城市群随机去除两个城市数据后再进行聚类的结果和原始的聚类结果是一致的,这在一定程度上可以说明,小范围内的数据变化并不会对城市高质量发展状况的分类结果产生影响,由此可以说明本文使用的K-Means聚类算法的敏感性良好。
这篇关于数学建模--关于长江三角洲区域一体化高质量发展问题 问题二求解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







