本文主要是介绍数学建模--关于长江三角洲区域一体化高质量发展问题 问题一投影寻踪法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文记录数学建模A题--关于长江三角洲区域一体化高质量发展问题,这一题目问题一基于遗传算法优化求解的投影寻踪法模型的建立与求解过程。对于整个问题的初步分析和基于TOPSIS法的问题一求解过程可参看上两篇文章。
数学建模--关于长江三角洲区域一体化高质量发展问题 问题一求解_nap-joker的博客-CSDN博客
数学建模--关于长江三角洲区域一体化高质量发展问题 初步分析_nap-joker的博客-CSDN博客
目录
基于投影寻踪法的发展水平评价模型
模型的建立
模型的求解
基于斯皮尔曼相关性分析的评价模型检验
基于投影寻踪法的发展水平评价模型
本文选择了64个综合评价指标来量化长江三角洲城市群的高质量发展水平的高低,由于各个指标对于评价发展水平的贡献程度不同,同时各个指标之间有着直接或者间接的联系,并不相互独立,为了更加客观、科学地进行评价,本文选择投影寻踪法进行评价。
模型的建立
投影寻踪法是一种处理和分析高维数据的统计方法,其基本思想是将高维数据向低维子空间上,进而寻找出反映原始高维数据的特征或者结果的投影值,以便于达到研究和分析高维数据的目的。该模型能够提高了综合评价以及各个层次的分辨能力和评价模型的精度。本文选取了64个三级指标,维度较高,比较适用于适用投影寻踪法进行长江三角洲城市群高质量发展水平的综合评价。
基于投影寻踪法的长江三角洲城市群高质量发展水平的评价模型建立的具体步骤如下:
Step1:线性投影
从不同的方向或角度取观察数据,寻找最能够充分性反映指标数据特征的最优投影方向。随机性的抽取若干个初始投影方向α=a1,a2,...,a64, 计算其投影指标的大小,之后确定最大指标投影的解为其最佳投影方向。则第i个样本在一维线性空间的投影特征值ui 的表达式为:

Step2:构造投影指标函数
由于对于最优投影方向的定义并不全然相同,本文中希望投影特征的分布满足以下两个要求:
- 1.局部的投影点尽可能的密集;
- 2.投影点团在整体上尽可能散开。
其中,
为投影特征值间的距离,R为估计局部三点密度的窗宽参数,f为阶跃信号。
- 为了满足以上两个要求,本文构造如下所示的目标函数:
- 其中,
为投影特征值的标准差,
为投影特征值的局部密度,两个变量相应的计算公式为:
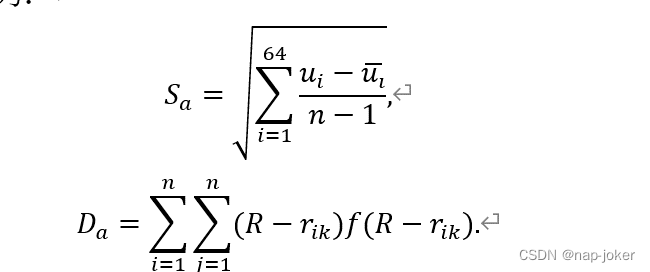
- Step3:优化投影方向
- 综上所示,本文得到一个非线性的优化模型,但该模型较为复杂,为此,本文选用遗传算法优化求解过程。
- Step4:求解投影评价值
- 利用求解所得的最佳投影方向计算样本的投影指标值:
- 其中,最佳投影方向向量即为权重向量,投影指标值即为最终综合评价得分。
-
模型的求解
-
迭代100次遗传算法优化函数,得到了最优投影向量,之后获得长江三角洲城市群27个城市的最终综合评价得分。如下表所示:
-
城市
综合评分
排名
上海
646.7380143
1
苏州
381.7676021
2
杭州
359.9977861
3
南京
312.1511375
4
…
…
…
马鞍山
82.56730566
24
宣城
77.79290636
25
铜陵
60.94706787
26
池州
59.88349746
27
- 由上表可知,投影寻踪法和TOPSIS法的求解结果较为类似,上海市的综合得分远超于其余26个城市的综合得分,呈现出“一枝独秀”的态势。与此同时,其他各个城市的发展差距也较大,不均衡。城市综合评价得分最低的为池州,得分仅为59.88349746,远远低于苏州、杭州、南京等排名较前的城市的得分。
-
- Step4:求解投影评价值
- 综上所示,本文得到一个非线性的优化模型,但该模型较为复杂,为此,本文选用遗传算法优化求解过程。
- Step3:优化投影方向
基于斯皮尔曼相关性分析的评价模型检验
为了检验上述评价模型的合理性,本文对TOPSIS法和投影寻踪法的城市排名,即定序数据进行斯皮尔曼相关性分析,来判断两种模型的求解结果是否存在统计上的显著关系(P<0.05)。检验的相关系数表如下所示:
| TOPSIS排名 | 投影寻踪排名 | |
| TOPSIS排名 | 1(0.000***) | 0.966(0.000***) |
| 投影寻踪排名 | 0.966(0.000***) | 1(0.000***) |
由上表可知,由上表可知,投影寻踪法排名和TOPSIS法排名的斯皮尔曼相关系数为0.966,大于0.9,P值为0.000***,其中***代表着1%的显著性水平。综上,可以认为投影寻踪法排名和TOPSIS法排名在统计意义上具有显著相关,两者的结果是基本一致的,这也体现了上述评价模型的合理性,能够有效且准确的对长江三角洲城市群的高质量发展情况进行量化分析。
投影寻踪法的代码为:
clear;clc;
d=[];e=[];
X=xlsread('归一化指标.xlsx',1);
%迭代十次
for k=1:100%数据正向化处理N=800;Pc=0.8;Pm=0.2;M=10;Ci=7;n=64;DaiNo=2;ads=1;%调用遗传算法求解[a1,b1,ee]=RAGA(X,N,n,Pc,Pm,M,DaiNo,Ci,ads);d=[d,a1];e=[b1;e];
end
[a2,b2]=max(d);
%得到各指标权重
e1=e(b2,:);
%得到评分
ff=X*e1';
% xlswrite('指标选取.xlsx',ff',1,'I2:I403');
function [a,b,mmin,mmax]=RAGA(xx,N,n,Pc,Pm,M,DaiNo,Ci,ads)
% N 为种群规模,Pc 为交叉概率,Pm 为变异概率,DaiNo 为了在进行两代进化之后加速一次而 设定的限制数
% n 优化变量数目, M 变异方向所需要的随机数, Ci 为加速次数,xmin 为优化变量的下限 向量,xmax 为优化变量的上限向量
% 变量的数目 n 必须等于 xmin 和 xmax 的维数;ads 为 0 是求最小值,为其它求最大值。 % mmin 和 mmax 为优秀个体变化区间的上下限值if ads==0ad='ascend';elsead='descend';end
% ======================step1 生成初始父代==================================mm1=zeros(1,n);mm2=ones(1,n);for z=1:Ci %表示加速次数为 20 次for i=1:Nwhile 1==1for p=1:n %p 为优化变量的数目,bb(p)=unifrnd(mm1(p),mm2(p));endtemp=sum(bb.^2);a=sqrt(bb.^2/temp);y=Feasibility(a);if y==1v(i,:)=a;break;endendendend
% step1 endfor s=1:DaiNo
% step2 计算适应度for i=1:Nfv(i)=Target(xx,v(i,:));end
%按适应度排序[fv,i]=sort(fv,ad);v=v(i,:);
%step2 end
%step3 计算基于序的评价函数arfa=0.05;q(1)=0;for i=2:N+1q(i)=q(i-1)+arfa*(1-arfa)^(i-2);end
%step3 end
%step4 选择操作for i=1:Nr=unifrnd(0,q(N+1));for j=2:N+1if r>q(j-1) & r<=q(j)vtemp1(i,:)=v(j-1,:);endendend
%step4 end
%step5 交叉操作while 1==1CrossNo=0;v1=vtemp1;for i=1:Nr1=unifrnd(0,1);if r1 < PcCrossNo=CrossNo+1;vtemp2(CrossNo,:)=v1(i,:);v1(i,:)=zeros(1,n);endendif CrossNo~=0 && mod(CrossNo,2)==0break;elseif CrossNo==0 ||mod(CrossNo,2)==1vtemp2=[];endendshengyuNo=0;for i=1:Nif v1(i,:)~=zeros(1,n)shengyuNo=shengyuNo+1;vtemp3(shengyuNo,:)=v1(i,:);%vtemp3 表示选择后剩余的父代endend
%随机选择配对进行交叉操作for i=1:CrossNor2=ceil(unifrnd(0,1)*(CrossNo-i+1));vtemp4(i,:)=vtemp2(r2,:);vtemp2(r2,:)=[];end
%=====================随机配对结束,按顺序 2 数为一对==========================for i=1:2:(CrossNo-1)while 1==1r3=unifrnd(0,1);v20(i,:)=r3*vtemp4(i,:)+(1-r3)*vtemp4(i+1,:);v20(i+1,:)=(1-r3)*vtemp4(i,:)+r3*vtemp4(i+1,:);temp1=sum(v20(i,:).^2);temp2=sum(v20(i+1,:).^2);v2(i,:)=sqrt(v20(i,:).^2/temp1);v2(i+1,:)=sqrt(v20(i+1,:).^2/temp2);if Feasibility(v2(i,:))==1 && Feasibility(v2(i+1,:))==1break;endendend
%step5 endv3=[vtemp3;v2]; %合并交叉部分和剩余部分
%step6 变异操作while 1==1MutationNo=0;v4=v3;for i=1:Nr4=unifrnd(0,1);if r4<PmMutationNo=MutationNo+1;vtemp5(MutationNo,:)=v4(i,:);v4(i,:)=zeros(1,n);endendif MutationNo~=0break;endend
%选择进行变异操作的父代结束shengyuNo1=0;for i=1:Nif v4(i,:)~=zeros(1,n)shengyuNo1=shengyuNo1+1;vtemp6(shengyuNo1,:)=v4(i,:);%vtemp6 表示选择后剩余的父代endend
%变异开始DirectionV=unifrnd(-1,1,1,n);for i=1:MutationNotempNo=0;while 1==1tempNo=tempNo+1;v5(i,:)=sqrt(((vtemp5(i,:)+M*DirectionV).^2)./sum((vtemp5(i,:)+M*DirectionV).^2)); y=Feasibility(v5(i,:));if tempNo==200v5(i,:)=vtemp5(i,:);break;elseif y==1break;endM=unifrnd(0,M);endend
%step6 endvk=[v5;vtemp6];v=vk;
%进行两代进化后再进行适应度评价
end
for i=1:Nfv(i)=Target(xx,v(i,:));
end
%根据适应度排序
[fv,i]=sort(fv,ad);
v=v(i,:);
vk=v;
vv=vk(1:20,:); %选取前 20 个为优秀个体
for t=1:nmm1(t)=min(vv(:,t));mm2(t)=max(vv(:,t));mmin(z,:)=mm1;mmax(z,:)=mm2;if abs(mm1-mm2)<=0.00001break;end
end
a=fv(1); %最大函数值
b=vv(1,:); %最大函数值对应的变量值
end
function y=Target(x,a)[m,n]=size(x);for i=1:ms1=0;for j=1:ns1=s1+a(j)*x(i,j);endz(i)=s1;end
%求 z 的标准差 SzSz=std(z);
%计算 z 的局部密度 DzR=0.1*Sz;s3=0;for i=1:mfor j=1:mr=abs(z(i)-z(j));t=R-r;if t>=0u=1;elseu=0;ends3=s3+t*u;endend
Dz=s3;
%计算目标函数值 Q
y=Sz*Dz;
end
function y=Feasibility(a)b=sum(a.^2);if abs(b-1)<=0.00001y=1;elsey=0;end
end经老师点评,本文最后部分的斯皮尔曼相关性检验并不能验证上述两个模型的求解效果好,有可能两个模型的结果都较差。
这篇关于数学建模--关于长江三角洲区域一体化高质量发展问题 问题一投影寻踪法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









