AcWing 149. 荷马史诗（二叉堆、小根堆、Huffman树、C++）

AcWing 149. 荷马史诗

题目地址：https://www.acwing.com/problem/content/151/

题目描述

一部《荷马史诗》中有 n 种不同的单词，从 1 到 n 进行编号。其中第 i 种单词出现的总次数为 wi 。

达达想要用 k 进制串 si 来替换第 i 种单词，使得其满足如下要求:

对于任意的 1 ≤ i,j ≤ n ，i ≠ j，都有：si 不是 sj 的前缀。

现在达达想要知道，如何选择 si，才能使替换以后得到的新的《荷马史诗》长度最小。

在确保总长度最小的情况下，达达还想知道最长的 si 的最短长度是多少？

一个字符串被称为 k 进制字符串，当且仅当它的每个字符是 0 到 k−1 之间（包括 0 和 k−1）的整数。

字符串 Str1 被称为字符串 Str2 的前缀，当且仅当：存在 1 ≤ t ≤ m，使得 Str1 = Str2 [1…t] 。

其中，m 是字符串 Str2 的长度，Str2[1…t] 表示 Str2 的前 t 个字符组成的字符串。

输入输出

第一行输入n、k，分别表示有 n 种单词，需要使用k进制字符串进行替换。
第2 - (n + 1) 行每行输入一个非负整数 wi ，表示第 i 种单词出现的次数。

数据范围

2 ≤ n ≤ 100000,
2 ≤ k ≤ 9
1 ≤ wi ≤ 10^12

输入样例

4 2
1
1
2
2

输出样例

12
2

思路

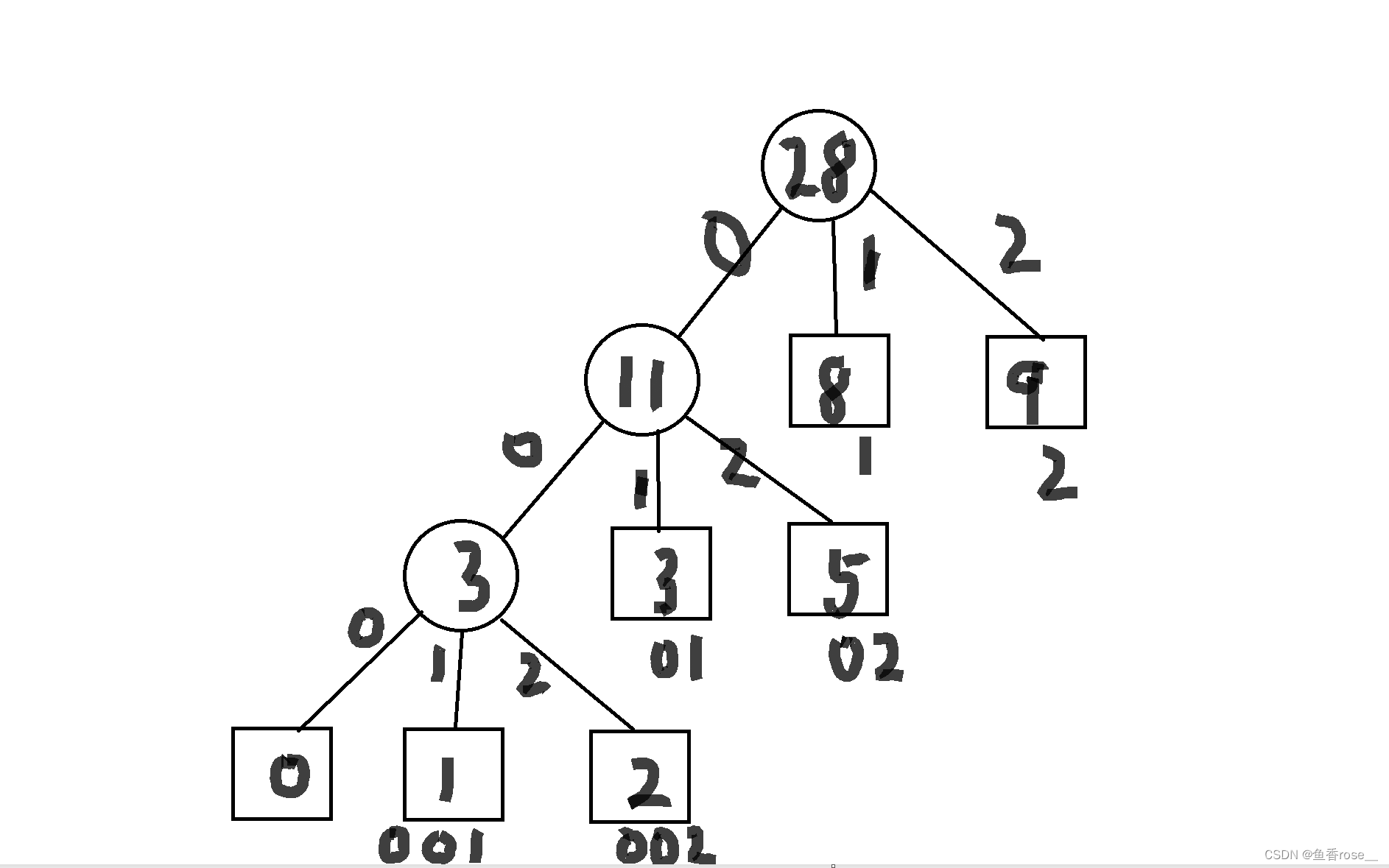
本题所构造的编码方式其实就是 Huffman 编码，我们把单词的出现次数 w1 ~ wn 作为 Huffman 树
叶子节点的权值，然后求出k 叉 Huffman 树。对于 Huffman 树的每个节点的k个分支，分别在边上标
记字符0 ~ k - 1.

此时，可以把这棵Huffman树看作一棵Trie树，就得到了使总长度最小的编码方式——单词 i 的编码就是从根节点到叶子节点 i 的路径上各条边的字符相连。一个单词不是另一个的前缀，其实就对应着： 在Trie树中，所有单词编码的末尾都在叶子节点上，而不在Trie树的一个内部节点上，恰好满足了这个性质。

同时，本题还要求最长的 si 长度最短，我们只需要在求Huffman 树时，对于权值相同的节点，优先考虑当前深度最小（已合并次数最小）的进行合并即可。

哈夫曼树，就是满足权值路径长度最短的树，因此我们这道题目直接可以开哈夫曼树处理即可。

在代码实现过程中，我们先将所有的值压入堆中，每个值的first存的是叶子节点的权值，即单词的出现次数，second存深度。然后，我们在执行上述贪心算法之前，补加一些额外的权值为0的叶子节点，使叶子节点的个数n满足 ( n - 1 ) mod ( k - 1 ) = 0。也就是说，我们让子节点不足k个的情况发生在最底层，而不是根节点处。在满足 ( n - 1 ) mod ( k - 1 ) = 0 时，执行“每次从堆中取出最小的k个权值的贪心算法就是正确的。

C++实现

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>using namespace std;#define IOS ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
#define ll long long
#define endl '\n'typedef pair<ll, ll> pir;	//first存的是叶子节点的权值，即单词的出现次数，second存深度
const int mod = 0x7f7f7f7f;
const int N = 100010;ll a[N], min_len;
priority_queue<pir, vector<pir>, greater<pir> > heap;int main(void){IOSint n, k; cin >> n >> k;for(int i = 1; i <= n; i ++ ){ll x; cin >> x;heap.push({x, 0});}while((heap.size() - 1) % (k - 1) != 0){	//补全额外的叶子节点heap.push({0, 0});}while(heap.size() >= k){ll num = 0, deep = -1;for(int i = 1; i <= k; i ++ ){	//每次取出k个最小权值pir p = heap.top();heap.pop();num += p.first;deep = max(deep, p.second);}min_len += num;	//总权值heap.push({num, deep + 1});	//深度 +1}cout << min_len << endl << heap.top().second << endl;	//堆顶的数即为最长字符串的最短长度return 0;
}