SPSS|偏度和峰度|正态性分布检验|实战小练-SPSS学习（1）

本文主要是介绍SPSS|偏度和峰度|正态性分布检验|实战小练-SPSS学习（1），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

学习目的

检验数据集是否服从正态分布。

软件版本

IBM SPSS Statistics 26。

基础数据

一组数据，如：73 76 78 77 82 82 96 76 65 79 63。

实战

数据准备

输入SPSS中，可选择导入或者直接输入，本例中数据量较少，直接输入。
打开软件主界面，点击底部标签， 切换至“变量视图”，输入变量名称，如VAR：

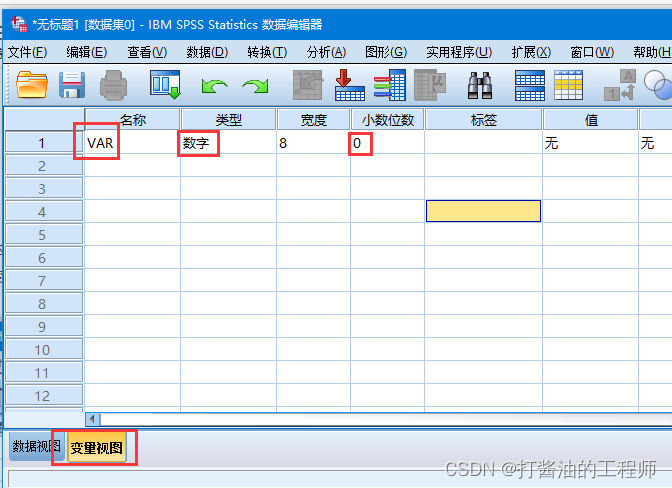
切换到数据视图，输入数据：73 76 78 77 82 82 96 76 65 79 63。

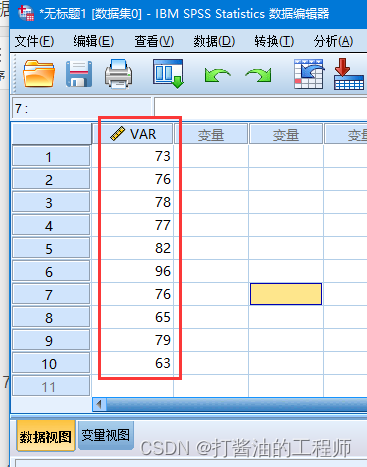
数据初探

完成数据输入后，在主界面依次点击：分析-描述统计-探索

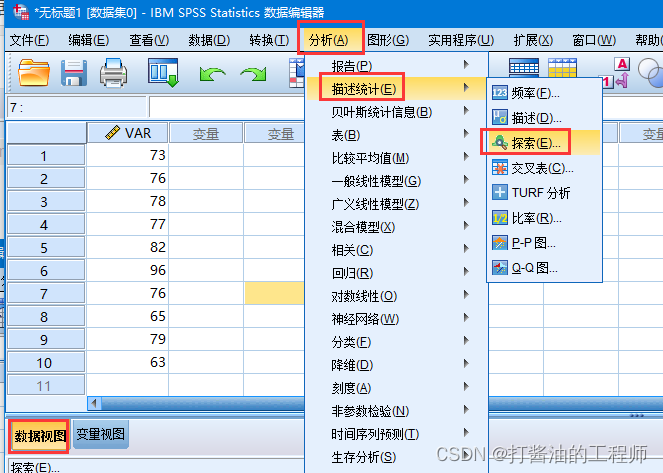
就会看到下述图片，将变量名加入因变量列表，点击图(T)…，我们可以选择输出图片（茎叶图、直方图），勾选含检验的正态图(O)。点击继续，如果想要输出图片，在输出应该选择两者都。选择确定。

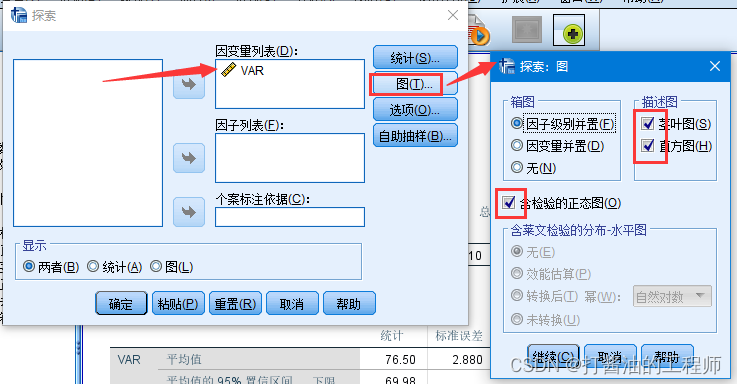
初始分析结果：

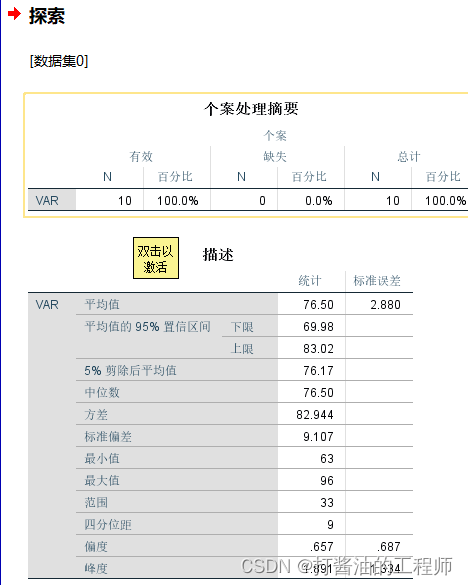
输出结果分析

探索描述，是对数据的统计总体描述。

两个重要统计量：偏度和峰度

描述标最下方的是：偏度和峰度。
偏度:
偏度（skewness）也称为偏态、偏态系数，是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。
详见：百度百科偏度-统计数据分布偏斜方向程度的度量。
峰度:
峰度（peakedness;kurtosis）又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来，峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量，如果峰度大于三，峰的形状比较尖，比正态分布峰要陡峭。反之亦然。
在统计学中，峰度（Kurtosis）衡量实数随机变量概率分布的峰态。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。
详见：百度百科峰度-衡量实数随机变量概率分布的峰态。
统计意义上：
引自：检验数据是否服从正态分布。

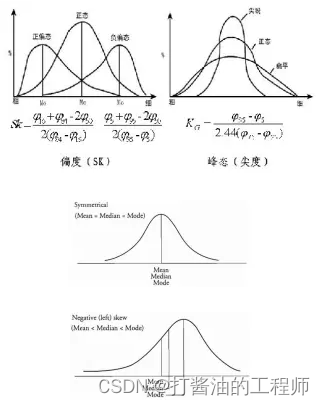
偏度SK越趋近0，数据越服从正态分布，众数=中位数=平均数；SK>0，为正偏态或左偏，众数<中位数<平均数；SK<0，为负偏态或右偏，众数>中位数>平均数。
峰度KG越趋近3，数据越服从正态分布；KG>3，峰度尖锐；KG<3，峰度扁平。（或exceess_KG=KG-3，exceess_KG越趋近0，数据越服从正态分布）。
但是仅根据偏度和峰度还不足以判断数据是否服从正态分布，需要做进一步的检验。

正态性检验结果

SPSS中检验数据是否呈“正态分布”主要通过Kolmogorov-Smirnova（K-S检验）和Shapiro-Wilk（S-W检验）。
当数据量50时，倾向以S-W检验结果为准；当数据量>50时，倾向以K-S检验结果为准；当数据量>5000时，SPSS则只会显示K-S检验结果。

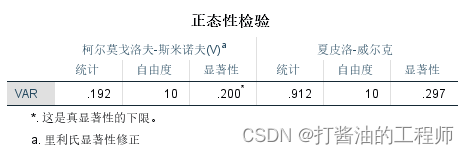
上表是生成的KS检验（D检验）和SW检验（W检验）的检验结果，此处我们关注的显著性是Sig.即P值。当P>0.05时，可以认为数据是呈正态分布的。
由上表可以看出，KS检验和SW检验显著性均>0.05。

其他图件输出

在输出结果部分还可以生成直方图、茎叶图、正态 Q-Q 图等，可以根据图形做出观测。
直方图：

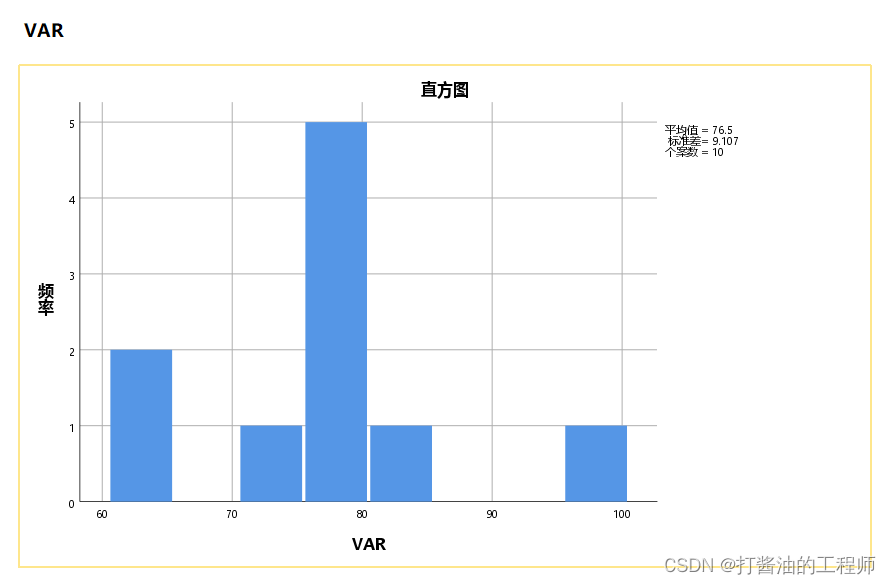
茎叶图：

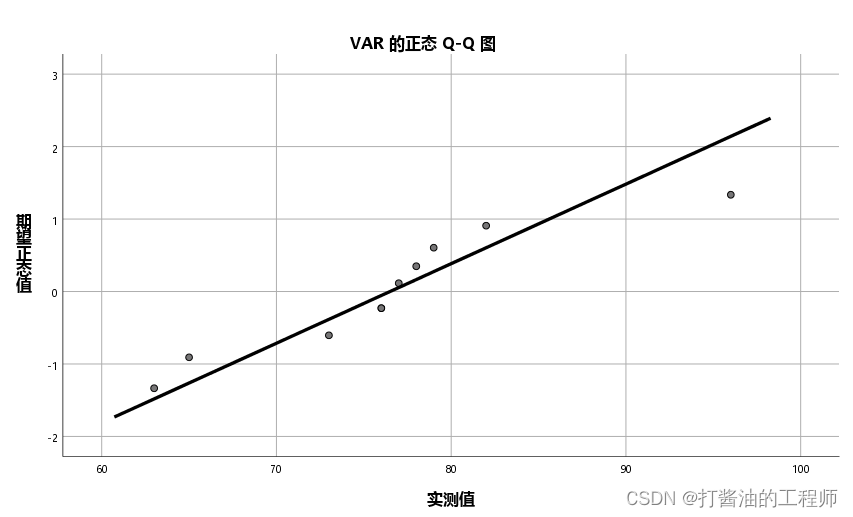
正态 Q-Q 图：

这篇关于SPSS|偏度和峰度|正态性分布检验|实战小练-SPSS学习（1）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---