Logistic Regression -- 单自变量

Why

传统的回归过程如线性回归解决的是$Y$为连续实数的情况。Logistic 回归是解决离散的分类问题，换句话说，要求$Y$是0或者1。
名字来自于指数分布家族中的Logistic 分布。

What

我们处理的是0-1分类问题. 输入n个样本, 第$i$个样本为$X_i, Y_i$. $X_i$是有限的离散空间, $Y_i$是$0$或$1$. 当$X= x_i$, $Y_i = 1$发生的概率为$P(Y_i = 1| X_i = x_i; \beta)$. 让$p_i= P(Y_i = 1| X_i = x_i; \beta)$, 则$1 - p_i = P(Y_i = 0| X_i = x_i; \beta)$ 且$\pi(x_i) = E(Y_i|X_i; \beta) = p_i = F(z_i)$. $z_i$是以$\beta$为参数的有关$X_i$的函数. 我们知道这是伯努利分布$Y_i \sim B(1, p)$, $F(z_i) = p_i$是累计分布函数.
让它更具体一些, 设$p_i = P(Y_i = 1 | X_i = x_i; \beta) = \frac{e^z_i}{1 + e^z_i} = F(z_i)$。具体针对回归问题来说，假设model是最简单的对X线性的Logistic regression， 则$Y = 1$事件发生的概率/比例/proportion为 $p = P(Y = 1 | X = x; \beta) = \frac{e^z}{1 + e^z} \in [0,1] \rightarrow z = log(\frac{p}{1-p}) = \beta_0 + \beta_1x.$ $F(Z) = p$ 形状是从0到1的S型.
通过$p$寻找$z$的过程也叫做logit变换($logit(p) = ln\frac{p}{1 - p}$), 得出的$z = \beta_0 + \beta_1x$毫无疑问是一条直线。所以Logistic regression 用一条直线来拟合做过logit变换后的proportion。 得出直线后我们再带入$x_i$到$p$即可做prediction了. 我们再对输出$p_i$取一个阀值(e.g. 0.5), 当$p \leq 0.5$时$Y_i$是0, 反之为1.

注: 其实不局限于用直线做拟合`, 只要是linear in parameters 的linear regression即可.

How

例子

图中所示为某城市心脏病数据。

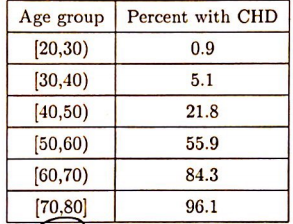
左手边列表示年龄段，右手边表对应年龄段中有心脏病的比例(占样本中的)。能看到随着年龄增长心脏病比例也相应增高.
设$\pi(X) = p$表年龄为$X$的人口中有心脏病的所占比例，取年龄段中点为该年龄段的代表年龄。以$\pi(X)$为数轴, $X$为横轴作图能看到呈S型(见下图), 因此我们可以考虑用Logistic Regression做拟合, 即用直线$\beta_0 + \beta_1 X$对做了Logit变换后的$\pi'(X)$建模. 这种模型叫做”Logistic Linear Model”.

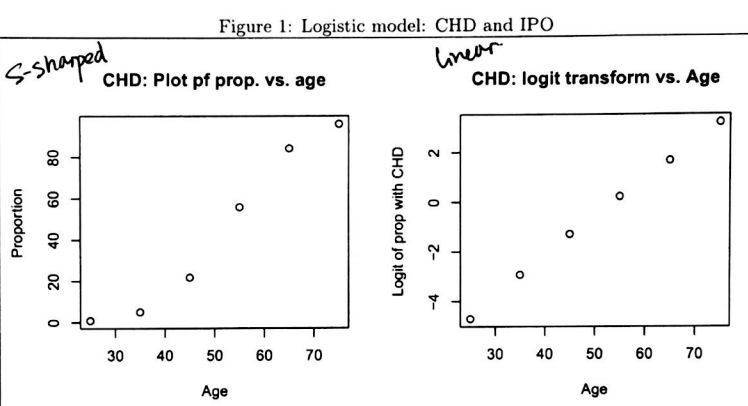
当我们找出合适的直线后, 对要预测的$X$带入$\pi(X) = exp(\beta_0 + \beta_1 X)/[1 + exp( \beta_0 + \beta_1 X)]$即是我们想要的预测值.

比如我们算得 β0≈−8.467,β