本文主要是介绍论文阅读笔记《Transductive Episodic-Wise Adaptive Metric for Few-Shot Learning》,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
小样本学习&元学习经典论文整理||持续更新
核心思想
本文提出了一种基于度量学习的小样本学习算法(TEAM),与其他基于度量学习的算法相比,本文在特征提取阶段采用了一种Task Internal Mixing (TIM)数据增强方法,设计了一种能够根据每个Episode进行自适应调整的距离度量方法Episodic-wise Adaptive Metric(EAM),并采用了一种双向相似性度量方法(Bi-SIM)来计算分类概率。算法的处理过程如下图所示
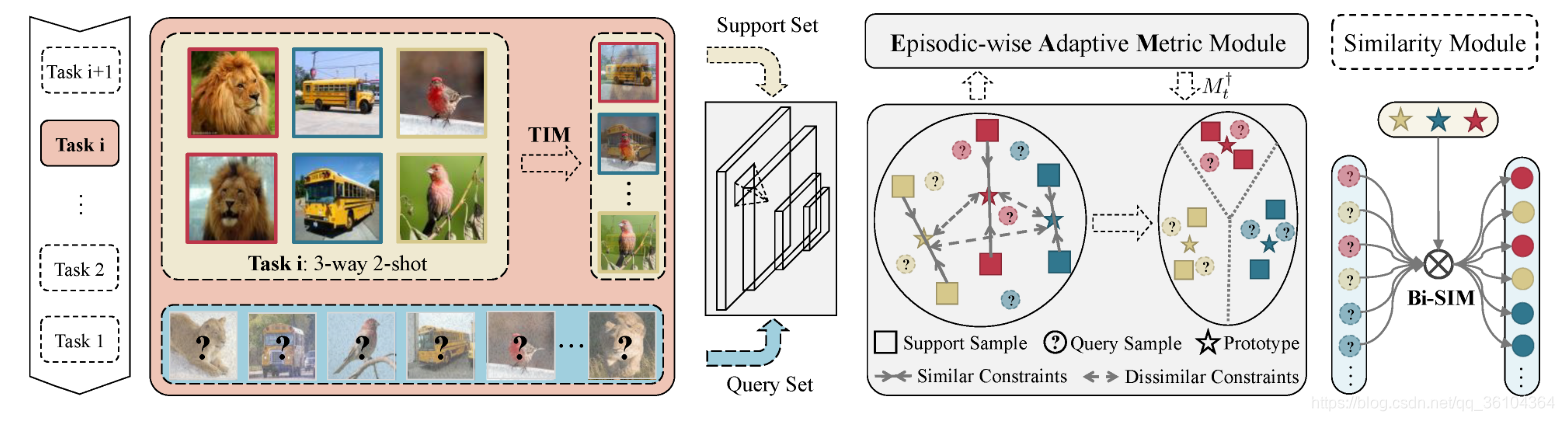
首先在特征提取阶段采用了TIM的数据增强方法来扩充数据集,对于每个任务中的两个样本 x i x_i xi和 x j x_j xj,按照如下的方式进行融合

式中 ω \omega ω是从[0.5,1.0]中随机采样得到的。本质上,TIM加入了一个先验,即如果两个样本在原始像素空间中相似,那么它们在特征空间中可能更接近。特征提取网络 f θ f_{\theta} fθ采用如下损失函数进行训练

式中 M T i M_{\mathcal{T}_i} MTi就是下面将要介绍的根据Episode进行自适应调整的距离度量方法。
然后,作者设计了EAM距离度量方法,给定两个特征向量 x i x_i xi和 x j x_j xj则二者之间的距离可以定义为下式

式中矩阵 M t M_t Mt参数化了向量空间中的一种马氏距离,例如当 M t M_t Mt为单位矩阵是,上式就表示欧氏距离。作者的想法就是通过优化的方式,对每个Episode都寻找到一个最优的 M t M_t Mt,使得相似的样本之间距离更小,不相似的样本之间距离更大,为了实现这个目标,作者提出以下优化问题

式中 M \mathcal{M} M表示相似样本的集合, C \mathcal{C} C表示不相似样本的集合,如何构建这两个集合后面会有介绍。利用拉格朗日乘子法可将上式转化为

式中

与PN算法相类似,类别 C C C对应的支持集 S C S_C SC,其类别原型 p c p_c pc为

则相似样本集 M \mathcal{M} M由三类样本构成:第一类 x i x_i xi和 x j x_j xj属于同一支持集, { x i ∈ S C , x j ∈ S C , i ≠ j } \left \{x_i\in S_C, x_j\in S_C, i\neq j\right \} {xi∈SC,xj∈SC,i=j};第二类 x i x_i xi属于 S C S_C SC,而 x j x_j xj属于该类对应的原型向量, { x i ∈ S C , x j ∈ P C } \left \{x_i\in S_C, x_j\in P_C\right \} {xi∈SC,xj∈PC};第三类 x j x_j xj是查询集 Q Q Q中 x i x_i xi的 k k k个最近邻, { x i ∈ S C , x j ∈ N ( x i , k , Q ) j } \left \{x_i\in S_C, x_j\in N(x_i,k,Q)j\right \} {xi∈SC,xj∈N(xi,k,Q)j}。
不相似样本集 C \mathcal{C} C由两类样本构成:第一类 x i x_i xi和 x j x_j xj属于不同的原型向量集, { x i ∈ P C , x j ∈ P C ′ , C ≠ C ′ } \left \{x_i\in P_C, x_j\in P_{C'}, C\neq C'\right \} {xi∈PC,xj∈PC′,C=C′};第二类 x j x_j xj属于训练集中的类别 C t r a i n C_{train} Ctrain对应的原型向量 P T P_T PT, { x i ∈ P C , x j ∈ P T } \left \{x_i\in P_C, x_j\in P_{T}\right \} {xi∈PC,xj∈PT}。
为了寻找到最优的 M t M_t Mt,需要对 d × d d\times d d×d个参数进行优化( d d d表示特征向量的维度),而对于一个Episode而言,其中所有的样本组合可能也不够 d × d d\times d d×d个,因此得到的模型就很容易过拟合。为了解决这个问题,作者引入了新的正则化约束

M 0 M_0 M0是一个与小样本任务先验有关的矩阵,上式本质上是约束了由 M t M_t Mt和 M 0 M_0 M0描述的两个混合高斯分布之间的KL散度。综上可以得到 M t M_t Mt的优化目标函数

但是如果采用SGD或其他的凸优化方法来求解上式计算复杂度将相当大,毕竟对于每个Episode都要计算一次,因此作者引入一种新的计算方法

M t ∗ M_t^* Mt∗表示最优解,为了进一步引入特征相关性信息,作者又在上式基础上增加了任务协方差矩阵 Σ t \Sigma_t Σt

则最终的EAM距离度量矩阵为

最后,本文又提出一种双向相似性度量方法(Bi-SIM)来计算分类概率,正常的概率计算方法都是利用Softmax函数计算查询样本 x i x_i xi属于类别 c c c的概率 s i → c s_{i\rightarrow c} si→c

而作者指出还应该计算原型向量 p c p_c pc属于查询样本 x i x_i xi的概率

最终的分类概率为二者的乘积

作者指出该策略能够有效地提高相似性度量方法的鲁棒性。可以看到上面的EAM计算和Bi-SIM计算过程中都用到了查询集中的样本,因此本文也属于直推学习(Transductive)类型。
实现过程
网络结构
特征提取的主干网络可以采用4-Conv或ResNet-18
创新点
- 在特征提取网络中引入TIM数据增强方法
- 设计了EAM距离度量函数,根据每个Episode寻找最佳的距离度量函数
- 设计了Bi-SIM双向相似性度量方法,用于分类概率计算
算法评价
本文引入和设计了非常多新的概念和方法,尤其是核心内容EAM度量方法的设计部分,涉及到了半正定规划(SDP),优化理论,信息论和正则化约束中的许多概念,看起来还是很复杂的。但就实验结果来看,本文在多个数据集上的效果与同时期的基于度量学习的方法相比都没有明显的优势,只是在CUB-200数据集上取得了不错的效果。一顿操作猛如虎,但效果也就一般。
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。
这篇关于论文阅读笔记《Transductive Episodic-Wise Adaptive Metric for Few-Shot Learning》的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







