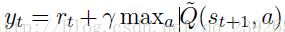本文主要是介绍NEC:Neural Episodic Control 阅读,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
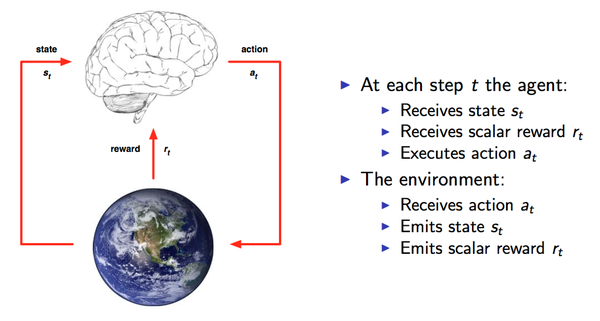
本文是google的DeepMind团队发布在arXiv上的文章,翻译过来是神经情景控制,相比于深度强化学习,可显著提高学习速度。
阅读本文需要了解的一些知识:
0 Abstract
1 Introduction
- 1.SGD优化需要较低的学习率。由于神经网络的全局近似性质,高学习率导致灾难性干扰。而低学习率意味着经验只能慢慢进入神经网络。
- 2.对于一个神经网络那些具有稀疏反馈(reward)信号的环境很难被建模,因为可能只有非常少的情况下reward 不为0。这可以被看作是一种类型不平衡的形式,低反馈样本超过未知数量的高反馈样本。 因此,神经网络在预测较大的反馈方面不成比例地表现不佳,使得agent难以选择reward 最高的行为。
- 3.通过value-bootstrapping技术,反馈信号传播,如Q-learning,导致经过先前与环境交互的历史,反馈信息一次只传播一步。如果变化出现时更新以相反的方向发生,那么这可能非常有效。然而为了训练不相关的小批量DQN-style,算法在随机选择的变化(transition)上训练,并且为了进一步稳定训练,需要使用缓慢更新的目标网络进一步减缓reward 传播。
2 Deep Reinforcement Learning


在DQN中,动作值函数Q(st,at)由卷积神经网络(CNN)参数化,卷积神经网络将状态st的2D像素表示作为输入,并输出包含该状态下每个动作的值的向量。当agent观察到变化,DQN存储(st, at,rt,st+1)元组到一个replay buffer(重放缓存),这部分内容将用于之后的训练。这个神经网络通过最小化该网络的输出(为Q(st, at))与Q-learning的目标输出yt的平方误差来进行训练。
其中,
即L(w)=E[(r+γmaxQ(s′,a′,w)−Q(s,a,w))2]
3 Neural Episodic Control
- 处理像素图像的卷积神经网络
- 一组内存模块(每个action一个)
- 一个最终的网络,用来从actions内存中读出数据到Q(s,a)价值函数中。
3.1 Differentiable Neural Dictionary (DND)
每个action都有一个简单的 内存模块Ma=(Ka,Va),其中Ka,Va是动态大小的向量阵列,每个都包含相同数量的向量。存储器模块用作从键到对应值的任意关联,非常类似于程序中的字典数据类型。 因此,我们将这种内存模块称为可微分神经字典(DND)。在DND上有两种操作:查询和写入,如图1所述。在DND上执行查找将键h映射到输出值
o:o=∑ wi vi (1)
其中vi是Va中的第i个元素,
wi =k(h,hi)/∑_j k(h,hj )(2)
其中hi是Ka的第i个元素,k(x,y)是一个核函数,eg:高斯函数或者反向核函数。因此,DND中的查找的输出是存储器中的值的加权和,其权重由查询键和存储器中的相应键之间的归一化内核给出。 为了能够在非常大的存储模块中高效的进行查询,我们将在实践中做出两个近似:首先,我们应该限制(1)到p最近邻(p=50)范围内。其次,我们使用近似最近邻近算法来执行基于kd-tree的查找(Bentley)。
查询DND后,会将新的键值对写入内存。写入的关键字对应于查找的关键字。 相对应的值是特定于应用程序的(下面我们指定NEC agent的更新)。 写入DND的过程是只在尾部追加的:通过分别将键和值附加到数组Ka和Va的末尾来写入存储器。 如果存储器中已经存在key,则其相应的值将被更新,而不是重复。
请注意,DND是Blundell等人描述的内存模块的可微分版本。 它也是对(Vinyals等人,2016; Kaiser等人,2016)中描述的用于分类的记忆和查找方案的概括。
/*为什么要用CNN处理输入s,然后输出一个向量h?
1.因为输入状态的可能性非常多,输出h相当于对输入s进行降维。
2.输出h是一个嵌入向量,可以计算h之间的距离来衡量这些h之间的相似度。*/
3.2 agent架构
图2显示了单个action的NEC agent的一部分的DND,而算法1描述了NEC算法的总体轮廓。像素状态s由卷积神经网络处理以产生key h。 然后,key h用于从DND查找值,处理存储器阵列的每个元素产生权重wi。 最后,输出DND中的value的加权和。(这一过程可描述为: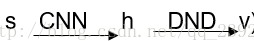
![]() )在NEC agent中,,DND中的值是对应于最初导致将对应的键值对写入存储器的状态的Q值。 因此,这种架构为单个给定动作a产生Q(s,a)的估计。该agent对每个action都有一个这样的架构(architecture),网络的卷积部分在每个单独的DND Ma之间共享参数。 NEC agent根据最高的Q值估计来决定在每一步中执行哪个action。(即在每一步中,针对每个action,在对应的DND中计算Q-value值(即(1)中得到的o值),执行最高的Q值对应的action)在实际中,训练时我们使用小ε值的ε-贪心策略。
)在NEC agent中,,DND中的值是对应于最初导致将对应的键值对写入存储器的状态的Q值。 因此,这种架构为单个给定动作a产生Q(s,a)的估计。该agent对每个action都有一个这样的架构(architecture),网络的卷积部分在每个单独的DND Ma之间共享参数。 NEC agent根据最高的Q值估计来决定在每一步中执行哪个action。(即在每一步中,针对每个action,在对应的DND中计算Q-value值(即(1)中得到的o值),执行最高的Q值对应的action)在实际中,训练时我们使用小ε值的ε-贪心策略。
![]()
![]()
![]()


图 1.DND上的操作图解。右边是查找操作,即根据CNN得到的h(蓝色竖长条)来计算得到一个o值。左边是写入操作,将h与查找得到的o值写入内存中。
![]()
![]()
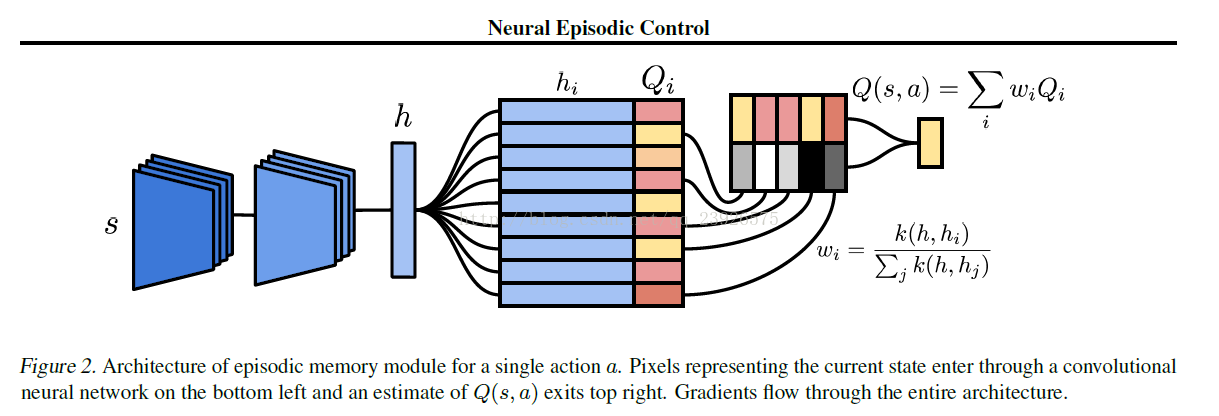
图 2.对单个动作 a 的情景记忆模块(episodic memory module)的架构。表示当前状态的像素进入通过左下方的一个卷积神经网络,然后在右上方输出 Q(s, a) 的一个估计。梯度会流过这整个架构。
3.3添加(s,a)键值对到内存
作为NEC agent,它不断地向其内存添加新的键值对。按照卷积神经网络编码得到的key h的值,键被附加到相应动作的存储器上。现在我们来看key对应的value的问题。在Blundell等人的文章中,蒙特卡罗(Monte Carlo)的返回值被写入内存。我们发现,蒙特卡罗回报(策略)和非策略性备份的混合效果更好,所以对于NEC,我们选择如Mnih等人在文章中使用的那样使用N阶Q-learning。这加入了以下N个策略回馈,并引导了trajectory(轨迹,可以理解为agent执行的一系列动作)剩余部分的折扣回馈和。 那么N阶Q值估计为:
![]()
max(Q(st+N,a)通过查询每个动作a的所有存储器Ma并获取返回的最高估计Q值。注意到,最早的可以添加到内存中的这样的值,是在特定(s,a)对发生之后的N步之后了。
/*上面这一段提到了on-policy和off-policy,这部分内容较多,由于时间问题,没来得及对这部分内容深入挖掘,有兴趣的可以查资料学习一下。公式(3)其实就是将2部分的提到的yt=rt部分内容进行了改进,即原来是只求执行当前action后到下一个状态能获得的最大反馈,现在修改为求执行当前action后到N步之后的状态所能获得的最大反馈。*/
当state-action value已经存在于DND中时(i.e key h已经存在于Ka中),对应的value:存于Va中的value和Qi-value,使用和Q-learning相同的算法进行更新:
![]()
![]()
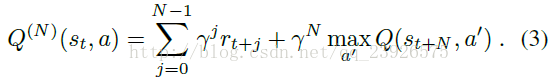
/*此处需要注意,根据DND求出的Q(s,a)和此处的Q(N)(st,a)是不同的,Q(s,a)只是为了求出在当前状态下执行每个动作能够得到的一个Q-value值,然后基于这些信息选出一个action 。执行action后环境会给出一个反馈reward,根据这歌反馈可以求出Q(N)(st,a)值。*/
其中,α是Q更新的学习率。如果state尚不存在,将Q(N)(st,a)加入Va中,将h加入到Ka中。我们发现α可以取一个高值,允许具有稳定表示的反复访问状态来快速更新其value 函数估计。此外,批量存储器更新(例如,在episode(情景)结束时)有助于提高计算性能。当我们达到内存的最大容量时,我们将覆盖最少的最近显示为邻居的item(这一句话目前还不太理解,猜测可能是指当memory module无法再添加新的键值对时,则根据当前的状态以及memory module 选择与当前状态最接近的且最少出现的item进行覆盖)。
3.4 Learning
Agent的参数通过最小化预测的Q value和Q(N)在从replay buffer上随机取样的小批量数据上的估计之间的L2损失来进行更新。特别地,我们存储元组(st,at,Rt)到replaybuffer,N是N-stepQ 规则的边界值,Rt=Q(N)(st,a)起到在DQN中见到的目标网络的作用(Rt也就是起到了2中DQN部分提到的yt的作用)。这些(st,at,Rt)元组随后经过随机采样得到minibatch以用于训练。注意到在图2中的架构是完全可微分的,因此我们可以通过梯度下降的方法来最小化L2损失。反向传播使用比在之前查询表后更新Q值使用的学习率α更小的学习率α,利用这个L2损失的梯度来更新卷积神经网络的权重和偏差(w和b)和每个特定action的内存里的key值和value值。
4 Experiment
这部分内容是实验部分,作者确定了NEC的一些参数,并将NEC与DQN、A3C、Q*(λ)、Retrace(λ)、Prooritised Replay、MFEC等方法在不同的Atari游戏上的性能进行了对比,比较了性能和学习效率,可以看到NEC的性能非常好,并且能够显著提升学习效率。这部分内容不再阐述,建议直接看原文就好。 5 Relate Work
略。
6 Discussion
我们已经提出了NEC:一个在Atari2600的游戏上相比其他agents学习效率显著提高的深度强化学习agent。NEC的核心是memory结构:一个可微分的神经词典(DND),每个潜在的action一个DND。 我们的实验表明,NEC与以前提出的数据效率要求相比,与环境的交互次数要少一个数量级。我们推测NEC通过结合以下三个特点使得NEC能够更快的学习:DND;N-stepQ估计;CNN提供的状态表示。 内存架构DND快速集成了最近的经验状态表示s和相应的价值估计value,可以将这些信息快速集成到未来的行为中。这样的Memories在许多情景中持续存在,我们使用快速的近似最近邻算法(kd-tree)来确保可以高效地访问这些存储器。通过使用N阶 Q值函数来估计Q值在蒙特卡罗value估计和非策略估计之间插值。蒙特卡罗value估计反映了agent实际收到的反馈,非策略估计应该更能代表最优策略的value 函数,但速度要慢得多。通过综合使用这两个估计,NEC可以在这两个估计程序之间进行权衡以及他们的相对优势和劣势(反馈传播速度与最优性能)。最后,通过卷积神经网络提供的缓慢变化的稳定表示,存储在DND中的keys保持相对稳定。我们的工作表明,非参数化方法对于深层加强学习工具来说是一个有希望的补充,特别是在数据效率至关重要的地方。在我们的实验中,我们看到在开始学习的过程中,NEC在学习速度方面优于其他agent。 我们看到,稍后的学习过程中Prooritised Replay的性能要高于NEC。 我们将其纳入未来的工作,以进一步改善NEC,使其长期的最终表现显著优于参数代理。 进一步研究的另一个途径是将本文讨论的方法应用于更广泛的任务,如视觉更复杂的3D世界或现实世界任务,其中数据效率非常重要,因为获取数据的消耗很高 。 ****************************************************************************************************************************************
本博客参考资料:
- 1.DeepMind论文:Neural Episodic Network
- 2. Deep Reinforcement Learning基础知识(DQN方面)
- 3.知乎专栏:智能单元DQN从入门到放弃系列
- 4. 一个 Q-learning 算法的简明教程
3.1 Differentiable Neural Dictionary (DND)
每个action都有一个简单的 内存模块Ma=(Ka,Va),其中Ka,Va是动态大小的向量阵列,每个都包含相同数量的向量。存储器模块用作从键到对应值的任意关联,非常类似于程序中的字典数据类型。 因此,我们将这种内存模块称为可微分神经字典(DND)。在DND上有两种操作:查询和写入,如图1所述。在DND上执行查找将键h映射到输出值
o:o=∑ wi vi (1)
其中vi是Va中的第i个元素,
wi =k(h,hi)/∑_j k(h,hj )(2)
其中hi是Ka的第i个元素,k(x,y)是一个核函数,eg:高斯函数或者反向核函数。因此,DND中的查找的输出是存储器中的值的加权和,其权重由查询键和存储器中的相应键之间的归一化内核给出。 为了能够在非常大的存储模块中高效的进行查询,我们将在实践中做出两个近似:首先,我们应该限制(1)到p最近邻(p=50)范围内。其次,我们使用近似最近邻近算法来执行基于kd-tree的查找(Bentley)。
查询DND后,会将新的键值对写入内存。写入的关键字对应于查找的关键字。 相对应的值是特定于应用程序的(下面我们指定NEC agent的更新)。 写入DND的过程是只在尾部追加的:通过分别将键和值附加到数组Ka和Va的末尾来写入存储器。 如果存储器中已经存在key,则其相应的值将被更新,而不是重复。
请注意,DND是Blundell等人描述的内存模块的可微分版本。 它也是对(Vinyals等人,2016; Kaiser等人,2016)中描述的用于分类的记忆和查找方案的概括。
/*为什么要用CNN处理输入s,然后输出一个向量h?
1.因为输入状态的可能性非常多,输出h相当于对输入s进行降维。
2.输出h是一个嵌入向量,可以计算h之间的距离来衡量这些h之间的相似度。*/
3.2 agent架构
图2显示了单个action的NEC agent的一部分的DND,而算法1描述了NEC算法的总体轮廓。像素状态s由卷积神经网络处理以产生key h。 然后,key h用于从DND查找值,处理存储器阵列的每个元素产生权重wi。 最后,输出DND中的value的加权和。(这一过程可描述为:)在NEC agent中,,DND中的值是对应于最初导致将对应的键值对写入存储器的状态的Q值。 因此,这种架构为单个给定动作a产生Q(s,a)的估计。该agent对每个action都有一个这样的架构(architecture),网络的卷积部分在每个单独的DND Ma之间共享参数。 NEC agent根据最高的Q值估计来决定在每一步中执行哪个action。(即在每一步中,针对每个action,在对应的DND中计算Q-value值(即(1)中得到的o值),执行最高的Q值对应的action)在实际中,训练时我们使用小ε值的ε-贪心策略。

图 1.DND上的操作图解。右边是查找操作,即根据CNN得到的h(蓝色竖长条)来计算得到一个o值。左边是写入操作,将h与查找得到的o值写入内存中。
图 2.对单个动作 a 的情景记忆模块(episodic memory module)的架构。表示当前状态的像素进入通过左下方的一个卷积神经网络,然后在右上方输出 Q(s, a) 的一个估计。梯度会流过这整个架构。
3.3添加(s,a)键值对到内存
作为NEC agent,它不断地向其内存添加新的键值对。按照卷积神经网络编码得到的key h的值,键被附加到相应动作的存储器上。现在我们来看key对应的value的问题。在Blundell等人的文章中,蒙特卡罗(Monte Carlo)的返回值被写入内存。我们发现,蒙特卡罗回报(策略)和非策略性备份的混合效果更好,所以对于NEC,我们选择如Mnih等人在文章中使用的那样使用N阶Q-learning。这加入了以下N个策略回馈,并引导了trajectory(轨迹,可以理解为agent执行的一系列动作)剩余部分的折扣回馈和。 那么N阶Q值估计为:
max(Q(st+N,a)通过查询每个动作a的所有存储器Ma并获取返回的最高估计Q值。注意到,最早的可以添加到内存中的这样的值,是在特定(s,a)对发生之后的N步之后了。
/*上面这一段提到了on-policy和off-policy,这部分内容较多,由于时间问题,没来得及对这部分内容深入挖掘,有兴趣的可以查资料学习一下。公式(3)其实就是将2部分的提到的yt=rt部分内容进行了改进,即原来是只求执行当前action后到下一个状态能获得的最大反馈,现在修改为求执行当前action后到N步之后的状态所能获得的最大反馈。*/
当state-action value已经存在于DND中时(i.e key h已经存在于Ka中),对应的value:存于Va中的value和Qi-value,使用和Q-learning相同的算法进行更新:
/*此处需要注意,根据DND求出的Q(s,a)和此处的Q(N)(st,a)是不同的,Q(s,a)只是为了求出在当前状态下执行每个动作能够得到的一个Q-value值,然后基于这些信息选出一个action 。执行action后环境会给出一个反馈reward,根据这歌反馈可以求出Q(N)(st,a)值。*/
其中,α是Q更新的学习率。如果state尚不存在,将Q(N)(st,a)加入Va中,将h加入到Ka中。我们发现α可以取一个高值,允许具有稳定表示的反复访问状态来快速更新其value 函数估计。此外,批量存储器更新(例如,在episode(情景)结束时)有助于提高计算性能。当我们达到内存的最大容量时,我们将覆盖最少的最近显示为邻居的item(这一句话目前还不太理解,猜测可能是指当memory module无法再添加新的键值对时,则根据当前的状态以及memory module 选择与当前状态最接近的且最少出现的item进行覆盖)。
3.4 Learning
Agent的参数通过最小化预测的Q value和Q(N)在从replay buffer上随机取样的小批量数据上的估计之间的L2损失来进行更新。特别地,我们存储元组(st,at,Rt)到replaybuffer,N是N-stepQ 规则的边界值,Rt=Q(N)(st,a)起到在DQN中见到的目标网络的作用(Rt也就是起到了2中DQN部分提到的yt的作用)。这些(st,at,Rt)元组随后经过随机采样得到minibatch以用于训练。注意到在图2中的架构是完全可微分的,因此我们可以通过梯度下降的方法来最小化L2损失。反向传播使用比在之前查询表后更新Q值使用的学习率α更小的学习率α,利用这个L2损失的梯度来更新卷积神经网络的权重和偏差(w和b)和每个特定action的内存里的key值和value值。
4 Experiment
5 Relate Work
6 Discussion
****************************************************************************************************************************************
本博客参考资料:
- 1.DeepMind论文:Neural Episodic Network
- 2. Deep Reinforcement Learning基础知识(DQN方面)
- 3.知乎专栏:智能单元DQN从入门到放弃系列
- 4. 一个 Q-learning 算法的简明教程
这篇关于NEC:Neural Episodic Control 阅读的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!