Transductive Episodic-Wise Adaptive Metric for Few-Shot Learning 论文笔记

摘要

如何利用少量的数据学习到一个generalizable 的分类器目前仍旧是小样本学习的一个挑战，基于这个出发点，作者把元学习(meta-learning)和深度度量学习和归纳推理想结合，通过探索每个任务中成对约束和正则化，我们将适应过程明确地公式化为标准的半定规划问题。作者针对每个任务设计了一个情节性的(episodic-wise)度量矩阵来将通用的，任务不可知的编码空间转换到一个可判别性高的，基于特定任务的编码空间中，除此以外作者提出了一个基于attention的双向相似度计算策略以此捕获出更鲁棒的相似度关系。创新点总结如下：

• 一个任务无关的编码器将输入图片转换为一个共享的编码空间中。
• 一个基于任务的适应性度量矩阵来完成不同任务之间的编码迁移。
• 新颖的双向相似度读量策略。

方法详解

1、任务无关的编码器chen

作者首先使用了一个任务无关的编码器$f_{\theta }$，利用随机梯度下降法，对训练集中的每个任务进行训练，损失函数为：

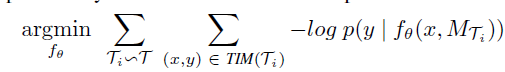
其中，$\tau$代指的为任务序列，$M_{{\tau }_i}$即为上文提到的基于任务的适应性度量矩阵。$TIM$为作者提出的任务间数据混合增强方法。具体详情如下：
对于来自两个任务的数据$(x_i,y_i)$，$(x_j,y_j)$作者同通过如下方式获取的新的数据$(\tilde{x},\tilde{y})$：

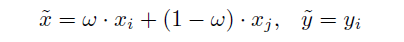
其中$1=>\omega >=0.5$，因此混合后的结果的label与 $x_i$保持一致。

2、episodic-wise 适应性度量方法

给定两个编码$x_i,x_j\in R^d$，作者通过如下方式来计算二者之间的距离：

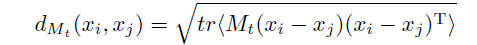
其中$M_t$是对马氏距离的一种参数化表示。作者首先 构造了成对约束损失函数，即最小化相同类别的距离，最大化不同类别的距离，具体的公式定义如下：

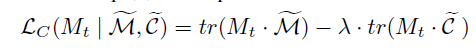
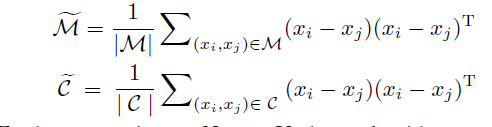
其中$\tilde{M}$代指的是同一类别的数据对集合，$\tilde{C}$代指的是不同类别之间的数据集集合，具体的构造方法为:

为了避免马氏距离的参数$M_t$过拟合，作者同时引入了正则项，即降低$M_t$和$M_0$之间的Bregman散度。其中$M_0$是从所有小样本任务中获取到的先验知识：

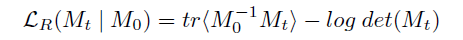
3、双向相似度度量

作者不仅仅是计算了query 集每个向量属于support集中 每个原型$p_c$的概率，同时计算了support 中每个原型属于每个 query 的概率。从而计算双向相似度来完成预测：

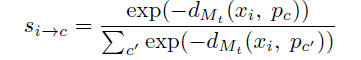
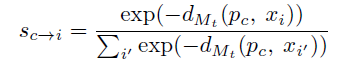
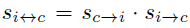
实验结果

作者在多个数据集上对方法进行了验证，具体结果如下：

miniImageNet

cifar-100

CUB