本文主要是介绍04工程训练:减振设计 2020-08-08,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、振动信号分析基础
信号分析系统的组成
数字信号采集
数字信号采集:采样
数字信号采集:量化
信号预处理:剔除异常点
信号预处理:去除均值和趋势项
信号预处理:重采样
二、背景介绍
振动的危害
机理与减振效果
三、振动机制
四、模态分析
有限元分析
求解过程
结果分析
避免共振
五、实验测量
实验装置
传感器固连方式
实验装置——数据采集系统
飞行试验
六、测量结果分析
幅值域分析
频域分析
时频域分析
七、隔振器设计
固有频率选择
隔振实验
八、数字滤波器设计
滤波器的概念
滤波器的选择
九、总结与未来展望
一、振动信号分析基础
信号分析系统的组成

数字信号采集
数字信号采集:将模拟信号转为数字信号的过程
- 模拟信号:时域和幅值域都连续的信号
- 数字信号:时域和幅值域都离散的信号
步骤:
- 采样(时域上的离散)
- 量化(幅值域上的离散)
数字信号采集:采样
采样:将模拟信号在指定时刻采集下来,并保持一段时间

参数:


采样定理:如果要从采样信号中完全重建原信号,则采集频率fs至少为原信号截止频率fc的两倍,即
![]()
频率混叠:当采样频率不能满足采样定理要求时,将会发生原信号高频成分(f > fs/2)被折叠到低频成分上的现象。
能相互混淆的频率:
![]()

(1/100s)就是100Hz,要是采样频率时500Hz的时候,也就是说在1/100 s中可以采样得到5个点
比如说,你要是对一个最高频率为400Hz的信号进行采样,采样频率需要大于(400*2=)800Hz
抗混叠方法:
- 提高采样频率:将增大数据量,并降低频率分辨率
- 采用抗混叠滤波器:采用模拟低通道滤波器将不感兴趣或不需要的高频成分滤掉
由于实际滤波器不是理想滤波器,因此 fs 取(2.5~5)fc
数字信号采集:量化
将采样点的信号与一组离散电平值进行比较,以最接近的电平值代替原信号,并变成有限长的二进制数字序列

(......这个在电子技术基础上有一些相似的见过的内容......)
信号预处理:剔除异常点
在数据测量、记录、传输等过程,因突然受严重噪声干扰、信号丢失、传感器失灵等因素,使记录信号引入一些异常的虚假值

偏离中心的异常值,不符合某些分布
信号预处理:去除均值和趋势项
趋势项:周期大于记录长度的频率成分
去除目的:避免后续处理出现过高的低频分量而溢出
去除步骤:
- 用最小二乘法对信号进行多项式拟合(还有其他的拟合方法)
- 减去拟合函数值

信号预处理:重采样

matlab里面有很多函数以及相关的文档
二、背景介绍
振动的危害
多旋翼飞行器振动的主要危害:
- 飞行板极易受振动信号的干扰,导致控制系统的反馈检测失真,极大影响飞行控制
- 降低多旋翼飞行器的振动具有很高的工程意义

机理与减振效果

三、振动机制
| 激励 | 系统存在两大类激励 1.周期性气动力(升力波) 2.电机与螺旋桨的动不平衡 |
| 系统 | 对多旋翼系统做出两个前提假设: 1.个向同性的线弹性体 2.将机臂视为欧拉伯努利梁 |
| 相应 |
|
四、模态分析
模态:机械结构的固有振动频率,每一个模态都有一个特定的固有频率、阻尼比和模态振型
模态分析:通过计算或实验的方法来获得这些模态参数的过程

有限元分析
- 有限元分析(FEA,Finite Element Analysis)利用有限数量的党员,去逼近无限未知量的真实系统,从而将偏微分(无限维)转换为常微分方程(有限维)
- 有限元模态分析:将一个弹性连续体的振动问题,离散为一个以有限个节点位移为广义坐标的多自由度系统的振动问题,再用模态叠加法求解
- 画网格
- 常用软件:ANSYS、ABAQUS、COMSOL
求解过程

结果分析

避免共振

五、实验测量
实验装置

传感器固连方式

实验装置——数据采集系统

飞行试验
(......)
六、测量结果分析
幅值域分析



频域分析

时频域分析

七、隔振器设计
隔振器:连接设备和基础的弹性元件与阻尼元件,用以减少和消除由设备传递到基础的振动力和由基础传递到设备的振动。
在本文问题中,基础时机架中部,设备时惯性测量单元。

固有频率选择

频率比(振动的频率/固有频率)因此希望振动频率工作在大于固有频率3、4倍的范围
但是固有频率不能选的太低,否则可能和运动信号的频率发生失真
主要是橡胶圈的材料参数,这里橡胶圈斜着放可以把竖、横方向的振动都消除掉
隔振实验

八、数字滤波器设计
滤波器的概念
模拟滤波器和数字滤波器
数字滤波器有4种:

数字滤波器尤有两种:
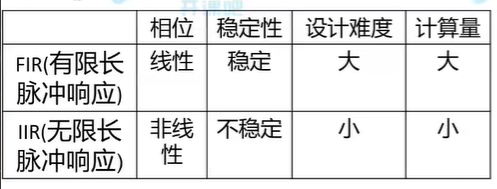
小型无人机常用低阶IIR低通滤波器(如二阶巴特沃斯低通滤波器)
滤波器的选择
低通滤波器的两个缺陷:
- 造成较大的相位滞后,这种滞后可能导致姿态控制超调甚至发散
- 由于真实的运动信号有非周期项,频域上会铺满整个频谱,低通滤波器的引入使得这部分信号失真
陷波器:二阶带阻滤波器,其设计简单程度和运算速度与二阶低通滤波器相当,适合工程应用。
然而由于陷波器只是二阶,能消除的频带过窄。带宽更宽的带阻滤波器可以达到更好的效果
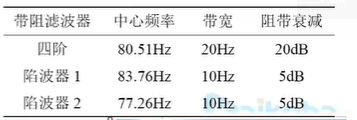


四阶的效果更好
九、总结与未来展望

这里是考虑相位的变化的影响,之前都是幅值和频率
这篇关于04工程训练:减振设计 2020-08-08的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









