SMOTE合成少数过采样技术

本文主要是介绍SMOTE合成少数过采样技术，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. SMOTE

JAIR’2002的文章《SMOTE: Synthetic Minority Over-sampling Technique》提出了一种过采样算法SMOTE。概括来说，本算法基于“插值”来为少数类合成新的样本。

设训练集的一个少数类的样本数为T，那么SMOTE 算法将为这少数类合成NT个新样本。
考虑少数类一个样本 i，特征向量 $x_i,i\in 1,...,T$:

1. 首先从该少数类的所有样本中找到 $x_i$ 的k 个近邻，如利用欧式距离，记为 x i ( n e a r ) , n e a r ∈ { 1 , . . . , k } x_{i (near)}, near \in\{1,...,k\} xi(near)​,near∈{1,...,k};
2. 从这k 个近邻中随机选择一个样本 $x_{i(nn)}$, 再生成一个 0~ 1之间的随机数${\zeta }_1$，
   从而生成一个新样本 $x_{i1}$.

${\mathbf{x}}_{i1}={\mathbf{x}}_i+{\zeta }_1\cdot \left({\mathbf{x}}_{i(nn)}-{\mathbf{x}}_i\right)$
3. 将步骤2重复 N 次，可以合成N个新样本；
4. 对全部的T 个少数类样本进行上述操作，可生成 NT 个新样本。

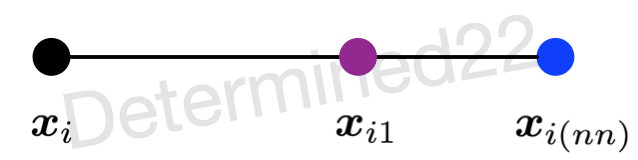
总的来说，SMOTE就是利用插值来合成样本，而且，添加了随机性，一方面是从 k 个近邻随机选择一个样本，另一方面是，产生 $\zeta$随机数。

---

参考:

1. cnblog 博客园机器学习 —— 类不平衡问题与SMOTE过采样算法

这篇关于SMOTE合成少数过采样技术的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---