GeoHash算法获取附近店铺和距离

本文主要是介绍GeoHash算法获取附近店铺和距离，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 简介

GeoHash算法将二维经纬度坐标直接转换成字符串，每一个字符串代表一个矩形区域，也就是说，这个矩形区域内所有的点（经纬度坐标）都共享相同的GeoHash字符串，字符串的长度越大，矩形的区域就越小，经度也就越高。字符串相似的表示距离相近，这样可以利用字符串的前缀匹配来查询附近的POI信息。

2. GeoHash算法

地球纬度区间是[-90,90]，经度区间是[-180,180]，通过区间法对经度和纬度分别进行计算，假如我们获取到的当前坐标为经度-0.12866, 纬度38.534413，以纬度为例：

• 将纬度平均分成两个区间：[-90,0),[0,90]，成为左区间和右区间，可以判断出38.534413属于右区间，则值为1,（如果属于左区间则值为0）；

• 接着将右区间继续划分，就变成了[0,45),[45,90],此时，38.534413属于左区间，则值为0

• 递归上述过程，则区间的值会越来越逼近38.534413

• 随着算法的进行，我们将会得到一个序列，序列的长度跟递归的次数有关，但是一定要保证的是经度和纬度的序列长度是一样的，我这里设置的递归长度是30，经度和纬度加起来就是60，

• 根据算法我们最终得到经度的序列为
  [0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0,0]，
  纬度的序列为
  [1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1,0]，然后我们根据此序列再组合一个新的序列偶数位放经度，奇数位放纬度，把2串编码组合生成新串[0, 1, 1, 0, 1, 1, 1, 1,1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0,0]，实际上这个序列是一串二进制

• 最后，我们将这个新串转换成十进制再使用0-9、b-z（去掉a, i, l, o）（base32编码）对这组十进制进行编码得到的字符串eyzgjnfr4p0p就是最终的GeoHash编码。

关于base32编码：

编码会去掉两种情况：
（1）元音，去除元音防止密码泄露，增加可靠性。如：hello world -> hll wrld
（2）容易混淆的字符，如：[1, I(大写i), l(小写L)]，[0,O]

Base32解码：

GeoHash算法利用Base32将全球划分成32个大的区域块。

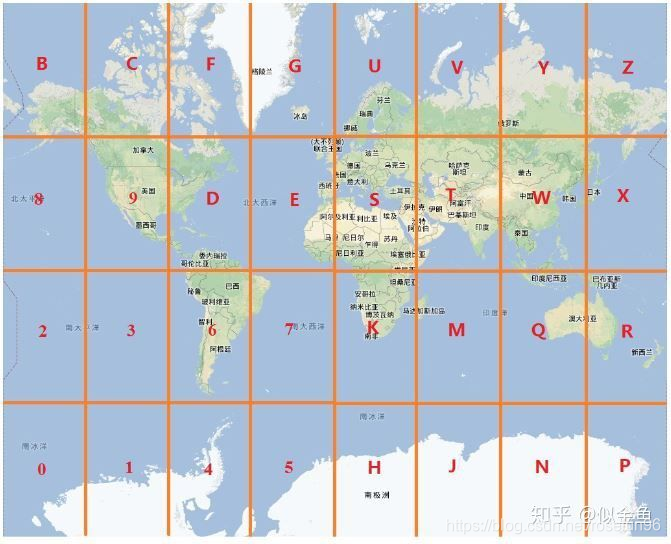
hash值转换成经纬度：


字符串越长，表示的范围越精确。5位的编码能表示10平方千米范围的矩形区域，而6位编码能表示更精细的区域（约0.34平方千米）。
a）在纬度相等的情况下：

经度每隔0.00001度，距离相差约1米；

每隔0.0001度，距离相差约10米；

每隔0.001度，距离相差约100米；

每隔0.01度，距离相差约1000米；

每隔0.1度，距离相差约10000米。

b）在经度相等的情况下：

纬度每隔0.00001度，距离相差约1.1米；

每隔0.0001度，距离相差约11米；

每隔0.001度，距离相差约111米；

每隔0.01度，距离相差约1113米；

每隔0.1度，距离相差约11132米。

其他base64编码.

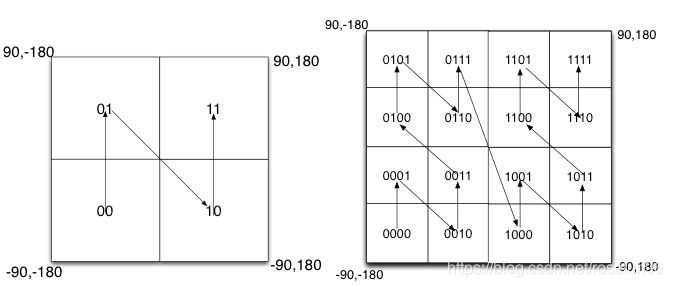
我们将二进制编码的结果填写到空间中，当将空间划分为四块时候，编码的顺序分别是左下角00，左上角01，右下脚10，右上角11，也就是类似于Z的曲线，当我们递归的将各个块分解成更小的子块时，编码的顺序是自相似的（分形），每一个子快也形成Z曲线，这种类型的曲线被称为Peano空间填充曲线。

这种类型的空间填充曲线的优点是将二维空间转换成一维曲线（事实上是分形维），对大部分而言，编码相似的距离也相近， 但Peano空间填充曲线最大的缺点就是突变性，有些编码相邻但距离却相差很远，比如0111与1000，编码是相邻的，但距离相差很大。

3. 查找topK近的店铺

在上图中查找A点附近的点时，由于A点和C点是在同一个区域内，根据GeoHash算法认为A点附近只有C点，没有B点。但是实际上B点离A点甚至要比C点还要近，为了取得更精确的结果，除了目标点的GeoHash值外，还需要使用A点周围8个区域值的GeoHash值。

---

参考：

1. base32;
2. Geohash;
3. GeoHash算法获取附近店铺和距离;
4. 作者：NilMe;
5. GeoHash核心原理解析;

这篇关于GeoHash算法获取附近店铺和距离的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---