本文主要是介绍SLAM从入门到精通(bresenham绘制算法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】
前面我们说过,学术界和工业界对于slam的要求是不一样的。前者要求robot在运动的过程中,同步实现定位和制图的操作。但是工业界中,一般两者是分开来的。首先进行制图,一旦制图完成之后就专注于定位操作。但是这两者之间没有明显的差别。
1、学术slam和工业slam的关系
整理来说,完全可以把工业界的应用看成是slam的一个特例。真正的slam一般是这样的,首先在robot开始的位置设置为原点,lidar扫描的地方,绘制出一个地图。接着,通过遥控按钮操作robot,这个时候robot就走到了一个新的位置。借助于odom数据、lidar数据和之前的地图数据,我们可以求解出robot新位置的坐标。这样,我们通过robot的新位置、lidar扫描数据,又可以绘制出新的地图了。循环往复,不断重复上面的过程,最终就会可以得到一个完整的地图。这就是slam的基本原理。
2、slam和定位的转换
有了上面的分析,大家也就明白了为什么很多论文都是讲slam算法,但是不谈具体的定位算法。这主要就是因为如果把slam算法中的制图删除、定位算法中的地图直接换成全局地图,这本身就是一个相对完整的定位算法方案了。
3、制图的算法
有了准确的位姿之后,制图就不复杂了。前面我们说过,制图其实就是绘制很多的射线。雷达无法扫描到的地方一般被认为是灰色。没有达到最远测量距离,提前返回来的地方,那就是黑色,也就是有障碍物的地方。而lidar和障碍物之间的区域,这就是白色,可以被认为是能够自由活动的区域。
上面这些描述,都是建立在lidar和base_link基本一致的基础上得出来的。如果两者不一致,那么还需要做一个tf转换。所以大家看到得是地图文件,实际上是通过一条、一条得射线绘制出来的。
4、bresenham算法
这个算法本身是属于计算机图形学的一个基本算法。我们平时在绘制直线的时候,很容易遇到浮点数。但是计算机屏幕上面是没有浮点数的,每一个x、y坐标都是一个整数。那么怎么把这些直线上的数据在屏幕上面显示出来,这就是bresenham算法所要解决的事情。
希望了解算法详细内容的同学,可以看下这个wiki连接,讲的还是很仔细的,
https://en.wikipedia.org/wiki/Bresenham%27s_line_algorithm5、编译和测试
不喜欢看算法,想直接看代码的同学也可以直接github上查找对应的代码。网上有很多bresenham算法的实现代码,这里给出一个链接,
https://gist.github.com/nowke/965fed0d5191bf373f1262be584207bb如果链接也不想看,这里给出一个可以编译版本的代码方案。主要是头文件需要修改下,
#include <GL/glut.h>
#include <stdio.h>int x1, y1, x2, y2;void myInit() {glClear(GL_COLOR_BUFFER_BIT);glClearColor(0.0, 0.0, 0.0, 1.0);glMatrixMode(GL_PROJECTION);gluOrtho2D(0, 500, 0, 500);
}void draw_pixel(int x, int y) {glBegin(GL_POINTS);glVertex2i(x, y);glEnd();
}void draw_line(int x1, int x2, int y1, int y2) {int dx, dy, i, e;int incx, incy, inc1, inc2;int x,y;dx = x2-x1;dy = y2-y1;if (dx < 0) dx = -dx;if (dy < 0) dy = -dy;incx = 1;if (x2 < x1) incx = -1;incy = 1;if (y2 < y1) incy = -1;x = x1; y = y1;if (dx > dy) {draw_pixel(x, y);e = 2 * dy-dx;inc1 = 2*(dy-dx);inc2 = 2*dy;for (i=0; i<dx; i++) {if (e >= 0) {y += incy;e += inc1;}elsee += inc2;x += incx;draw_pixel(x, y);}} else {draw_pixel(x, y);e = 2*dx-dy;inc1 = 2*(dx-dy);inc2 = 2*dx;for (i=0; i<dy; i++) {if (e >= 0) {x += incx;e += inc1;}elsee += inc2;y += incy;draw_pixel(x, y);}}
}void myDisplay() {draw_line(x1, x2, y1, y2);glFlush();
}void main(int argc, char **argv) {printf( "Enter (x1, y1, x2, y2)\n");scanf("%d %d %d %d", &x1, &y1, &x2, &y2);glutInit(&argc, argv);glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);glutInitWindowSize(500, 500);glutInitWindowPosition(0, 0);glutCreateWindow("Bresenham's Line Drawing");myInit();glutDisplayFunc(myDisplay);glutMainLoop();
}这里的编译命令是在ubuntu 20.04上实现的,如果有glut.h文件无法找到的错误,可以先安装一下这个库,
sudo apt-get install libglfw3-dev libgl1-mesa-dev libglu1-mesa-dev安装好库之后,就可以用命令gcc来编译了,
gcc draw.c -lglut -lGL -lGLEW -lGLU -o draw
一切顺利的话,就可以生成./draw文件。执行后,会看到一个提示,要求我们输入起点和终点的坐标,
feixiaoxing@feixiaoxing-VirtualBox:~/Desktop$ ./draw
Enter (x1, y1, x2, y2)
100 3 200 500
老老实实输入坐标后,按回车就可以看到对应的直线显示了,
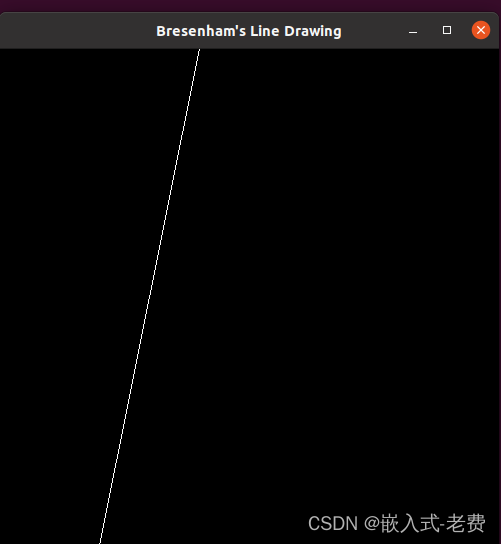
整个算法借助于opengl实现了显示过程。有兴趣的同学可以单步调试一下。
这篇关于SLAM从入门到精通(bresenham绘制算法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







