解读文献中的箱线图（Box-plot）和小提琴图（Violin-plot)）

关于文献中箱线图（Box-plot）和小提琴图（Violin-plot)）的解读

1、箱线图

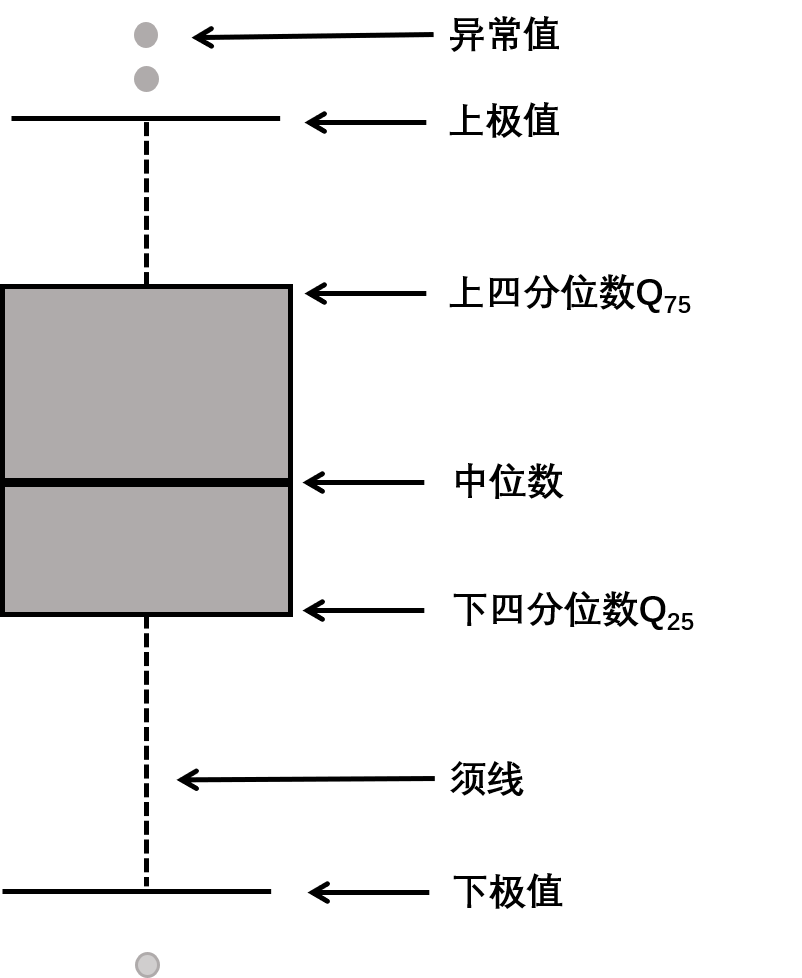
①箱子的大小取决于数据的四分位距（IQR），即Q75- Q25（Q75 ：75%分位数 , Q25: 25%分位数 , Q75和Q25为四分位数)。50%的数据集中于箱体，箱体大表示数据分布离散，数据波动较大，箱体小表示数据集中。

②箱子的上边为上四分位数Q75，下边为下四分位数Q25，箱体中的横线为中位数Q50（50%分位数）

③箱子的上触须为数据的最大值Max，下触须为数据的最小值Min（注意是非离群点的最大最小值）

④若数据值 > Q75+1.5 * IQR（上限值） 或 数据值 < Q25-1.5 * IQR（下限值） ,均视为异常值。数据值 > Q75+3 * IQR 或 数据值 < Q25-3 * IQR ,均视为极值。

⑤偏度：

对称分布：中位线在箱子中间

右偏分布：中位数更靠近下四分位数

左偏分布：中位数更靠近上四分位数

2、小提琴图

小提琴图 (Violin Plot)是用来展示多组数据的分布状态以及概率密度。这种图表结合了箱形图和密度图的特征，主要用来显示数据的分布形状。跟箱形图类似，但是在密度层面展示更好。在数据量非常大不方便一个一个展示的时候小提琴图特别适用。

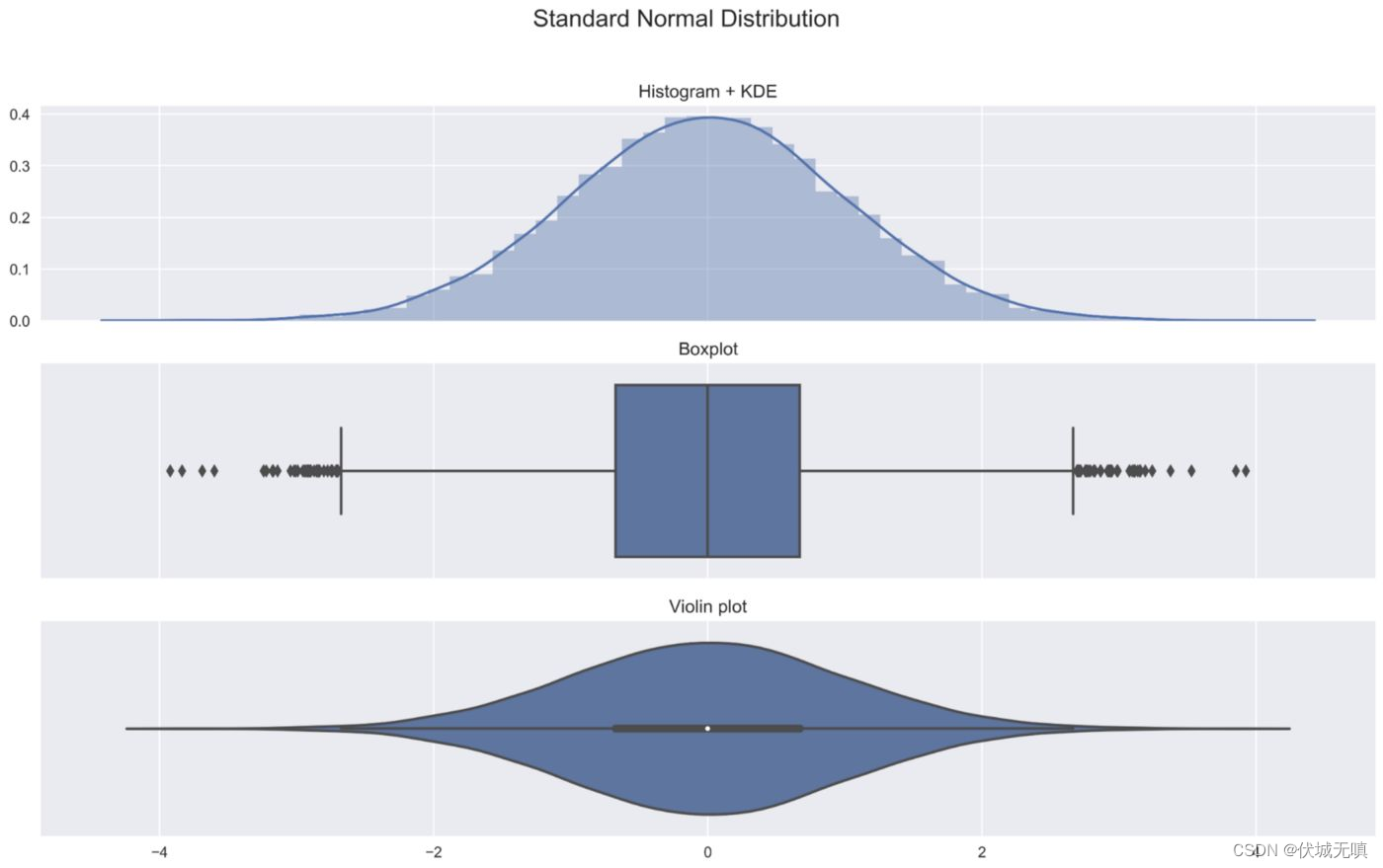
小提琴图的内部是箱线图（有的图中位数会用白点表示，但归根结底都是箱线图的变化）；外部包裹的就是核密度图，某区域图形面积越大，某个值附近分布的概率越大。用于创建小提琴图的核密度图与添加在直方图上的核密度图是一样的。

通过箱线图，可以查看有关数据的基本分布信息，例如中位数，平均值，四分位数，以及最大值和最小值，但不会显示数据在整个范围内的分布。如果数据的分布有多个峰值（也就是数据分布极其不均匀），那么箱线图就无法展现这一信息，这时候小提琴图的优势就展现出来了！
我相信，将这三张图放在一起展示，可以清晰的看到小提琴图什么样子以及它包含什么样的直觉信息。