本文主要是介绍第一门课:神经网络和深度学习(第三周)——浅层神经网络,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
浅层神经网络
- 1. 神经网络概览
- 2. 神经网络的表示
- 3. 神经网络的输出
- 4. 多样本向量化
- 5. 激活函数
- 6. 为什么需要非线性激活函数
- 7. 激活函数的导数
- 8.直观理解反向传播
- 9. 随机初始化
1. 神经网络概览

对于以往由逻辑单元组成的简单神经网络,我们对其计算过程已经大致了解。接下来我们类比于浅层神经网络中。
算法过渡:

逐步求解:

第一层根据输入计算 z [ 1 ] z^{[1]} z[1] ,然后计算第一层的输出 a [ 1 ] a^{[1]} a[1]。

把第一层的输出 a [ 1 ] a^{[1]} a[1] 作为第二层的输入, 计算 z [ 2 ] z^{[2]} z[2], 代入 sigmoid 函数, 得到输出 a [ 2 ] a^{[2]} a[2], 进而计算损失函数。

还有反向的求导过程。
2. 神经网络的表示

3. 神经网络的输出

每个神经网络单元的工作包括两部分:计算 z z z ,然后根据激活函数 (sigmoid) 计算 σ ( z ) \sigma(z) σ(z)
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) z 2 [ 1 ] = w 2 [ 1 ] T x + b 2 [ 1 ] , a 2 [ 1 ] = σ ( z 2 [ 1 ] ) z 3 [ 1 ] = w 3 [ 1 ] T x + b 3 [ 1 ] , a 3 [ 1 ] = σ ( z 3 [ 1 ] ) z 4 [ 1 ] = w 4 [ 1 ] T x + b 4 [ 1 ] , a 4 [ 1 ] = σ ( z 4 [ 1 ] ) \begin{array}{ll} z_{1}^{[1]}=w_{1}^{[1] T} x+b_{1}^{[1]}, & a_{1}^{[1]}=\sigma\left(z_{1}^{[1]}\right) \\ z_{2}^{[1]}=w_{2}^{[1] T} x+b_{2}^{[1]}, & a_{2}^{[1]}=\sigma\left(z_{2}^{[1]}\right) \\ z_{3}^{[1]}=w_{3}^{[1] T} x+b_{3}^{[1]}, & a_{3}^{[1]}=\sigma\left(z_{3}^{[1]}\right) \\ z_{4}^{[1]}=w_{4}^{[1] T} x+b_{4}^{[1]}, & a_{4}^{[1]}=\sigma\left(z_{4}^{[1]}\right) \end{array} z1[1]=w1[1]Tx+b1[1],z2[1]=w2[1]Tx+b2[1],z3[1]=w3[1]Tx+b3[1],z4[1]=w4[1]Tx+b4[1],a1[1]=σ(z1[1])a2[1]=σ(z2[1])a3[1]=σ(z3[1])a4[1]=σ(z4[1])
[ layer ] 上标表示第几层,下标表示该层的第几个节点。


输入一个样本的特征向量,四行代码计算出一个简单神经网络的输出,那么输入多个样本呢?请往下看。
4. 多样本向量化
-
对于 m \mathrm{m} m 个样本, ( i ) (\mathrm{i}) (i) 表示第 i \mathrm{i} i 个样本
z [ 1 ] ( i ) = W [ 1 ] ( i ) x ( i ) + b [ 1 ] ( i ) a [ 1 ] ( i ) = σ ( z [ 1 ] ( i ) ) z [ 2 ] ( i ) = W [ 2 ] ( i ) a [ 1 ] ( i ) + b [ 2 ] ( i ) a [ 2 ] ( i ) = σ ( z [ 2 ] ( i ) ) \begin{aligned} z^{[1](i)} &=W^{[1](i)} x^{(i)}+b^{[1](i)} \\ a^{[1](i)} &=\sigma\left(z^{[1](i)}\right) \\ z^{[2](i)} &=W^{[2](i)} a^{[1](i)}+b^{[2](i)} \\ a^{[2](i)} &=\sigma\left(z^{[2](i)}\right) \end{aligned} z[1](i)a[1](i)z[2](i)a[2](i)=W[1](i)x(i)+b[1](i)=σ(z[1](i))=W[2](i)a[1](i)+b[2](i)=σ(z[2](i)) -
为了向量化计算,进行堆叠

注意: -
列向看,对应于不同的特征,就是神经网络中的该层的各个节点;
-
行向看,对应于不同的训练样本。
5. 激活函数

tanh激活函数是 sigmoid的平移伸缩结果,其效果在所有场合都优于sigmoid,tanh几乎适合所有场合。例外是,二分类问题的输出层,想让结果介于 0,1之间,所以使用 sigmoid 激活函数。
tanh、 sigmoid两者的缺点:在特别大或者特别小 z z z 的情况下,导数的梯度或者函数的斜率会变得特别小,最后就会接近于0,导致降低梯度下降的速度。
激活函数的选择经验:
-
如果输出是0、1值(二分类问题),输出层选择sigmoid函数,其它所有单元都选择Relu函数;
-
sigmoid函数需要进行浮点四则运算,在实践中,使用ReLu激活函数学习的更快;
-
隐藏层通常会使用Relu激活函数。有时,也会使用tanh激活函数,但Relu的一个缺点是:当是负值的时候,导数等于0;
-
另一个版本的Relu被称为Leaky Relu,当是负值时,这个函数的值不等于0,而是轻微的倾斜,这个函数通常比Relu激活函数效果要好,尽管在实际中Leaky ReLu使用的并不多。
6. 为什么需要非线性激活函数
线性隐藏层一点用也没有,因为线性函数的组合本身就是线性函数,所以除非你引入非线性,否则你无法计算出更有趣的函数,即使网络层数再多也不行。
- 不能在隐藏层用线性激活函数,可以用ReLU、tanh、leaky ReLU或者其他的非线性激活函数;
- 唯一可以用线性激活函数的通常就是输出层;在隐藏层使用线性激活函数非常少见。
7. 激活函数的导数
-
sigmoid

-
tanh

-
ReLu (Rectified Linear Unit)

z = 0 z=0 z=0 时,可以让导数为 0,或者 1。 -
Leaky ReLU (Leaky Linear Unit)

z = 0 z=0 z=0 时,可以让导数为 0.01,或者 1。
8.直观理解反向传播
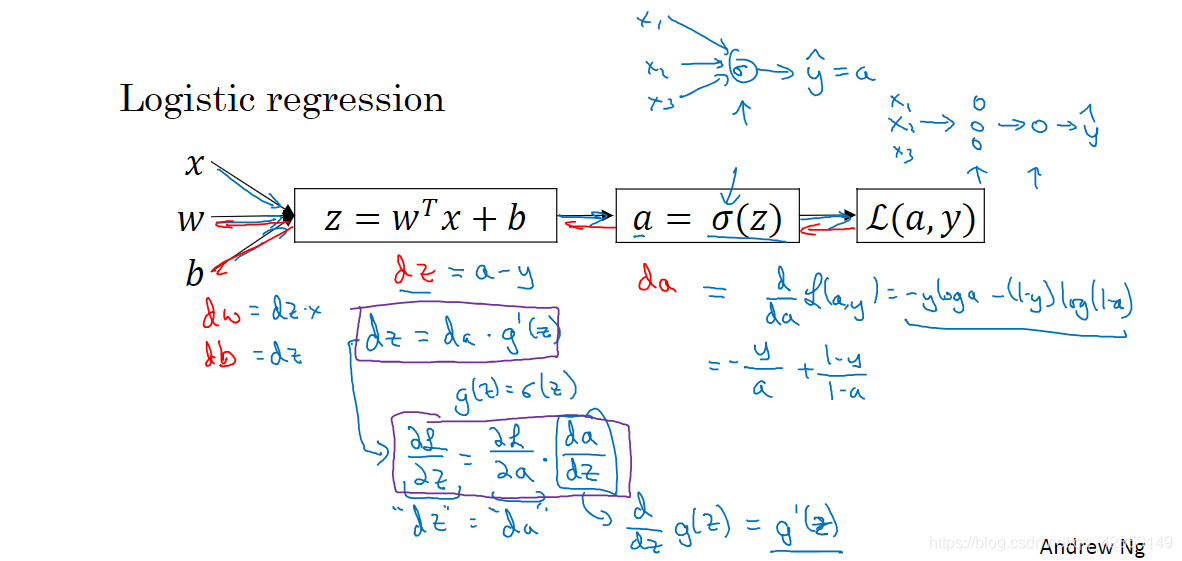
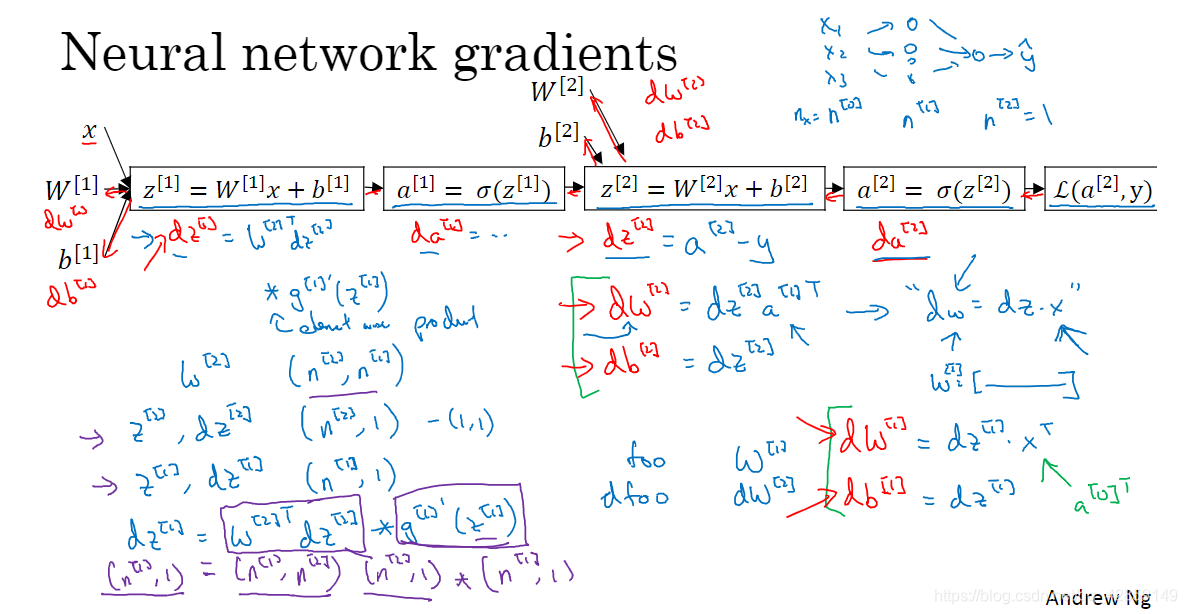

9. 随机初始化
对于一个神经网络,如果你把权重或者参数都初始化为0,那么梯度下降将不会起作用,并且会存在神经单元的对称性问题,添加再多的神经单元也没有更好的效果。

- 常数为什么是0.01,而不是100或者1000 ?因为如果w初始化很大的话,那么z就会很大,所以sigmoid/tanh 激活函数值就会趋向平坦的地方,而sigmoid/tanh 激活函数在很平坦的地方,学习非常慢。
- 当你训练一个非常非常深的神经网络,你可能要试试0.01以外的常数。
这篇关于第一门课:神经网络和深度学习(第三周)——浅层神经网络的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



