【计量经济学及Stata应用】第9章 模型设定于数据问题

9.1 遗漏变量

假设真实的模型（true model）：
$$y=\alpha +\beta x_1+\gamma x_2+\epsilon$$
实际估计模型（omitted model）：
$$y=\alpha +\beta x_1+\epsilon$$
对比两个方程可知，遗漏变量$x_2$被纳入新扰动项$u=\gamma x_2+\epsilon$

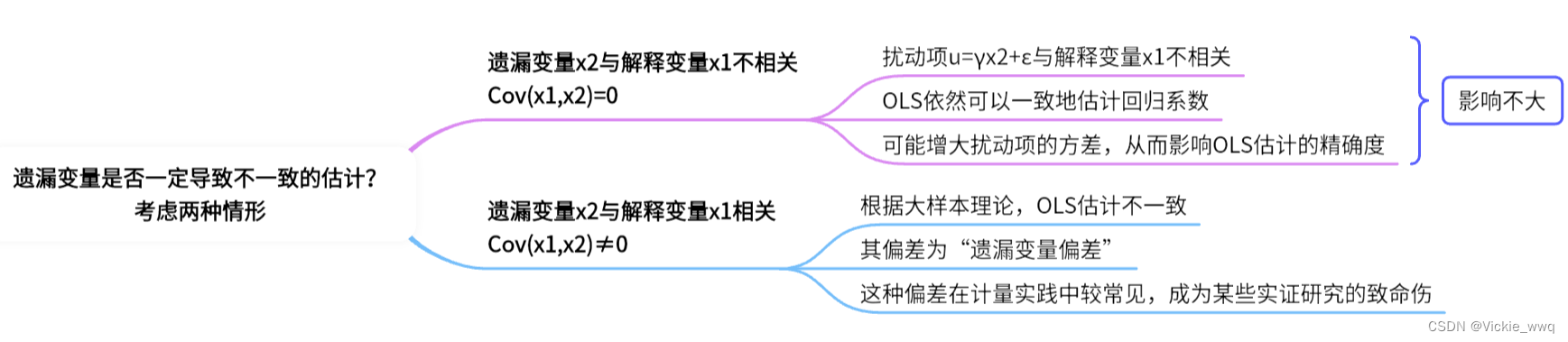
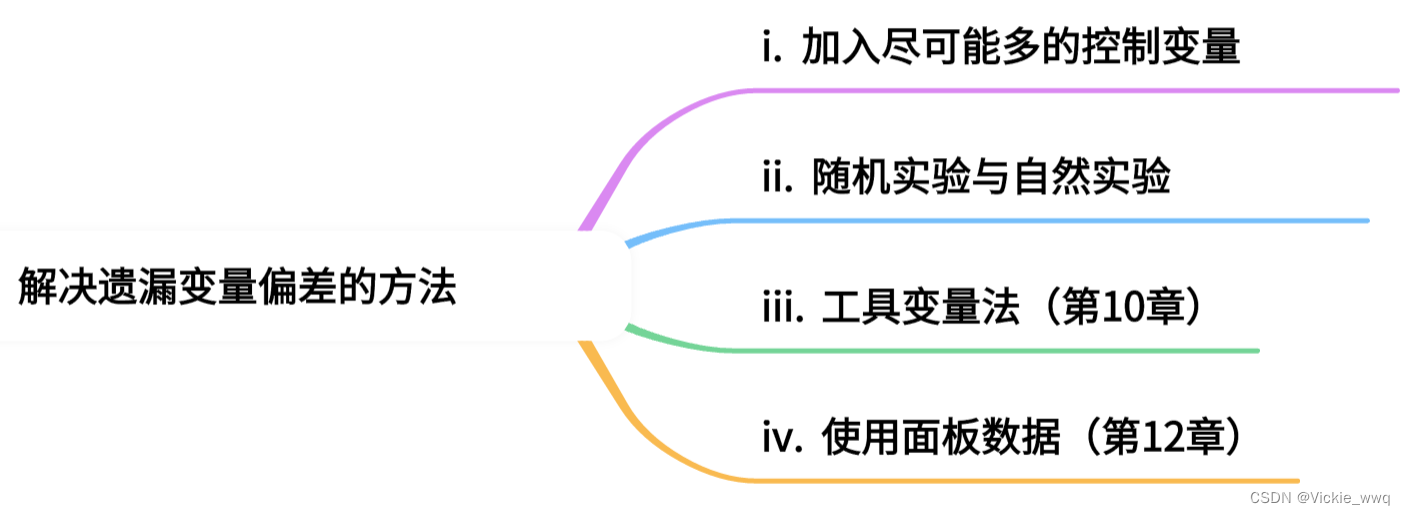
总之，由于影响被解释变量的因素往往很多，而局限于数据的可得性，故在任何实证研究中几乎总存在遗漏变量。因此，一篇专业水准的实证论文几乎总是需要说明，它是如何在存在遗漏变量的情况下避免遗漏变量偏差的。如果无法令人信服地说明这一点，则结果就是可疑的。

9.2 无关变量

假设真实的模型为：
$$y=\alpha +\beta x_1+\epsilon$$
其中，$Cov(x_1,\epsilon )=0$
实际估计的模型：
$$y=\alpha +\beta x_1+\gamma x_2+(\epsilon -\gamma x_2)$$
其中，加入了与被解释变量无关的解释变量$x_2$。由于真实参数$\gamma =0$，故可将模型写为：
$$y=\alpha +\beta x_1+\gamma x_2+\epsilon$$

OLS仍然一致。

然而，引入无关变量后，由于受到无关变量的干扰，估计量$\hat{\beta }$的方差一般会增大。总之，对于解释变量的选择最好遵循经济理论的知道。

9.3 建模策略：“由大到小”还是“由小到大”

9.4 解释变量个数的选择

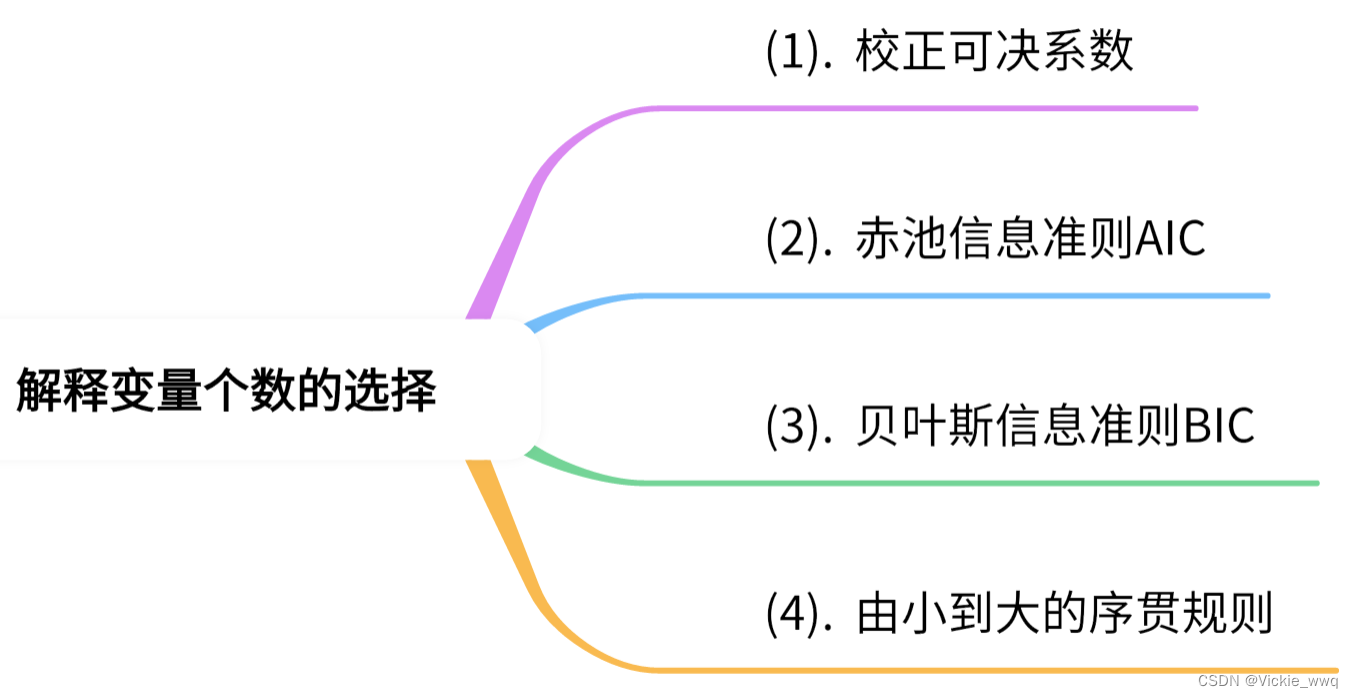
icecream.dta

//使用信息准则
quietly reg consumption temp price income
estat ic
quietly reg consumption temp L.temp price income	//加入一阶滞后项
estat ic
quietly reg consumption temp L.temp L2.temp price income	//加入二阶滞后项
estat ic//使用序贯t规则
reg consumption temp L.temp L2.temp price income	//假设pmax=2
reg consumption temp L.temp price income	//pmax-1

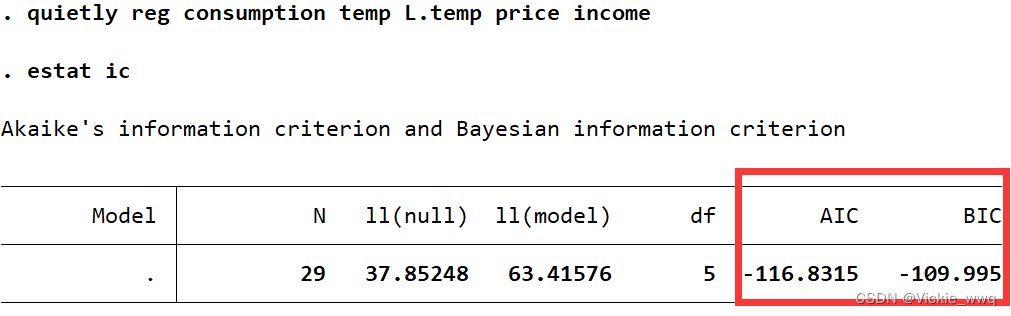
加入一阶滞后项后，AIC和BIC都下降了


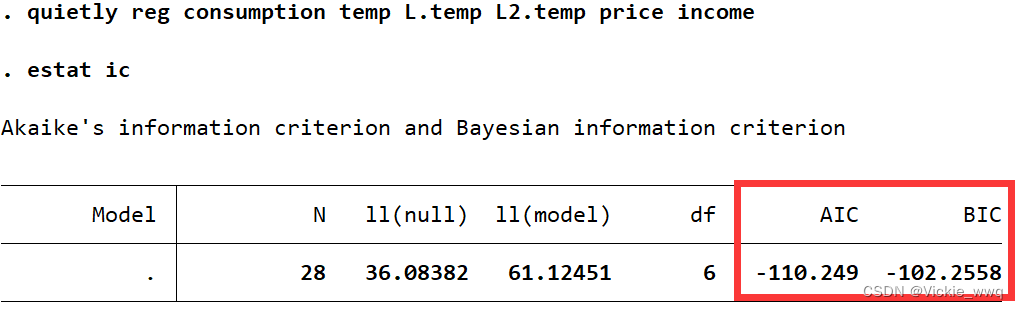
加入二阶滞后项后，AIC和BIC都上升了

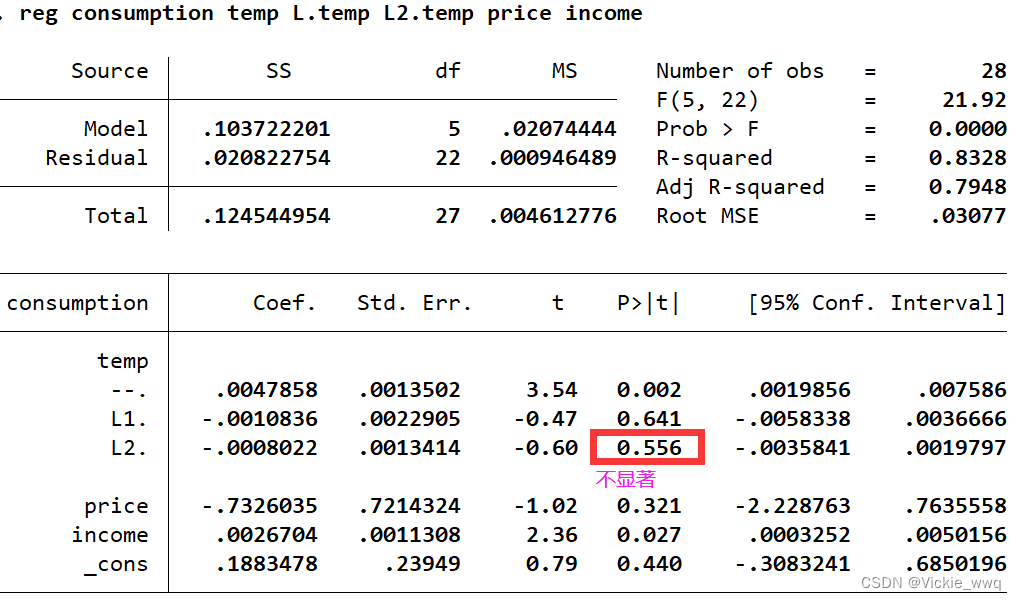
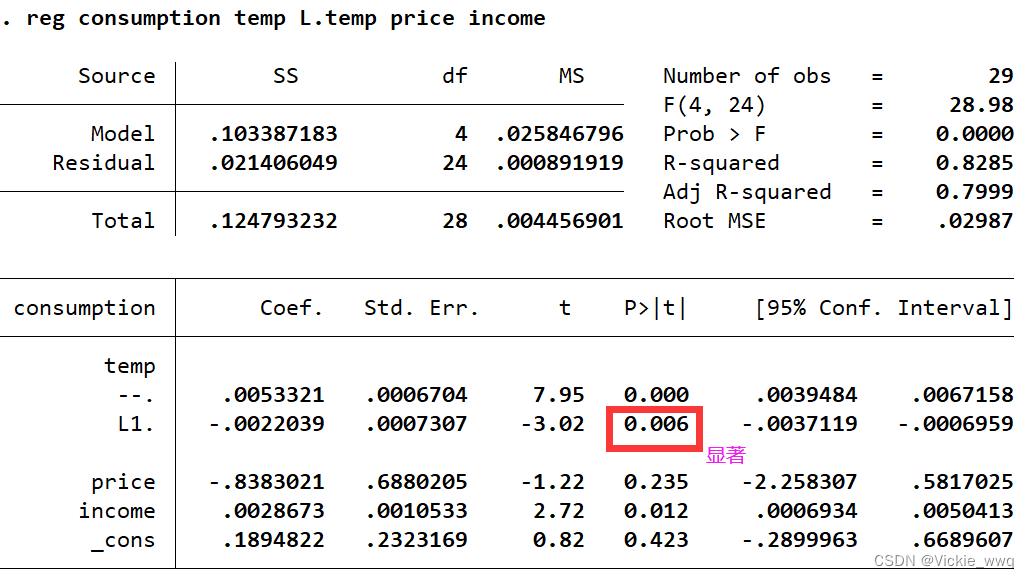
9.5 对函数形式的检验

假设真实模型为：
$$y=\alpha +\beta x+(\gamma x^2+\epsilon )$$
其中，$Cov(x,\epsilon )=0$，而平方项$\gamma x^2$被遗漏。
解释变量与扰动项相关：$Cov(x,\gamma x^2+\epsilon )=\gamma Cov(x,x^2)+Cov(x,\epsilon )=\gamma Cov(x,x^2)\ne 0$
因此遗漏高次项也会导致遗漏变量偏差。

Ramsey’s RESET 检验
①辅助回归：$y=\alpha +\beta x_1+\gamma x_2+{\delta }_2{\hat{y}}^2+{\delta }_3{\hat{y}}^3+{\delta }_4{\hat{y}}^4+\epsilon$
对$H_0:{\delta }_2={\delta }_3={\delta }_4=0$作$F$检验。
如果拒绝$H_0$，则说明模型中应有高次项，但不能提供具体遗漏哪些高次项的信息；反之，如果接受$H_0$，则可使用线性模型。
②辅助回归：$y=\alpha +\beta x_1+\gamma x_2+{\delta }_2{x}_1^2+{\delta }_3{x}_2^2+{\delta }_4{x}_1{x}_2+\epsilon$
检验$H_0:{\delta }_2={\delta }_3={\delta }_4=0$

如何确定回归方程的函数形式，最好从经济理论出发。在缺乏理论指导的情况下，可先从线性模型出发，然后进行RESET检验，看是否加入非线性项。

在Stata中作完回归，进行RESET检验的命令为estat ovtest,rhs
ovtest：omitted variable test，因为遗漏高次项的后果类似于遗漏解释变量。
选择项 rhs ：表示用解释变量的幂为非线性项，即②。默认①。

grilic.dta

qui reg lnw s expr tenure smsa rns
estat ovtest
estat ovtest,rhs
gen expr2=expr^2
reg lnw s expr expr2 tenure smsa rns
estat ovtest,rhs

事实上，在本例中，最重要的模型设定误差乃是遗漏了对个人能力的度量，将在第10章进一步讨论。

9.6 多重共线性

在Stata上画VIF关于$R_k^2$的图像
twoway function VIF=1/(1-x),xtitle(R2) xline(0.9,lp(dash)) yline(10,lp(dash)) xlabel(0.1(0.1)1) ylabel(10 100 200 300)




在Stata中作完回归后，可使用如下命令计算各变量的VIF
estst vif

grilic.dta

use "D:\a_DUFE\000master_gogogo\stata相关\陈强_计量经济学及Stata应用\Data-Finished-本科计量\grilic.dta"
reg lnw s expr tenure  smsa rns
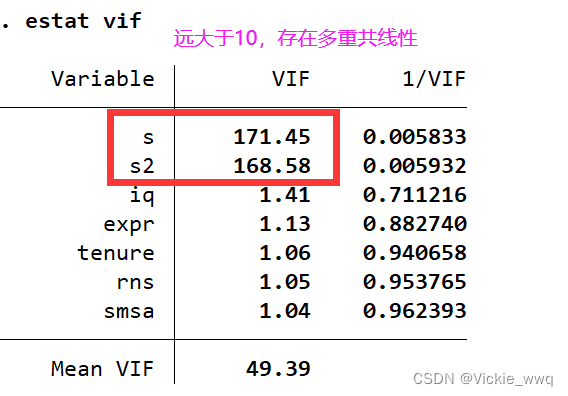
estat vif
gen s2=s^2
reg lnw s s2 expr tenure smsa rns
estat vif
reg s2 s
sum s
gen sd=(s-r(mean))/r(sd)
gen sd2=sd^2
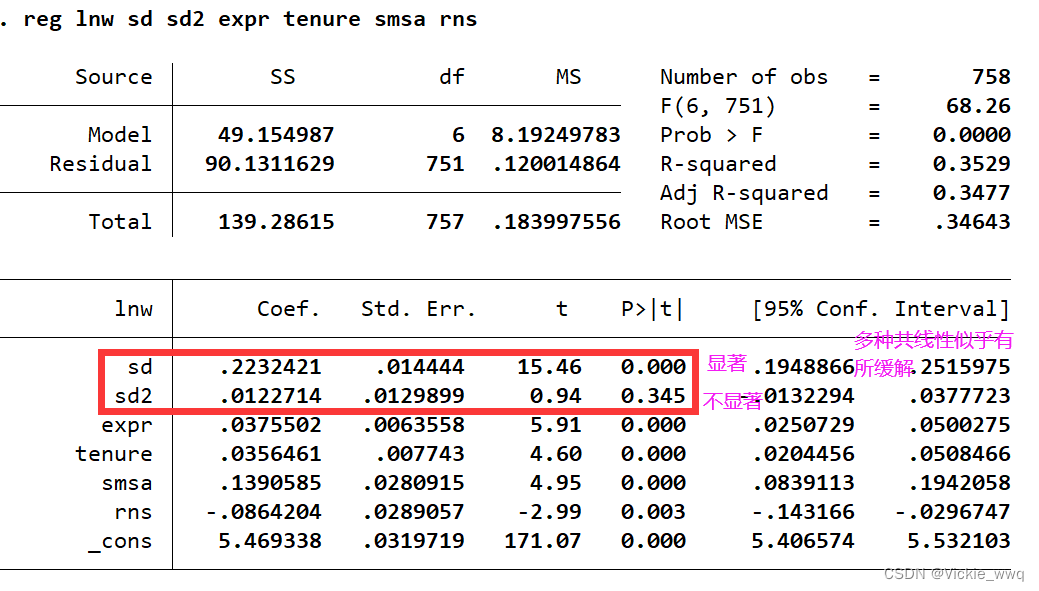
reg lnw sd sd2 expr tenure smsa rns
estat vif
reg sd2 sd
reg lnw sd  expr tenure smsa rns
dis  .2290816/2.231828
reg lnw s expr tenure iq smsa rns

P.S.下面的图有下错误，不想改了（任性ing）





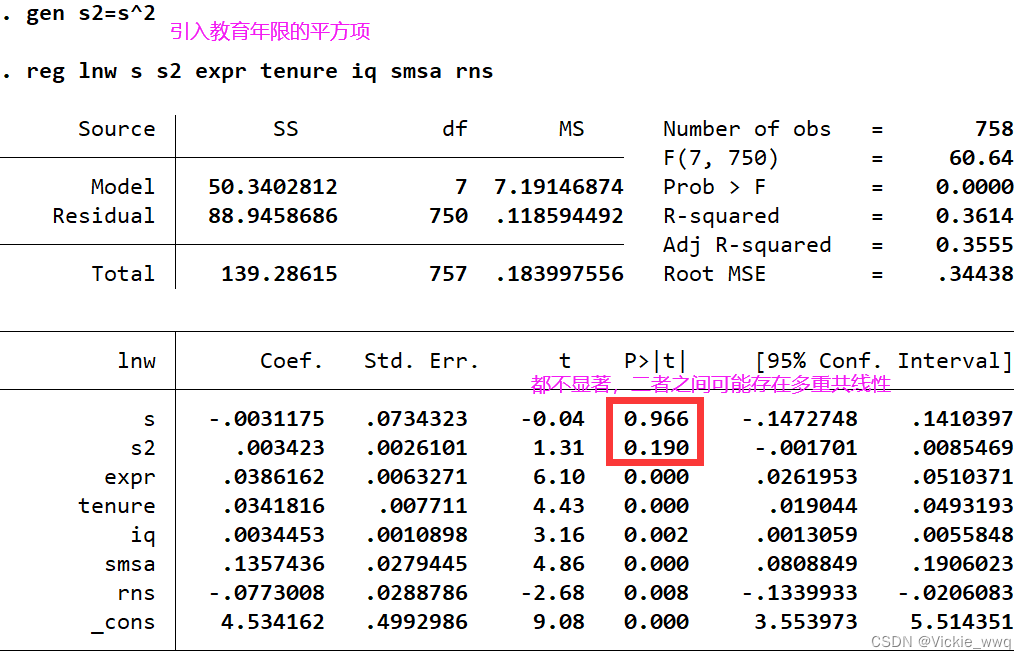
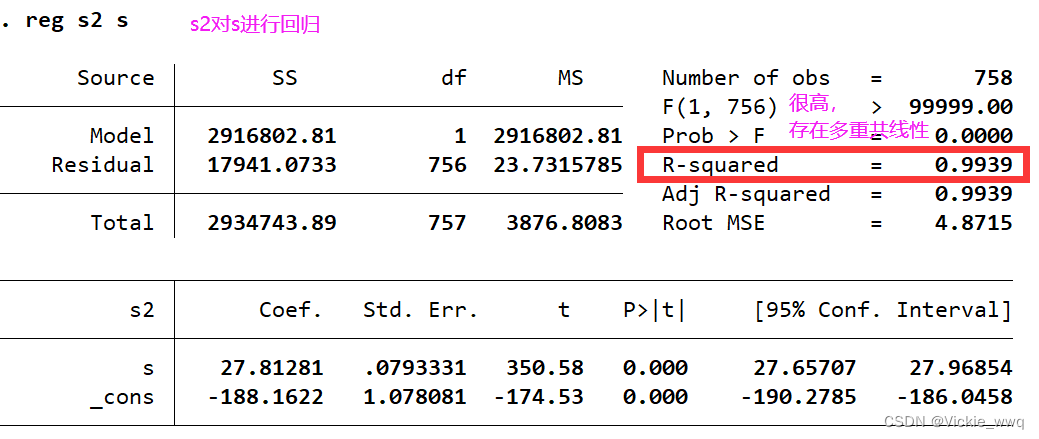
一个可能的解决办法是将变量标准化，即减去均值，除以标准差
$$\tilde{x}\equiv \frac{x-\overline{x}}{s_x}$$

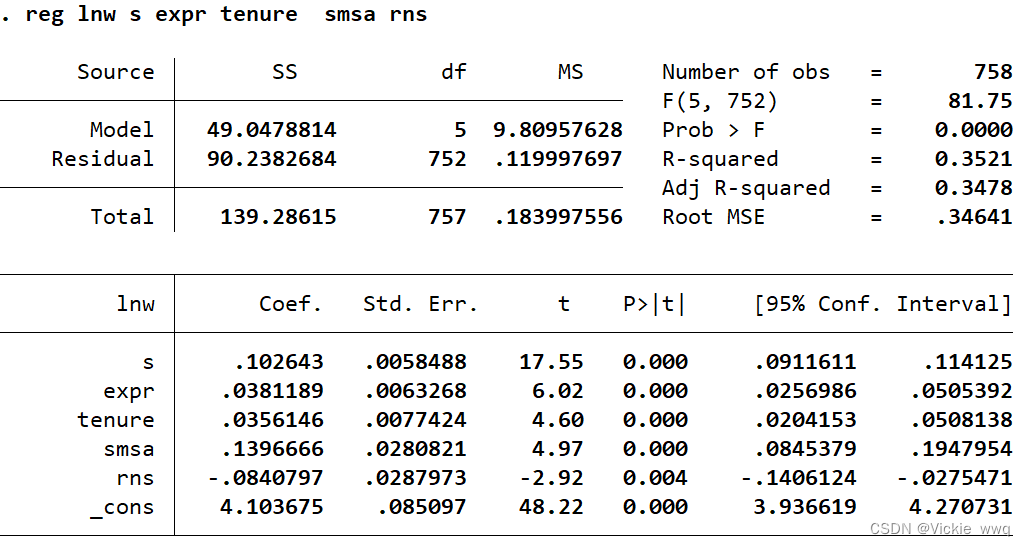
9.7 极端数据

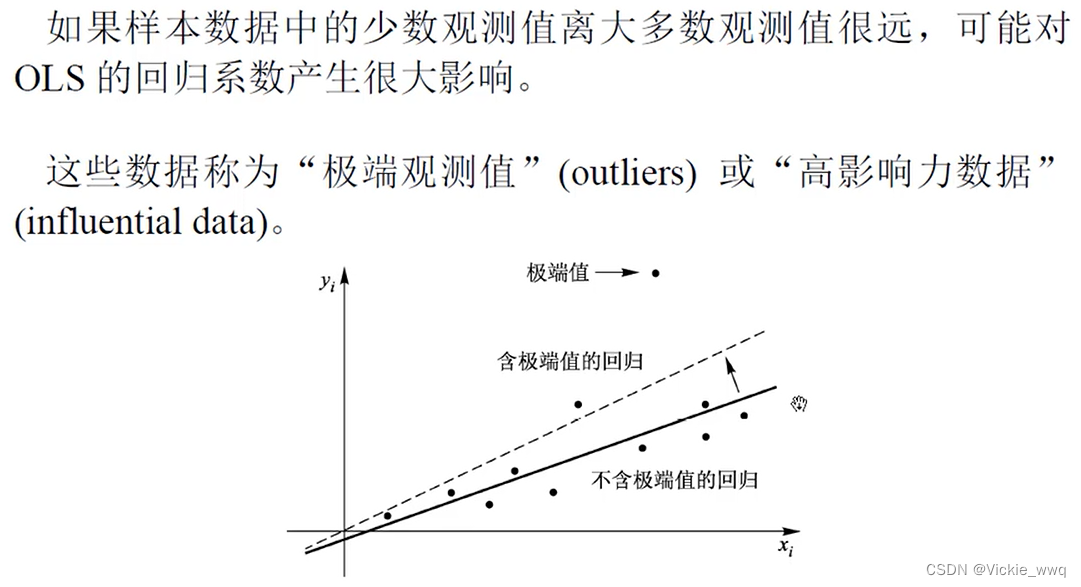
nerlove.dta
进行回归，人为地构造一个极端值，再进行回归。比较的回归结果。
去掉人造极端值。对比回归结果。

use "D:\a_DUFE\000master_gogogo\stata相关\陈强_计量经济学及Stata应用\Data-Finished-本科计量\nerlove.dta"
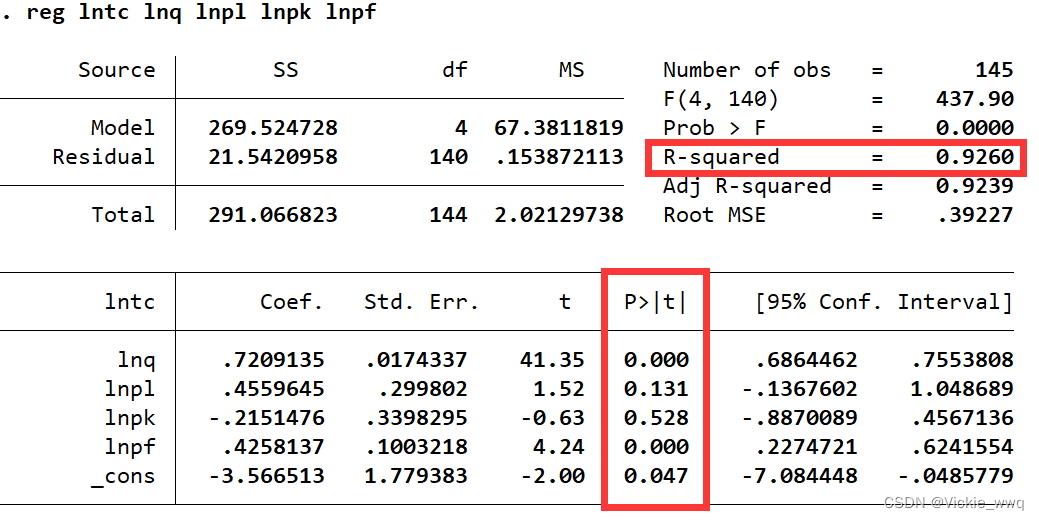
reg lntc lnq lnpl lnpk lnpf
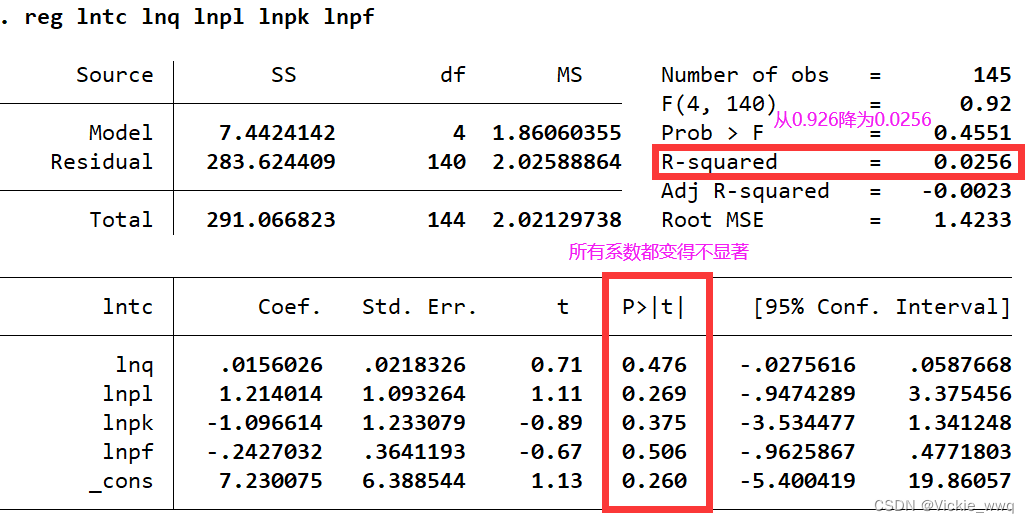
replace lnq=lnq*100 if _n==1	//将第一个观测值的产量对数乘以100
reg lntc lnq lnpl lnpk lnpf
reg lntc lnq lnpl lnpk lnpf if _n>1	//去掉人造极端值

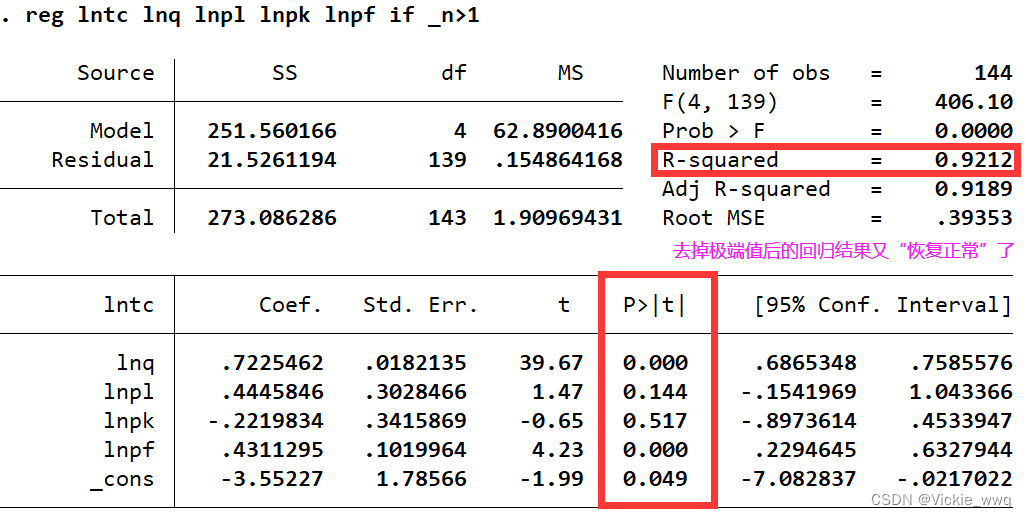
如何发现极端数据？？？

• 对于一元回归，可以通过画$(x,y)$的散点图来直观地考察是否存在极端观测值。但画图的方法对于多元回归则行不通。

• 某个观测值的影响力可通过去掉此观测值对回归系数的影响来衡量。

$\hat{\beta }$：全样本的OLS估计值
${\hat{\beta }}^{(i)}$：去掉第$i$个观测值后的OLS估计值

我们关心$(\hat{\beta }-{\hat{\beta }}^{(i)})$的变化幅度以及如何决定。

定义：第$i$个观测数据对回归系数的“影响力”或“杠杆作用”为 $le{v}_i\equiv {\mathbf{x}}_{\mathbf{i}}^{{}^{\prime }}({\mathbf{X}}^{{}^{\prime }}\mathbf{X}{)}^{-1}{\mathbf{x}}_{\mathbf{i}}$
lev_i和$(\hat{\beta }-{\hat{\beta }}^{(i)})$的关系：
$$\hat{\beta }-{\hat{\beta }}^{(i)}=\left(\frac{1}{1-le{v}_i}\right)({\mathbf{X}}^{{}^{\prime }}\mathbf{X}{)}^{-1}{\mathbf{x}}_{\mathbf{i}}{e}_i$$
lev_i越大，则$(\hat{\beta }-{\hat{\beta }}^{(i)})$的变化越大

lev_i满足：
（1）0≤lev_i≤1，（i=1，…，n）
（2）$\sum _{i=1}^{n}le{v}_i=K$（解释变量个数），影响力lev_i的平均值为$K/n$

• 如果某些数据的lev_i比平均值$K/n$高很多，则可能对回归系数有很大影响。

在Stata中作完回归后，计算影响力lev_i的命令为
predict lev,leverage
变量名lev可自行命名

nerlove.dta

use "D:\a_DUFE\000master_gogogo\stata相关\陈强_计量经济学及Stata应用\Data-Finished-本科计量\nerlove.dta"
qui reg lntc lnq lnpl lnpk lnpf
predict lev,leverage
sum lev
dis r(max)/r(mean)
gsort - lev	//将观测值按变量lev的降序排列
list lev in 1/3
replace lnq=lnq*100 if _n==1
qui reg lntc lnq lnpl lnpk lnpf
predict lev1,leverage
sum lev1
dis r(max)/r(mean)

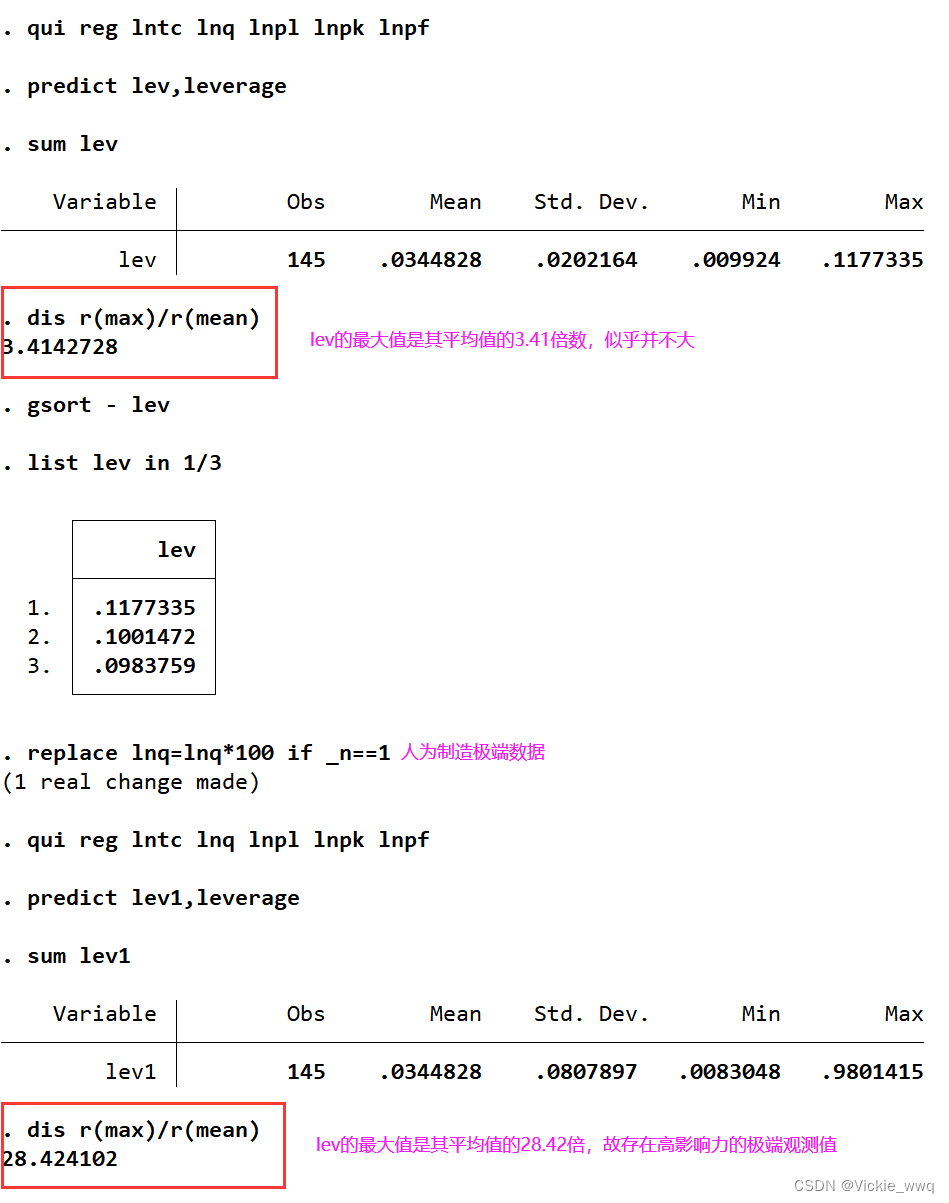
如果发现存在极端数据，应该如何处理呢？？

• 首先，应仔细检查是否因数据输入有误而导致极端观测值。

• 其次，对出现极端观测值的个体进行背景调查，考察是否由与研究课题无关的特殊现象所致，必要时可以删除极端数据。

• 最后，比较稳健的做法是同时汇报“全样本”与删除极端数据后的“子样本”的回归后果，让读者自己做判断。

9.8 虚拟变量

比较好理解的一节。偷懒一下，nonono，这是节约时间！(义正言辞)

9.9 经济结构变动的检验

对于时间序列而言，模型系数的稳定性是很重要的问题。如果存在“结构变动”，但未加考虑，也是一种模型设定误差。

例子
假设要检验中国经济是否存在1978年发生结构变动

分成两个时期。
两个时期对应的回归方程可分别记为：
$$\begin{gathered} y_t={\alpha }_1+{\beta }_1{x}_t+{\epsilon }_t（1950\le t<1978） \\ {y}_t={\alpha }_2+{\beta }_2{x}_t+{\epsilon }_t（1978\le t\le 2010） \end{gathered}$$
原假设：经济结构在这两个时期内没有变化。$H_0:{\alpha }_1={\alpha }_2,{\beta }_1={\beta }_2$
共有两个约束。更一般地，如果有K个解释变量（包含常数项），则$H_0$共有K个约束。

无约束的情况：对两个时期分别进行回归。
有约束的情况：即$H_0$成立的情况下，将模型合并。
$$y_t=\alpha +\beta x_t+{\epsilon }_t（1950\le t\le 2010）$$
其中，$\alpha ={\alpha }_1={\alpha }_2,\beta ={\beta }_1={\beta }_2$

传统的“邹检验”
通过三个回归来检验“无结构变动”的原假设

• 回归整个样本，$1950\le t\le 2010$，得到残差平方和，记为$SS{R}^{\ast }$
• 回归第1部分子样本，$950\le t<1978$，得到残差平方和$SS{R}_1$
• 回归第2部分子样本，$1978\le t\le 2010$，得到残差平方和$SS{R}_2$

将整个样本一起回归为“有约束OLS”，其残差平方和为$SS{R}^{\ast }$。
而将样本一分为二，分别进行回归则为“无约束OLS”，其残差平方和为$SSR=SS{R}_1+SS{R}_2$

因为有约束OLS的拟合度比无约束OLS更差，所以$SS{R}^{\ast }\ge SSR=SS{R}_1+SS{R}_2$
根据第5章似然比检验原理的$F$统计量，检验结构变动的$F$统计量：
$$F=\frac{(SS{R}^{\ast }-SS{R}_1-SS{R}_2)/K}{(SS{R}_1+SS{R}_2)/(n-2K)}\sim F(K,n-2K)$$
其中，$n$为样本容量，$K$为有约束回归的参数个数（含常数项）。

引入虚拟变量，并检验所有虚拟变量以及其与解释变量交叉项的系数的联合显著性
比如，对于$K=2$的情形，可进行如下回归：
$$y_t=\alpha +\beta x_t+\gamma D_t+\delta D_t{x}_t+{\epsilon }_t$$
然后检验连个假设$H_0:\gamma =\delta =0$。此检验所得$F$统计量与传统的邹检验完全相同。因此，虚拟变量法与邹检验是等价的。

与传统的邹检验相比，虚拟变量法的优点包括：
（1）只需生成虚拟变量即可检验，十分方便。
（2）邹检验是在“球形扰动动项”（同方差、无自相关）的假设下得到的，并不适用于异方差或自相关的情形。在异方差或自相关的情况下，仍可使用虚拟变量法，只要在估计方程时，使用异方差自相关稳健的HAC标准误即可。
（3）如果发现存在结构变动，邹检验并不提供究竟是截距项还是斜率变动的信息（至少需要再作一个邹检验），而虚拟变量法则可同时提供这些信息。

consumption.dta

use "D:\a_DUFE\000master_gogogo\stata相关\陈强_计量经济学及Stata应用\Data-Finished-本科计量\consumption.dta"
twoway connect c y year,msymbol(circle) msymbol(triangle)
twoway connect c y year,msymbol(circle) msymbol(triangle) xlabel(1980(10)2010) xlin(1992)
//邹检验
reg c y
scalar ssr=e(rss)
reg c y if year<1992
scalar ssr1=e(rss)
reg c y if year>=1992
scalar ssr2=e(rss)
di((ssr-ssr1-ssr2)/2)/(ssr1+ssr2/32)
//虚拟变量法
gen d=(year>1991)
gen yd =y*d
reg c y d yd
test d yd
qui reg c y
estat imtest,white  //怀特检验，是否存在异方差。存在异方差
tsset year	//设定变量year为时间变量
estat bgodfrey	//BG检验，是否存在自相关。存在自相关
dis 36^(1/4)	//计算HAC标准误的截断参数
newey c y d yd,lag(3)  //进行Newey-West回归。根据上一行代码的结果，截断参数设为3
test d yd

9.10 缺失数据与插值

又偷懒一下



线性插值的Stata命令为
ipolate y x,gen(newvar)
“ipolate”表示interpolate，即将变量y对变量x进行线性插值，并将插值的结果记为新变量newvar

consumption.dta

use "D:\a_DUFE\000master_gogogo\stata相关\陈强_计量经济学及Stata应用\Data-Finished-本科计量\consumption.dta"
gen y1=y
replace y1=. if year==1980|year==1990|year==2000|year==2010 //人为剔除数据
//做法一：直接用y1对year进行线性插值，结果记为y2
ipolate y1 year,gen(y2)
//做法二：先对y1取对数，进行线性插值，再取反对数，结果记为y3
gen lny1=log(y1)
ipolate lny1 year,gen(lny3)
gen y3=exp(lny3)
//对比两种方法的效果
list year y y2 y3 if year==1980|year==1990|year==2000|year==2010

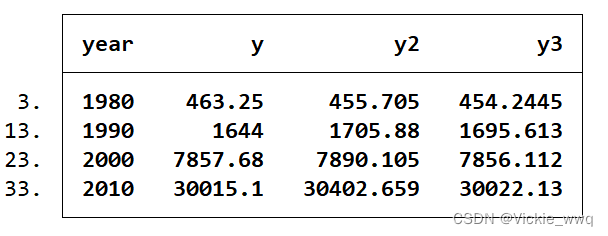
直接插值的结果y2倾向于高估真实值y，而整体估计效果不如先取对数再插值的结果y3（1980年的结果是个例外）。

9.11 变量单位的选择