融合ELO机制的销售能力评估方案

ELO排位赛算法

一. ELO机制

    ELO等级分制度是由匈牙利裔美国物理学家Elo创建的一个衡量各类对弈活动选手水平的评分方法，是当今对弈水平评估的公认的权威方法。被广泛应用于国际象棋、围棋、足球等运动，以及很多网游与电子竞技产业。游戏界比较著名的应用有： WOW（魔兽世界）、DOTA、LOL。

    ELO计算方法:

Ra：A玩家当前的积分
Rb：B玩家当前的积分
Sa：实际胜负值，胜=1，平=0.5，负=0
Ea：预期A选手的胜负值：$Ea=\frac{1}{1+10^{\frac{R_b-R_a}{D}}}$
Eb：预期B选手的胜负值：$Eb=\frac{1}{1+10^{\frac{R_a-R_b}{D}}}$

因为E值也为预估，则Ea+ Eb=1
R’a=Ra+K（Sa-Ea），
其中默认K=32， D=400，均为超参

二. 销售能力抽象为ELO排位赛设计

2.1 基础设计

假如一共有ABCDE个销售，每个人基础分数1500分, 新销售加入也是基础分数1500分
结算周期：1day（假如1day代表1期）

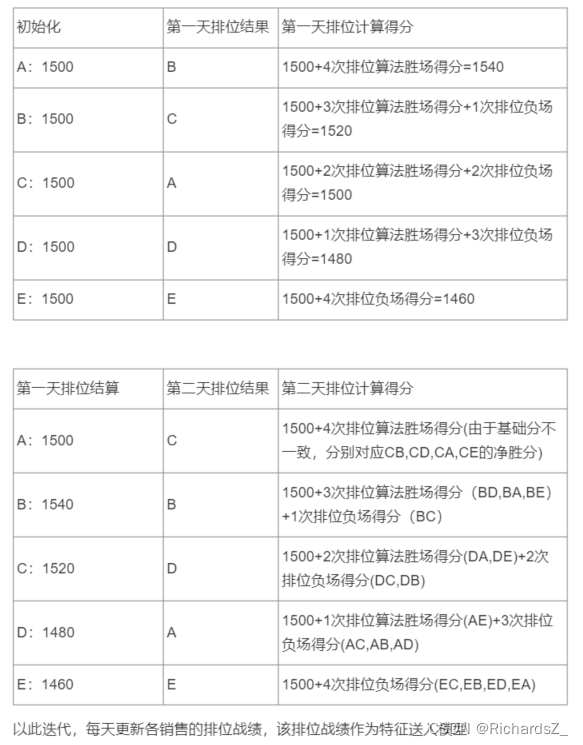
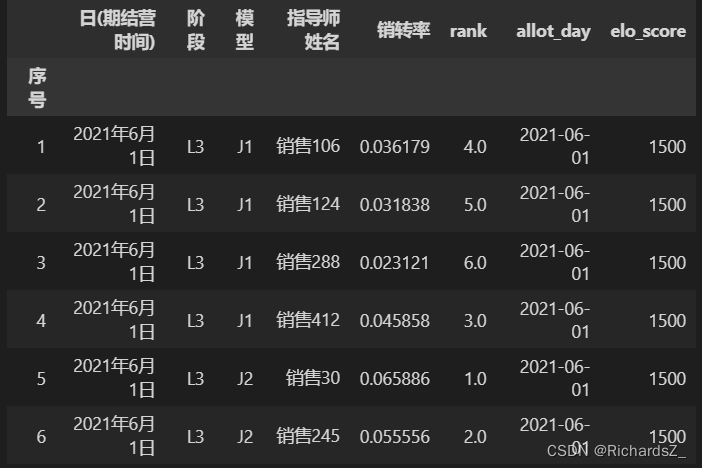
配置赛季初为：2021-06-01，所有销售初始分均为1500分

2.2 存在问题

问题1：新销售存在冷启动问题；

问题2：转化率存在不置信的问题，例如极端情况，新销售分配了2单，成交了一单，转化率为50%；

问题3：比赛周期固定，导致销售相对能力不稳定，例如比赛周期设定的短，分配量不足，转化率不置信；比赛周期长，销售受休假调整，生活变故等因素，转化率仍存在波动。

问题4：销售之间的多人竞技若视为两两对抗，将会导致赛季表现优异者一赢通赢，分数爆炸增长，而赛季表现差者，一输皆输，分数剧烈下滑。

问题5：没有考虑胜负程度，例如转化率3.5%的销售胜出转化率3.4%的销售，与3.5%胜出1.5%的奖惩是一样的。

三. 优化措施

3.1 如何解决新销售存在冷启动问题

新老人动态K值调整

目标：解决问题1，新人加入，期望分数快速收敛

若销售参赛时间<=9个赛日（45-63days）: K=36
若销售参赛时间>9个赛日: K=64
若销售第一次参赛：K=28
auc：0.528 -> 0.532

假设检验衡量赢的程度

目标：解决问题5

● 假设检验法（TODO），如z_检验 -> 用于判断两组均值（即转化率）是否存在显著性差异
目前只有聚合后的转化率数据，对于假设检验缺少核心数据

● 基于二组率样本量估算求得显著性水平法

原规则，赢：1， 平：0.5， 输：0
若p1>p2，则显著性水平=赢的程度，把赢的程度映射到[0.5-1]区间
若p1<p2, 则显著性水平=输的程度，把输的程度映射到[0-0.5]区间

如p1=0.036, p2=0.031，通过计算得知，显著性水平=0.45（即赢的程度）
k = (1-0.5)/(0.95-0)
映射后的值=0.5+k*显著性水平=0.73

如p1=0.031, p2=0.036，通过计算得知，显著性水平=0.45（即输的程度）
映射后的值=0.5-k*显著性水平=0.26

auc从0.528->0.532

二组率差异性样本量计算

3.2 如何解决转化率存在不置信的问题

ELO升级为MultiELO

    基础ELO对于预期A选手的胜负值为$Ea=\frac{1}{1+10^{\frac{R_b-R_a}{D}}}$，这在1v1场景下是没有异议的。但对于多人竞技场景下（n v n），两两选手都会进行一次比赛，那么一共会进行$C_n^2=\frac{n(n-1)}{2}$次竞技。

痛点：传统ELO会本轮多人竞技抽象为$\frac{n(n-1)}{2}$场1v1的胜负，那么导致的结果是，本轮第一名赢了其余所有选手，他本轮的净胜分会迎来爆炸级增长，同样的，本轮最后一名选手输给了其余所有选手，他的净胜分会迎来剧烈下跌（甚至负分）。这样的剧烈波动是我们不想看见的。

MutiELO:

• 预期分改良

在多人比赛结果基础上，将预期A选手的胜负值进行标准化，如下图所示

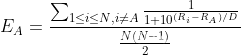
• 实际胜负值改良

传统实际胜负值为1，0.5和0。

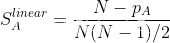
N:本轮参与比赛的人数
pA: A玩家本轮的排位自然位置(1 for first place, 2 for second, and so on)

举例而言，本轮5名玩家参赛，本轮结束后，根据比赛结果排位，每个对应位置的玩家实际胜负值为[0.4, 0.3, 0.2, 0.1, 0]，使用本方法，则认为第一名赢第二名的程度，与第二名赢第三名的程度时一致且公平的。

https://github.com/djcunningham0/multielo