隐式马尔科夫模型中的Baum-Welch算法详解

前言

本篇分别从Baum-Welch算法流程和EM算法中所涉及公式的推导这两个方面来介绍Baum-Welch算法，旨在读者能理解如何使用Baum-Welch算法，以及掌握算法步骤中公式的来龙去脉。
为了保证阅读效率，一些前置知识点会被安排在文章末尾。
有任何的建议欢迎在评论区留言，随时看随时修改哦~谢谢大家【鞠躬

一、Baum-Welch算法流程

1. 输入训练观测数据O=(o1,o2,…,oT). 同时初始化模型参数，从n=0开始，选取a0，b0，π0，得到模型λ0

2. 递推n，n=1,2,…,n
   
   接着用观测数据O和λn开始计算
   图中公式的γ和ζ将在EM公式推导中介绍。
   3)得到模型参数λ(n+1)
   根据第二步中即将展现的推导可知，在n+1时可以获得极大值。
   
   第四步需要我们自己设置2个阈值，用来停止迭代。

二、EM算法公式推导

1）EM算法基础概念

首先，假设我们有许多组模型参数，λ1~λn，求每一个模型和O匹配的可能性（概率）P(O|λ)，那么可能性最大的那个就最有可能成为隐式马尔科夫模型的参数。
O是观测序列，I是状态序列，λ是参数，λ中有3个子参数，分别是

同时隐式马尔科夫模型公式在EM算法中的意义为：

EM算法，最大似然估计，简单的说就是根据结果找出最有可能的条件。
隐式马尔科夫模型可以通过EM算法实现其参数学习。EM算法在隐式马尔科夫模型学习中的具体体现就是Baum-Welch 算法。
EM算法可以分成两个步骤，1：E步骤；2：M步骤。

2）E步骤

1）首先先进行初始化。
观测数据O=(o1,o2,…,oT), 所有隐数据写成I=(i1,i2,…,iT),确定完全数据【观测和状态在一起就是完全数据，借用完全数据的公式求这里的不完全数据(I是隐数据)】(O,I)=(o1,o2,…,oT,i1,i2,…,iT).的对数似然函数logP(O,I|λ)
在这里我们引入一个函数

第一个λ是表示要极大化的参数，第二个横线λ是参数当前的估计值，每一次的迭代都是在求Q函数及其极大值。
定义：完全数据的对数似然函数，在给定观测数据O,和当前参数横线λ下，隐数据I的可能性的期望称为Q函数。
Q函数在E步骤中就是求到函数内两个λ。9.11是Q函数之前的样子，E是求和符号，Z是I θ是λ，Y是O 展开就变成10.33了

【极大似然估计值】也就是【最大可能性的条件】。对数似然函数（9.12）和下面这一行很像（10.32）。

之后用琴声不等式得到下界，E(φ(x))≥ φ(E(x)）,琴声不等式得到的下界会更加松【这是官方说法】更加靠下，所以在迭代上升时，上升空间更多。在优化尺度迭代中同样用到了琴生不等式，

此时只要等式右边【下界】变大左边一定变大，如果右边是极大值了，左边也一定是极大值了。

对于一个θi找到最大的θ，也就是最符合θi的参数，将其作为θ（i+1）放入下次迭代。所以对于θi来说，θ（i+1）总是极大的。

上图中9.17的第二行，是由第一行L（θi）展开以后log加法转乘法与第二项分母相消得来。
至此，Q函数的公式推完了，让我们继续来看E步骤的后续。

这个公式要注意几点不一样的，对数只取前面一部分。
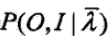要放在log的外面。
第二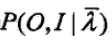，是一个确定的值，在0到1之间，根据横线λ算出。根据9.17的公式，10.33就是在对隐函数I求期望值。

这里πi1是初始点，bi1观测概率，o1是当前观测，ai1i2是状态转移概率。把这个代入Q再展开

λ被展开成三个参数【λ参数的调用就是用到哪个调哪个，但是存放是一起存放的】，log可以吧乘转为加法。

3）M步骤

EM算法的M步，就是分别计算刚刚3项，然后对各项分别极大化，这里统一使用拉格朗日乘子法。
使用拉格朗日乘子法的原因是，拉格朗日乘子法可以对有约束等式求极值，具体在前置内容的b点中。

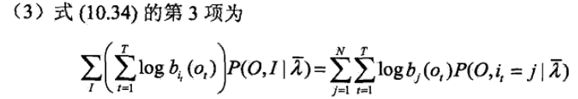
上面三个公式最后的结果分别是

这时我们引入2个变量：




在ζ中使用的前后项的递推计算，所以我们使用

最后对γ和ζ的期望值进行归纳

随后我们将γ和ξ代入三个拉格朗日之后的参数公式

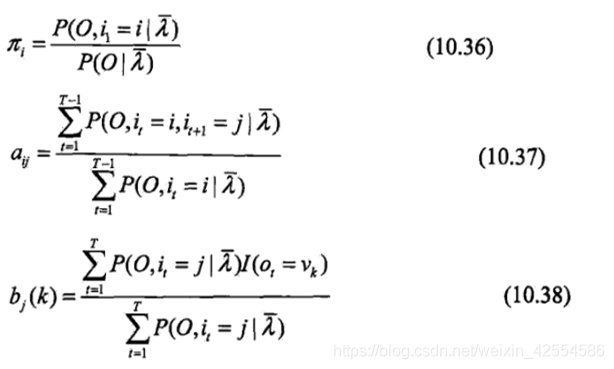
接着得到

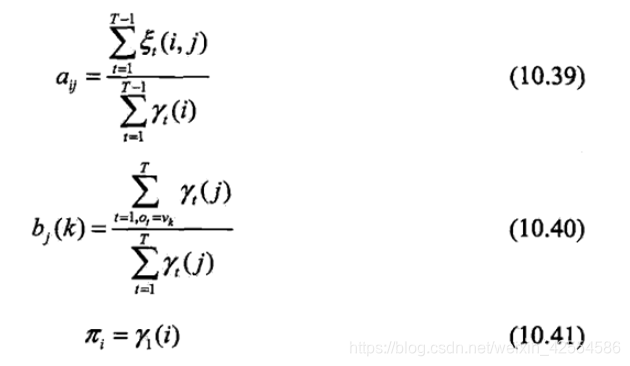
10.39、10.40、10.41便是BW算法流程中的三个公式形式。

三、前置内容

a)条件概率和联合概率

先讲一个知识点，条件概率和联合概率
P(A|B)是在B发生的情况下，A发生的概率
P(A,B)是A,B同时发生的概率
乍一看是一样的。
举个例子
52张扑克牌。我们要找出红色4，红色四分为桃心和方片，所以有两张
P(4|红) 是先分出红黑，再找出4,

所以P(4|红)=1/13
P(4,红)是在全部牌中分出红色4
P(4,红)= 1/26
因为总池子不一样，条件概率的池子由条件的个数决定，联合概率的池子是不带条件的全体。
但是在不知道准确个数，没法通过比例的方法求解时，条件概率必须通过朴素贝叶斯才能求得，
否则简单相乘求的就是联合概率。

b)拉格朗日乘子法的理解

在求解最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。
一般情况下，最优化问题通常是指对于给定的函数f(x)，求其在指定作用域上【作用域即约束】的全局最小值（最小值与最大值很容易转化，所以都一样，比如两边求倒数）
具体推导不展开，但是拉格朗日乘子法可以将带有约束的等式转化为无约束等式，这就是在等式约束时使用拉格朗日乘子法的原因。

c)隐数据

上文中E步骤中的隐数据为HMM模型本身自带，因为HMM模型本身就有未知条件和未知参数。

d)完全数据

上文说过完全数据必须要观测和状态同时存在且显式，所以HMM模型是不完全数据，但是如果我们需要确定选用什么样的概率模型，就必须要先假设数据形态为完全数据。举个例子，在上文中完全数据的形态是对数似然函数，所以我们选用对数似然函数作为不完全数据的概率模型。

四、引用

1）李航 (2011). 《统计学习方法》