本文主要是介绍2022美赛C题股票投资策略回顾讲解,教你正确打数学建模比赛,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
比赛结束,所以我才正式发一下自己的思路,美赛国赛我不会发比赛思路。我们来聊一聊美赛C题到底在怎么理解?
首先说一下我也犯的大忌:大家都知道我们大多数数学建模都是英文版的,题目也是英文,习惯性用软件就把英文直接机器翻译成中文(如果运气不好,很有可能会一些专业词语翻译错误,导致对题目理解和处理有了偏差,浪费了时间,但是说实话题目英语难度确实简单,高中水平即可读懂)
个人英语不佳,懒得读英文,拿到题目我就直接用翻译软件把它全部机翻了,节约时间,这里推荐一款翻译挺不错的软件:Deel,个人英语不佳,懒得读英文,拿到题目我就直接用翻译软件把它全部机翻了,节约时间,这里推荐一款翻译挺不错的软件:Deel,可以通过文末查看如何领取。
先看背景:
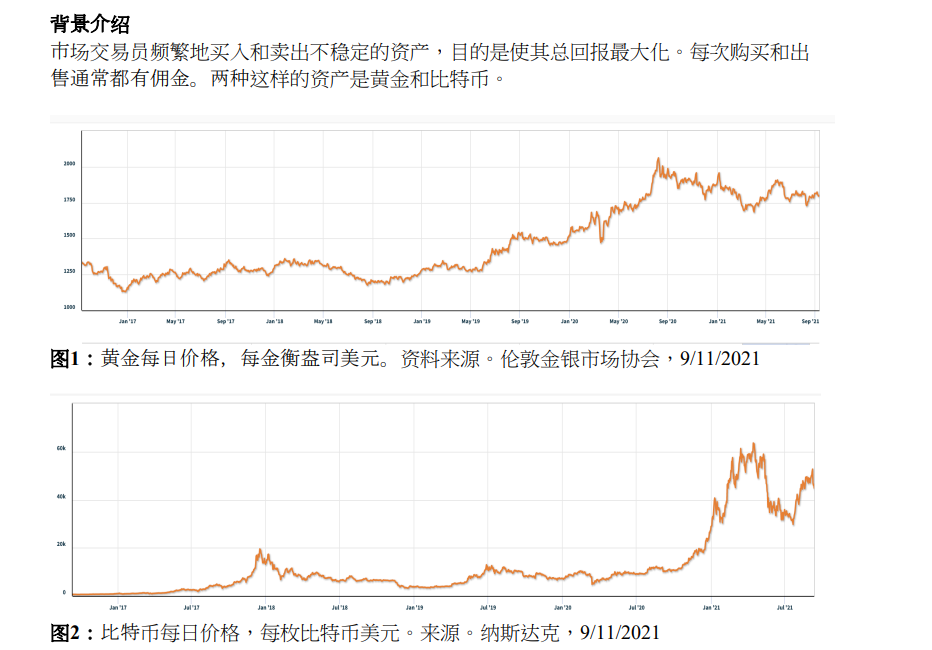
背景配上两张图简直把这个题目说得明明白白,这就是一个股票投资策略问题,要想办法赚最多的钱,就是这个意思。当然读了背景,我们还并不知道什么思路。
1.1 第一问
继续往下读题:

读完题,我们首先要知道他要问的是什么,通俗说一下就是:给你1000美元拿去对黄金和比特币进行投资,投资开始时间是2016年11月9日,结束时间是2021年9月9日,你需要用一个构建一个模型保证使用你的模型能赚最多的钱,注意的是股票的买和卖都要扣除手续费,分别为1%和2%。
题目种还说到黄金和比特币的数据在那两个文件夹,值得注意的是黄健只能在开市的日子交易,我们来看一下数据:
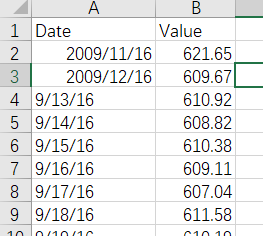
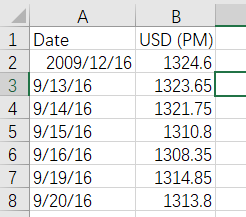
可以看到数据就是简单的二维,一个变量一个自变量的形式,数据并不复杂,暂时我们还不说到数据处理,读题我们就是为了心里有个数。看到这如此简单的数据,心里是真坦荡。
1.2 第二问
读题:

证明我们上面的策略是最佳策略?那不就是证明我们的策略是最能赚钱的吗,这能怎么证明?应该有一个类似最佳标准。所以目前问题还是主要第一问。
这篇关于2022美赛C题股票投资策略回顾讲解,教你正确打数学建模比赛的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




