Basal Glucose Control in Type 1 Diabetes using Deep Reinforcement Learning: An In Silico Validation

Abstract

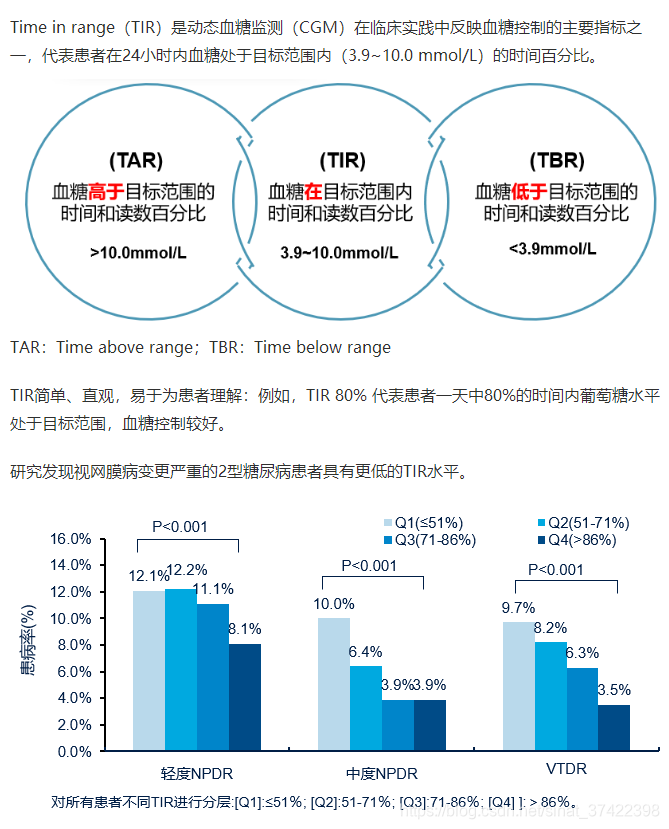
\qquad 1型糖尿病(T1D)患者需要定期外源性输注胰岛素，以维持其血糖浓度在适当的治疗目标范围内。虽然人工胰腺和连续血糖监测在实现闭环控制方面已经被证明是有效的，但由于血糖动力学的高度复杂性和技术的局限性，仍然存在重大挑战。在这项工作中，我们提出了一种新的深度强化学习模型，用于 单激素（胰岛素）和 双激素（胰岛素和胰高血糖素）的给药。特别的，delivery strategies 是用了利用了 dilated recurrent neural networks （DRNN） 的 double Q-learning 。在设计和测试过程中，我们应用了 FDA-accepted UVA/Padova Type 1 模拟器 。首先，我们进行长期的一般化的训练来获得一个人类模型（a population model）。然后，利用一个小数据集对模型进行个性化处理。结果显示，与标准的 有 低血糖暂停 的 基础率-大剂量疗法 （a standard basal-bolus therapy with low-glucose insulin suspension） 相比，单激素和双激素给药策略可以起到更好的血糖控制。具体的说，在成年人群体中（n=10），单激素控制时在目标范围 $[70,180]mg/dL$ 百分比从 $77.6\%$ 增加到 $80.9\%$，双激素控制增加到 $85.6\%$。在青少年人群中（n=10），单激素在目标范围内的百分比从 $55.5\%$ 增加到 $65.9\%$，双激素增加到 $78.8\%$。在所有情况下，观察到低血糖显著降低。
这些结果表明，使用深度强化学习是一种可行的方法，它以闭环控制的方式作用于 T1D。

Methodology

• percentage time：直译是时间百分比，

\qquad 在这一节，我们陈述了 deep RL 在基础血糖调控中 的闭环控制。然后，我们介绍了一个两步的框架，借鉴了 迁移学习，来探索单激素、双激素血糖控制在临床中的应用（在 in silico 平台上进行模拟临床试验）。
\qquad 特别的，Deep Q-learning 模型 被用于优化胰岛素和胰高血糖素的给药。胰岛素和胰高血糖素的给药行为被视为 随机策略（stochastic policy） 给出的 $action(a)$，血糖结果（如，percentage time in glucose target）被视为 $reward(r)$，生理参数被视为 $state(s)$。深层神经网络(DNN)被用作一个非线性函数逼近器来估计 action value，也被称为 DQN。与以往使用传统RL控制AP系统的方法不同，不需要 葡萄糖、胰岛素和胰高血糖素代谢的知识 。取而代之，用一堆 dilated recurrent layers 来处理多维时间序列数据。因为 扩大了感受野，所以 能够捕获 葡萄糖-胰岛素-胰高血糖素 复杂的动力学特性 ，如我们之前的研究所述[18,20]。附录中的7.1节解释了DRNN模型是如何在其他神经网络架构中选择的。
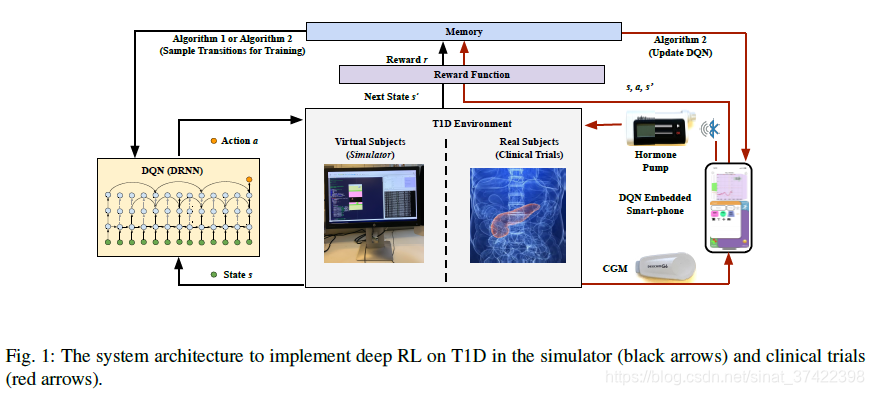
\qquad 图1概述了用于开发DQN控制器的系统架构，该控制器在 in silico 环境下对T1D进行了评估，并可能用于临床试验。算法1和算法2对应于2.2节中的两步学习框架。

2.1 Problem Formulation

\qquad T1D 的闭环基础血糖控制问题可以表示为一个带噪声的无限状态Markov决策过程，用五元组进行定义 $<S,\mathcal{P},A,R,\gamma >$，包含状态 $S$（即，生理状态physiological state），状态转换函数 $\mathcal{P}$，动作$A$（即，胰岛素和胰高血糖素的控制动作），回报函数 $R$，衰减因子 $\gamma \in [0,1]$。在环境中，agent 每一步（即，每个CGM测量）采取一个动作 $a\in A$，然后它的状态 $s\in S$ 根据 $\mathcal{P}$ 转换到 后继状态 $s^{\prime }$。给定状态选择动作是根据策略 $\pi$。目标是 最大化在每一步 $t$ 的 期望回报的积累 $r_t=R(s_t,a_t)$。一个 action-value(Q-function) $Q^{\pi }(s,a)$可以被定义为：

\qquad 优化的动作价值函数为 $Q^{\ast }(s,a)=ma{x}_{\pi }{Q}^{\pi }(s,a)$，它表示最大的价值，被定义：

2.1.1 Agent states

\qquad 在闭环葡萄糖控制问题中，我们从控制系统中收集多模态数据，如图1所示，以形成多维输入向量D来近似生理状态S。特别的， $D$ 包含 CGM 传感器测量的 真实连续血糖值 $G(mg/dL)$、通过智能手机记录的膳食摄入的碳水化合物含量 $M(g)$、由注射泵输送的激素剂量（包括 大剂量胰岛素 $B$、基础胰岛素 $Bas$）、胰高血糖素剂量 $C$ 。因此，我们得到：
D = { G , M , I , C } = [ d t + 1 − L , . . . , d t ] T ∈ R L × 4 D=\{G,M,I,C\}=[d_{t+1-L},...,d_t]^T \in \mathbb{R}^{\mathbb{L} \times 4} D={G,M,I,C}=[dt+1−L​,...,dt​]T∈RL×4
\qquad 其中， $L$ 是时间步长向量的长度，$I=B+Bas$ (Unit) 表示 大剂量 和 基础 胰岛素的和。近似观测值 $o_t=s_t+e_t$ (Unit) 考虑到了 在血糖测量 $G$ 、一餐中碳水化合物估计 $M$ 、大剂量胰岛素 $B$ 中的 errors 或者是 miss-estimations $e_t$。这里 $B$ 是用标准的 bolus 计算器 [28]计算出来的。从深层次的RL角度来看，这个问题可以看作是一个 agent 在连续的时间步骤中与环境交互。每5分钟，可以从环境获得一个观测值 $o_t$，并且可以根据 agent 的策略 采取一个行动 $a_t$。

2.1.2 Actions

\qquad 两种输注策略：
\qquad 对于佩戴胰岛素泵的 T1D 患者，通过调整基础胰岛素率的 action space：｛suspension of BR,0.5BR,BR, 1,5BR, 2BR｝。
\qquad 对于佩戴 双激素泵 的患者，其动作空间定义为：｛suspension of BR, 0.5BR, BR, 1,5BR, 2BR, delivering glucagon｝。
\qquad BR 的值 是 subject-specific（就是针对某个体是确定的，通过换算公式得知）和 确定的。基于之前的工作，我们将所有人的胰高血糖素剂量固定在 $0.3\mu g/kg$，并且限制每天给药总量不超过 $1mg$。

2.1.3 Rewards

\qquad 闭环血糖控制的理想性能是将血糖维持在70-180 mg/dL的目标范围内。通过使用一种旨在最大化 time in range (TIR) 和最小化低血糖的经验方法，采用下述分段函数作为奖励函数：

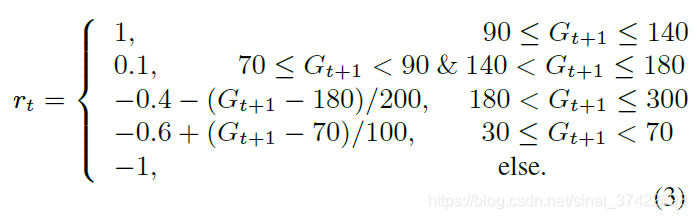
\qquad 如图2所示，如果下一状态的BG水平在目标范围内，agent 将获得正奖励，反之则获得负奖励。如果BG低于30mg /dL或高于300mg /dL，我们将终止算法并重新启动模拟器。不同的评估奖励功能在附录7.2部分给出。

2.2 Two-step Learning Framework

\qquad 首先，我们进行长期的一般性训练，以获得激素传递策略的群体模型。我们使用扩张型循环神经网络[18]来建模多维时间序列，包括葡萄糖水平、激素剂量和膳食摄入量。其他影响葡萄糖水平的输入，如体育锻炼，也可以考虑。为了训练模型，每次基础激素注射（每隔5分钟）都被认为是 agent 的一次行动，下一时间步的胰岛素水平被设置为奖励（Equation 3）。其次，通过对总体模型的权值进行初始化，得到了具有良好初始性能的模型。在迁移学习过程中，我们根据 personal characteristics 和 safety constraints，使用一个小的 subject-specific 的数据集个性化DQNs 。
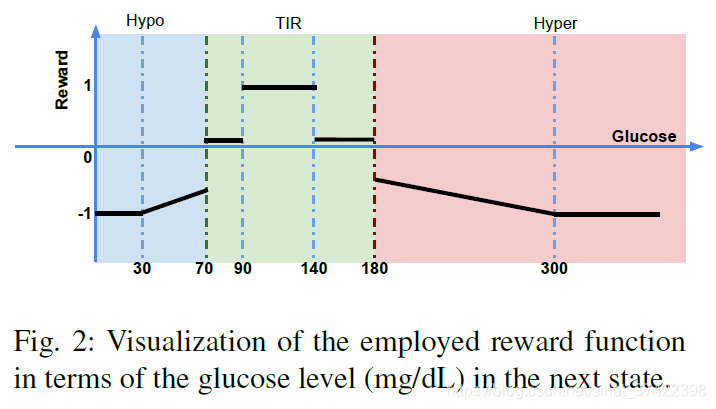
\qquad 在临床试验中，用于训练的数据通常非常有限，因此我们的目标是快速学习性能。因此，我们使用 a double DQN with modified importance sampling 来进一步优化逼近的动作值。一种先进的技术被用来加速学习过程，其中 prioritized experience replay samples important transitions 更常用 [30,31]。 为了避免过高估计动作值，double DQN通过两个独立的神经网络[32] 解耦动作选择和值评估，如图3所示。第二步适用于临床试验环境，模型能够在相对较短的时间内自我调整。

2.3 Generalized DQN Training

\qquad 在第一步中，我们通过使用每个虚拟组（即，成年人和青少年）的平均 T1D subject 利用模拟器生成一个环境。与标准的RNNs相比，DRNNs更适合作为学习 delivery strategies 的DQNs。扩张带来的大感受野可以有效提取葡萄糖时间序列的特征，其中扩张的跳跃连接可以表示为：

\qquad 其中，$c_t^{(l)}$ 是第 $l$ 层在时刻 $t$ 的 cell ，$n_t^{(l)}$ 是时刻 $t$ 第 $l$ 层的输入，$d^{(l)}$ 表示第 $l$ 层的扩张，并且 $f(.)$ 表示 RNN cells 的输出函数。如图3所示，我们使用 三个 有指数级增加的扩张的 DRNN 层，对多维时间对齐序列进行处理，提取高层特征。然后利用仿真器训练 double DQN 的权值 ${\theta }_1,{\theta }_2$ ，其中 动作选择对应 ${\theta }_1$ 、值估计对应 ${\theta }_2$，分别从两个独立的网络获得。根据式（2），action-selection networks 训练时，损失为：

\qquad 其中 $\rho$ 是一个 mini-batch，其中的 transitions $(o,a,r,o^{\prime })$ 是从 memory pool 中的采样，并且
是通过图3中的 action selection DQN 获得。因此，Q-function 可以被更新为:

\qquad 其中 $\alpha$ 是学习率，并且每隔固定的一段时间参数 ${\theta }_1$ 被赋值给 ${\theta }_2$。在每次迭代 [33] 时，采用Adam方法优化学习率。算法1给出了相应的伪码。

对比DDQN（double deep Q-learning）算法流程：

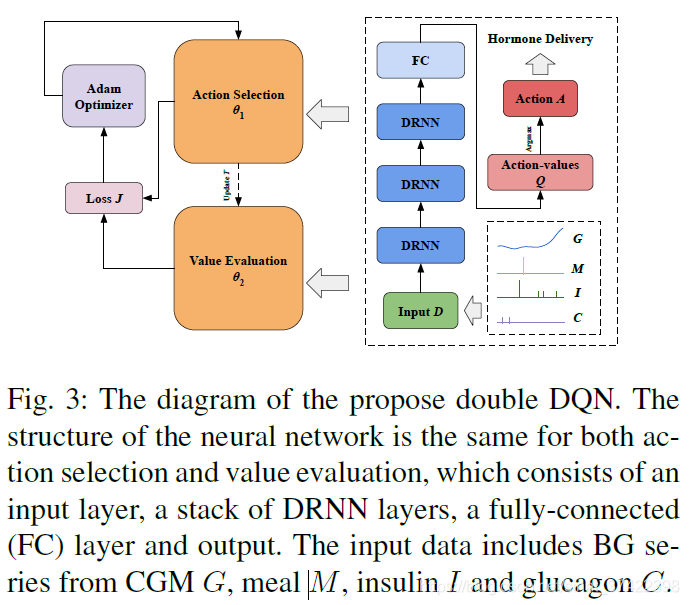
\qquad 对于每一餐，需要注射大剂量胰岛素，agent 使用基于 $Q_{{\theta }_1}$ 的策略 $\pi$ （$\epsilon$-贪心策略）随机地选择胰岛素输注行为。在这种情况下，随机的行动探索具有很大的灵活性并且不需要关注安全问题，正因如此才使用模拟器。注意，在RL过程开始的时候进行一些人工干预可能会减少训练时间，但是在我们的实验中，认为这是不必要的。在这一步的最后，我们可以得到一个权重为 ${\theta }_1$ 和 ${\theta }_2$ 的 a double DQN 的 generalized model。

2.4 Personalized DQN Training

\qquad 在建立了一个 generalized model 之后，我们根据个人特征，通过迁移学习对模型进行了微调。从 generalized model 中提取权重和特征，然后短时间内利用带有安全约束的数据集训练一个个性化的DQNs。我们 可以对 generalized model 所有层进行微调，或者保留一些 earlier layers 的权值，只对网络的 higher-level portion 进行微调，以避免过拟合 。在实验中，我们发现 earlier layers 含有更多的通用特征 (例如低血糖趋势中的胰岛素混悬液)，这对所有T1D受试者都是有用的。
\qquad 这里使用一个从 [31] 修改的方法来计算策略生成的数据的 loss。特别的 $J_n(Q)$ 有一个 $n-stepreturn$ ( n = 12) 来向 earlier states 传送价值 $r_t+{\gamma }_{i+1}+...+{\gamma }^{n-1}{r}_{i+n-1}+ma{x}_{a}Q(o_{i+n},a)$ ， $J_{L_2}(Q)$ 是一个作用于 $\theta$ 的 L2 正则化损失 来防止过拟合。优先级经验回放 根据正比于重要性的 概率 $P_{r_i}$ 对 transitions 进行采样，由以前的数据计算，然后再归一化：

\qquad 其中，$\alpha \in [0,1]$ 决定了使用优先级的水平；$p_i$ 是 transition $i$ 的优先级，根据 last temporal-difference (TD) error ${\delta }_i$ 计算得到；${ϵ}^{\prime }$ 是一个小的正数。他允许 DQN 以比较大的 TD error 更频繁的回放 transitions。此外，为了确保激素在临床试验中安全输注，在执行前对建议的行动采用了限制条件 $\mathcal{C}$。我们使用了一个简单的 安全约束策略：当当前血糖低于80 mg/dL时暂停基础胰岛素，超过160 mg/dL时暂停胰高血糖素。 在实践中，BG水平的趋势和预测也可用于早期干预的安全约束（可以利用对BG水平的预测，提前采取安全措施 ）。通过对广义模型的适当训练和足够的安全约束，该算法可以应用于临床试验。算法2给出了相应的伪代码。

3 Experiments

\qquad 按照图1所示的架构评估设置，我们使用 UVA/Padova T1D 模拟器[27]在 in silico 中进行了实验，以评估所提出的 deep RL 框架的有效性。如 2.1.2 节所述，我们在提出的deep RL (DRL) 算法中使用两种控制动作设置：单激素(DRL- sh)和双激素释放(DRL- dh)。在采用迁移学习策略后，我们开始了使用算法1模拟1500天的长期探索以获得稳定的广义模型，然后，我们使用算法2模拟30天对队列中的每个个体 (即成年人和青少年) 进行个性化训练。由于需要大量的数据，广义模型需要在模拟器中进行训练，而个性化模型训练则有可能在临床环境中进行。 最后，在90天内对个性化模型进行测试。

3.1 Experimental Setup

3.1.1 In Silico environment

\qquad UVA/Padova T1D 模拟器为 agent 探索和学习策略提供了一个交互式环境。我们在饮食方案场景和 T1D模型[34] 的参数中引入了额外的受试者内部变异性（也就是 加入了一个波动范围）。
\qquad 在实验中，我们采用了 一天4餐 的模式（average cases: 7 am (70 g),10 am (30 g), 2 pm (110 g), 9 pm (90 g)），用餐时间（meal-time）变化 $STD=60min$，用餐量（meal-size）的变化 $CV=10\%$。用餐持续时间（meal-duration） 设定为15分钟。碳水化合物用量 的误差估计为 $-30\%\backsim +10\%$，且分布均匀。meal absorption (膳食吸收) 的变化量设置为 $30\%$， carbohydrate （碳水化合物） 的变化量设置为 $10\%$。insulin sensitivity（胰岛素敏感度） ：成年人设置为 $30\%$、青少年设置为 $20\%$，由 scenario function 在自己的配置文件中生成。这些变异值的选择是基于现有的生理学知识，以达到在这些人群中使用标准治疗[35]时常见的血糖结果。
\qquad 我们记录 每一个 subject 的 intra-day 和 intra-person 变化，为了实现公平的对照，对所有的评估方法使用相同的 scenarios，即相同的日常事件和变化时间序列。我们利用10个虚拟成年人和10个虚拟青少年，加上相应的平均受试者，进行 generalized 训练。

3.1.2 Baseline method

\qquad 作为基线方法，我们使用了在传感器增强胰岛素泵中常见的 low-glucose insulin suspension(LGS) （低血糖胰岛素暂停）策略。LGS系统已被证明可以通过暂停基础胰岛素给药[37]来降低低血糖风险。餐前大剂量计算使用标准的 bolus 计算器[28]。

TIR

3.2 Results

\qquad 为了评估所提出算法的性能，并将其与基线方法进行比较，我们选择了diabetes technology community [38]常用的五个标准血糖指标。包括：
percentage time in the glucose target range of [70; 180] mg/dL (TIR),
percentage time below 70 mg/dL (即，低血糖) (Hypo),
percentage time above 180 mg/dL (即，高血糖) (Hyper),
mean BG levels (Mean),
risk index (RI) —— 风险指数
\qquad 结果用平均值和标准差表示 (mean SD).

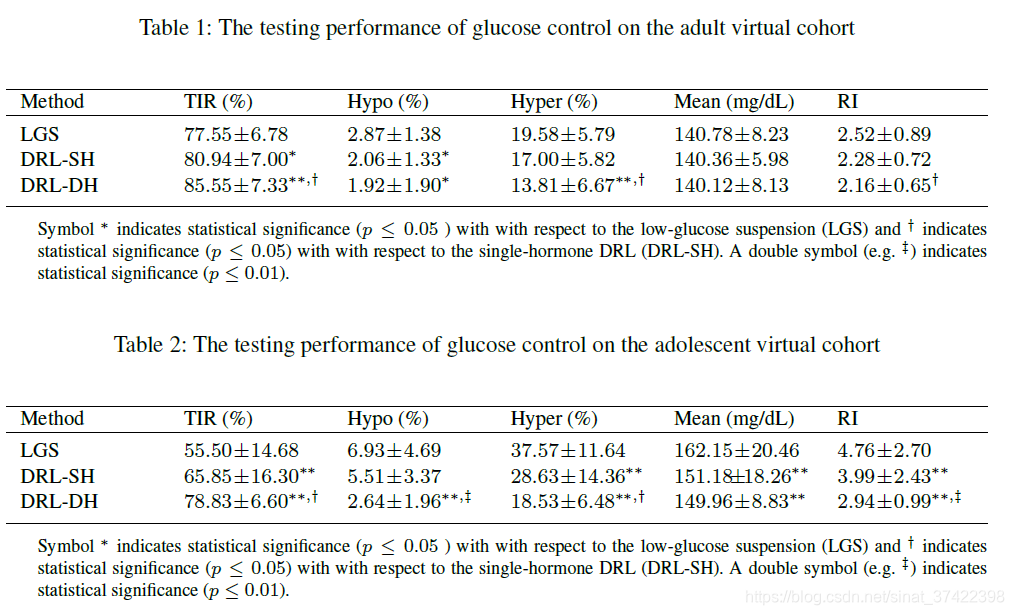
\qquad 表1和表2分别显示了三种测试方法对成人组和青少年组的评价结果。与LGS治疗相比，单激素和双激素DRL模型均通过降低低血糖、高血糖和增加TIR来改善血糖控制性能。值得注意的是，双激素DRL模型显著提高了平均TIR，风险指数显著降低，表现最佳。平均BG水平在成人组保持不变，而在青少年组改善显著。

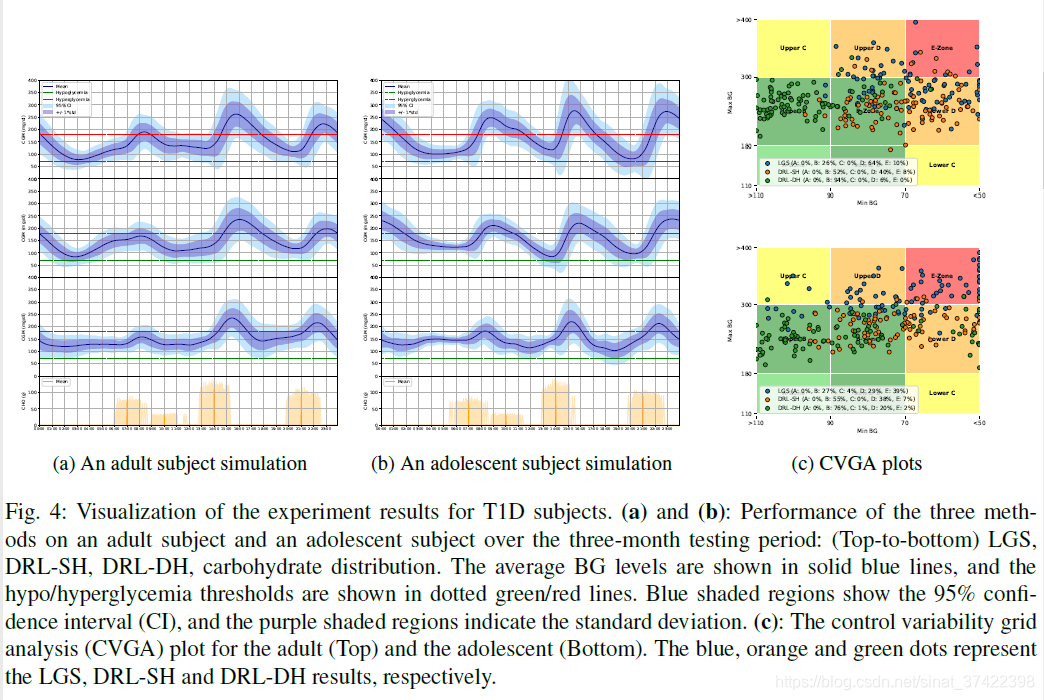
\qquad 为演示目的，图4形象地显示了三种评估方法在三个月的测试期间对所选成年人和所选青少年的性能。特别是24小时内的血糖水平（mean $\pm SD$）（即，动态血糖曲线）、控制变异性网格分析(CVGA)（用于评估闭环胰岛素给药技术的常用工具）。请注意，图4中显示的结果与表1和表2所示的总体人口对应的数值结果是一致的。关于CVGA，值得注意的是DRL-DH与LGS相比取得了显著的改进。特别是，在A+B区，成人组的分数从26%增加到94%，青少年组的分数从27%增加到76%。