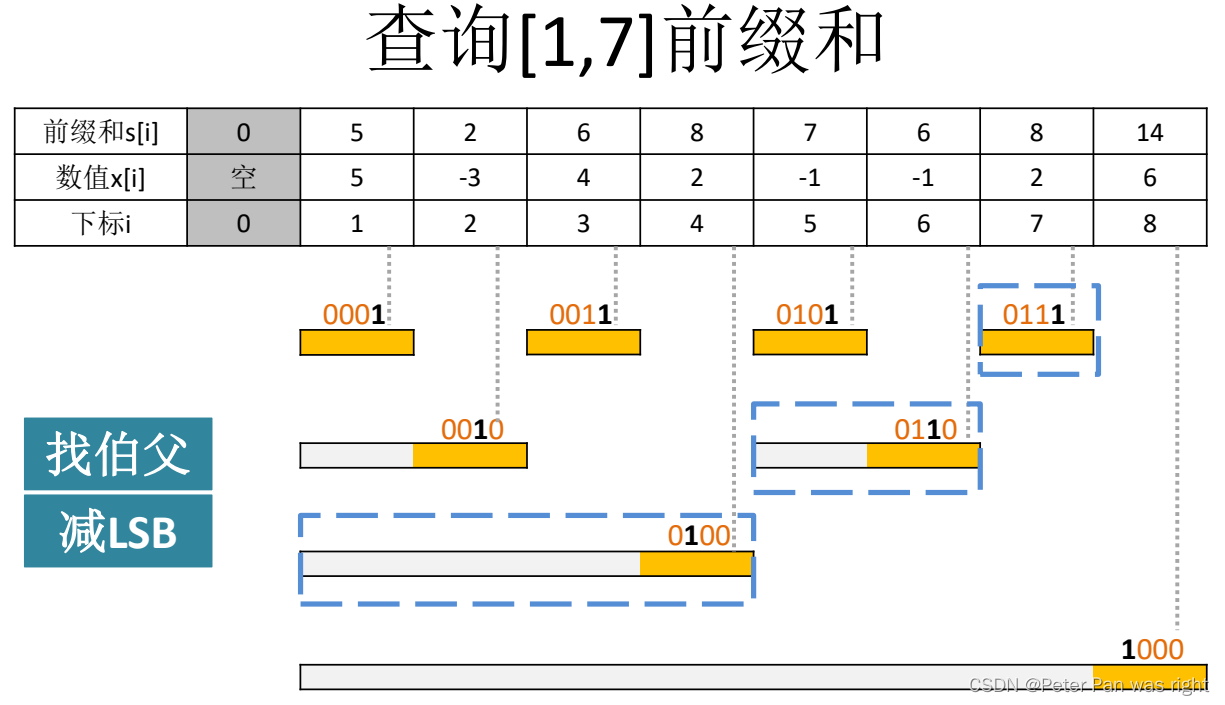
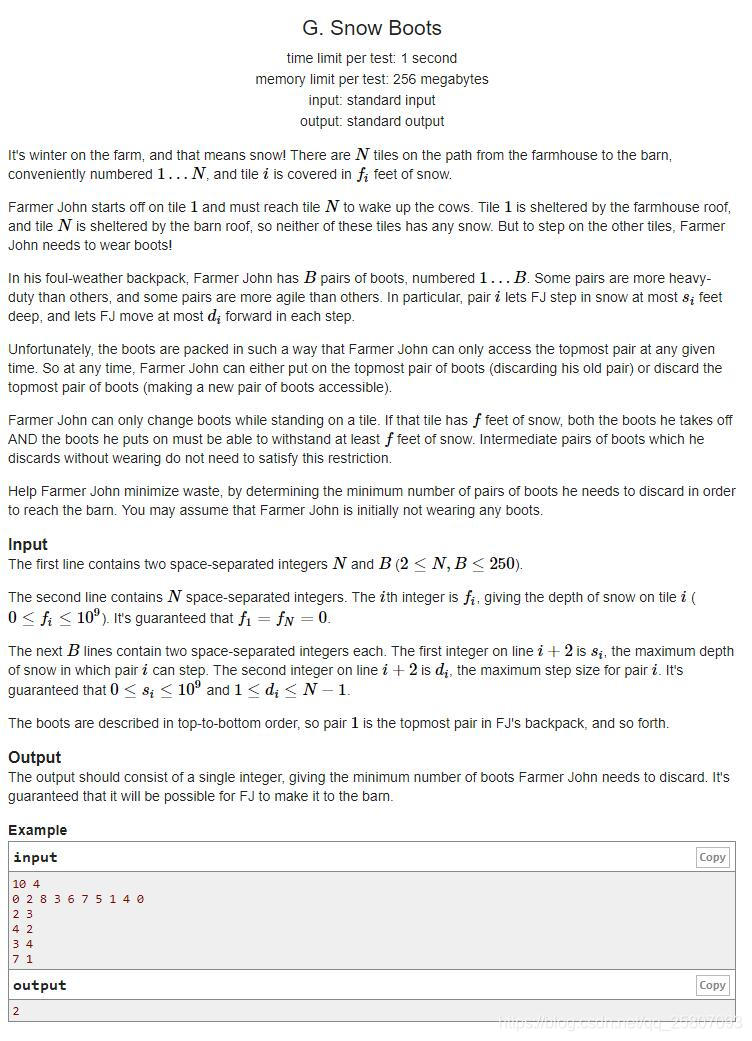
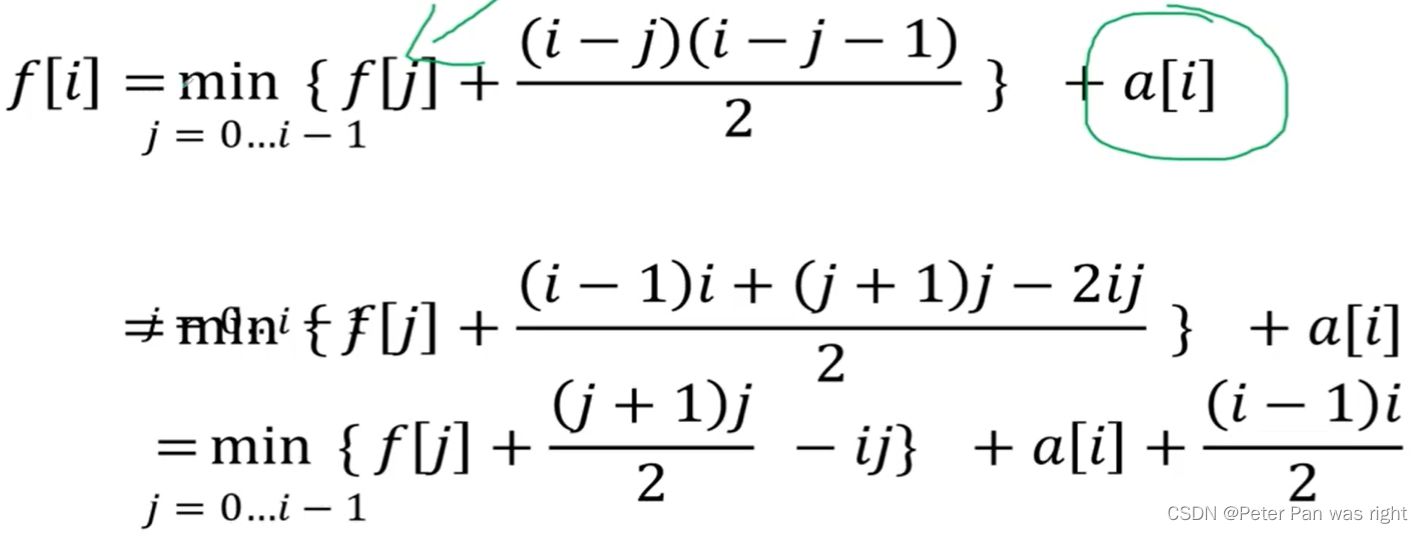上的是汕头市队赛的题面
区别只有数据范围和输出
C 秀恩爱 SRM 06
背景&&描述
KPM坐在直升机上俯瞰小渔村景象。
渔村可看作二维平面，密密麻麻地到处都是单身狗，KPM当前所在坐标为(sx,sy)。
KPM的后宫团们自发地聚集在一起为他送行，从空中看，后宫团形成了一个多边形。
当然了KPM是不在那个多边形内的。
直升机突然开始原地转圈，后宫团们因为想看着KPM的正脸，所以也跟着以KPM所在坐标为中心旋转。
后宫团所经之处单身狗尸横遍野。赶来救治伤员的医护人员想知道，多边形扫过的面积是多少。
注意，本题不保证横坐标互不相同、纵坐标互不相同什么的。
请注意运算过程中可能出现的/0等问题。
输入格式
第一行三个整数，n,sx,sy。n表示多边形的顶点数。
接下来n行每行俩整数，分别表示多边形一个顶点的横纵坐标。
（顶点是按照顺时针或者逆时针顺序给出的，并且所有点的坐标绝对值<=，保证不存在共线的三个顶点）
输出格式
一个整数，表示面积四舍五入为整数的结果。
样例输入
3 0 0 0 1 -1 2 1 2
样例输出
13
数据范围与约定
- 对于100%的数据:
样例解释
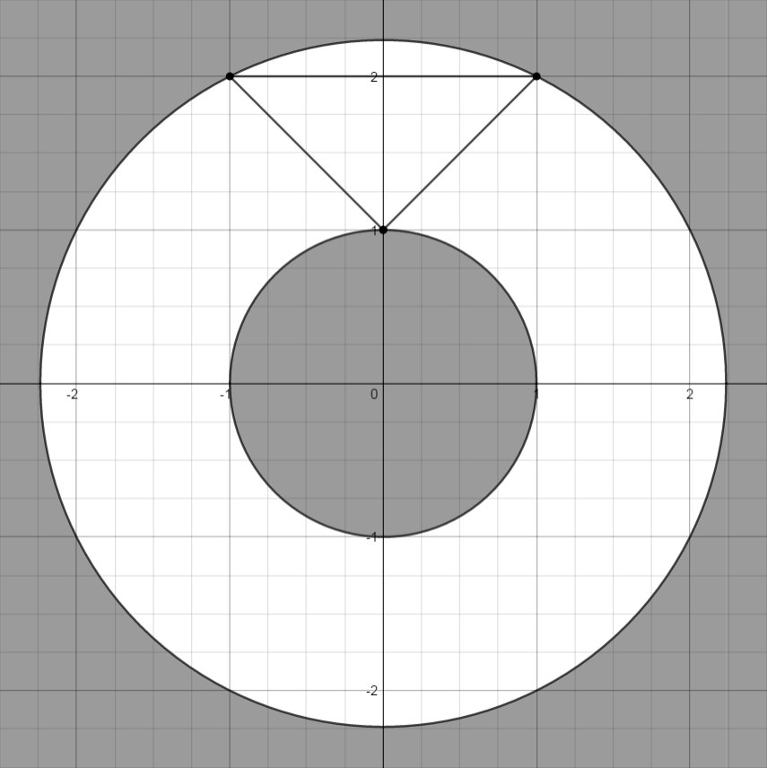
一道想明白就不难的题
但是有很多卡点
很明显发现扫的面积是一个大圆减去小圆
刚开始很容易误以为大圆的半径就是离圆心最远的顶点，小圆的半径就是离圆心最近的
交上去就WA了
刚开始一直想不明白为啥
后来随手造了几组数据就发现了
离圆心最近的点可能不是顶点
而是到边的垂线段的端点
接下来就是数学了
求出那个点到圆心的距离
这个大家可以去学习高中人教版数学必修二（捂脸）
但是一个大坑点：斜率为0！！！
还好我写完随手造了几个数据发现判掉了
这告诉我们写完代码随手造几个小数据手算是一个多么好的习惯
之前一直没有养成
以后一定要这样
然而———我还是WA了
其他人都是没有判除0
我虽然判了但是并没有什么卵用（一脸不爽）
因为我前面算两点距离是爆int了
哇啊啊啊啊啊
多少次爆intWA了啊
怎么就不吸取教训啊
以后看见乘法一定要注意开longlong啊（哭唧唧）
最后还有一个坑点是π的精度
开太低不行
计算器上有
大家可以抄过来
#include<cstdio>
#include<cmath>
const double pie=3.14159265358979323846264338327950288419716939937510,eps=1e-10;
struct node
{int x,y;
}e[100007];
int main()
{int n;long long sx,sy;scanf("%d %lld %lld",&n,&sx,&sy);long long p,q;double min=2*1e14,max=0;int prex,prey;for(int i=1;i<=n;i++){scanf("%lld %lld",&p,&q);e[i].x=p,e[i].y=q;double dis=(p-sx)*(p-sx)+ (q-sy)*(q-sy);if(dis>max) max=dis;if(dis<min) min=dis;}prex=e[n].x;prey=e[n].y;for(int i=1;i<=n;i++){p=e[i].x,q=e[i].y;if(p-prex==0){double tar=p,tary=sy;if(tary-(prey>q?prey:q)<=eps&& tary-(prey<q?prey:q)>=eps ){double dis=(tar-sx)*(tar-sx)+ (tary-sy)*(tary-sy);if(dis<min)min=dis;}}else if(q-prey==0){double tar=sx,tary=q;if(tar-(prex>p?prex:p)<=eps&& tar-(prex<p?prex:p)>=eps ) {double dis=(tar-sx)*(tar-sx)+ (tary-sy)*(tary-sy);if(dis<min) min=dis;}}else{double xie=(q-prey)*1.0/(p-prex);double xie2=-1.0/xie;double b2=(double)sy-xie2*sx;double b1=(double)q-xie*p;double tar=(b2-b1)/(xie-xie2);if(tar-(prex>p?prex:p)<=eps&& tar-(prex<p?prex:p)>=eps ) {double tary=xie2*tar+b2;double dis=(tar-sx)*(tar-sx)+ (tary-sy)*(tary-sy);if(dis<min)min=dis;}}prex=p,prey=q;}double k=pie*(max-min);printf("%.12lf",k);return 0;
}
