变异性的数值特征-方差

文章主要介绍通过样本方差来了解数据集变化的原理。

我们对两个数据集做观察，数据集A和数据集B：

A: 1,2,3,4,5
B: 2,3,3,3,4

对于定量数据集，最常用、也最容易理解的集中趋势测度是数据集的算数平均数。类比我们学生年代，经常谈论的班级平均分。那么，我们对数据集A、B做平均数计算：

A: 3
B: 3

两个样本集的均值都是3。接着，我们计算每个值与均值之间的差值，观察这些偏差数据：

A: (1-3),(2-3),(3-3),(4-3),(5-3)
B: (2-3),(3-3),(3-3),(3-3),(4-3)

从距离的角度，我们在坐标图上做体现。数据集中的每个点跟均值的距离：

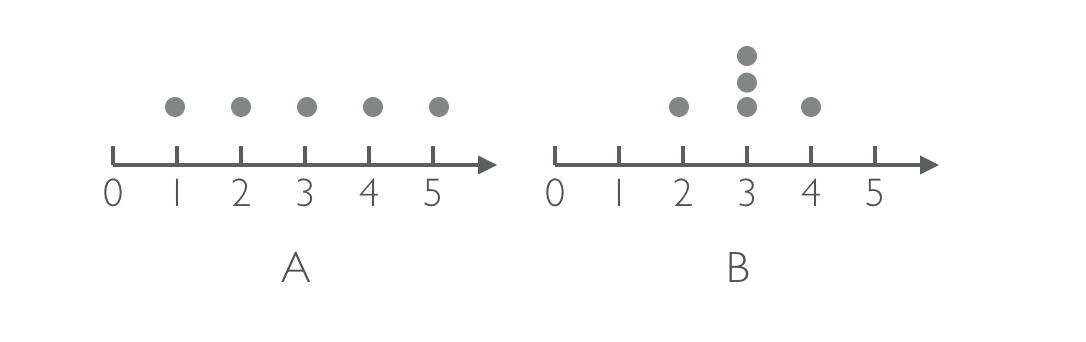
从图上可以看出，数据集A这些点是向外分散的，或者说有较大的变异。数据集B的点都集中在均值3附近，没有太大的变异。

下一步是要将这些有关偏差的信息精简为变异程度的数字度量。距离平均值的偏差有正数，也有负数，取平均值是不可取的。那么，消除偏差的负号的方法就是进行平方处理。

在统计学上，一个含有n个测量值的样本的样本方差等于距离均值的偏差平方和除以(n-1)。

方差的单位是具体单位的平方，我们再对数据做一次处理，计算样本方差的平方根。即标准差。最后，我们通过标准差认为样本值到均值之前的“典型”距离。

在整个过程中，我们通过抽象，最终使用标准差来表示样本的变异性。需要注意的是，计算样本方差的时候，分母是n-1而不是n，主要是因为在使用了n后，会降低总体方差。

参考文章：

1. 商务与经济统计学