Leetcode#42 Trapping Rain Water

原题地址

 

不妨手动模拟一下，观察是否有规律可寻。

假设从位置0开始，我们有一个矩形条

向右扩展，我们遇到了第二个矩形条，假设这个矩形条比第一个矮：

我们继续向右扩展，直到遇到比第一个矩形条高（或者相等）的矩形条：

那么显然，蓝色的部分就是装水的部分，把这部分累加到最终的结果中

然后，以新发现的这个矩形条为左边界，继续向右扩展...

通过模拟我们发现，先固定一个左边界，然后不断向右寻找右边界，哪个是右边界呢？第一个比左边界高（或者相等）的矩形条就是右边界。

这样做显然会有个问题，比如下面这种情况，最右边的矩形条是最后一个矩形条，此时蓝色的部分就不会被算进去，因为最右边的矩形条比红色箭头所指的矩形条矮，它不是右边界。

怎么办呢？倒过来（从右向左）用同样的方式扫一遍就行了。

但是这样还有一个问题，看下面的情况。当左右边界（红色箭头所指）等高时，这部分装水的容量一共会被计算两次（从左向右扫一次，从右向左扫一次）。

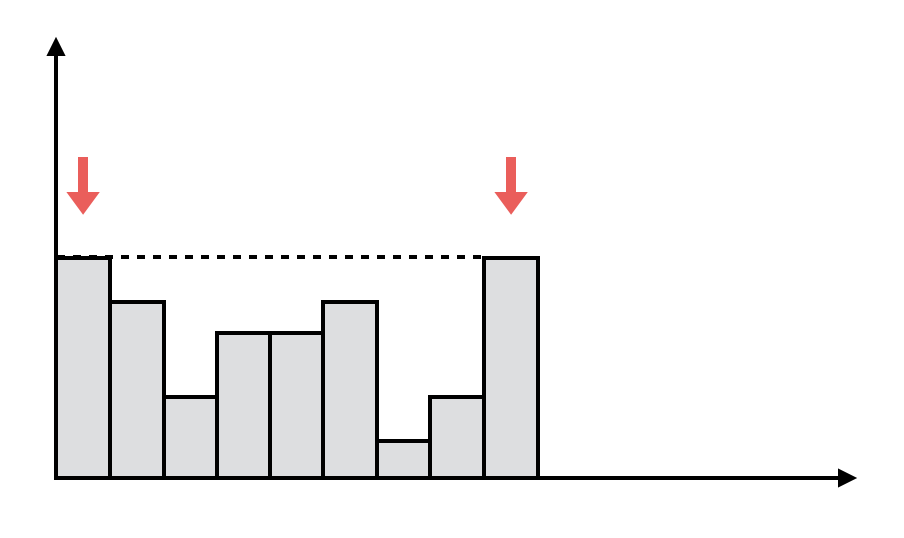
解决方法也很简单，只要规定，从左向右扫的时候左边界一定小于右边界，从右向左扫的时候左边界一定大于等于右边界即可。

 

代码：

int trap(int A[], int n) {
  int sum = 0;
  int acc = 0;
  int i = 0;
  int j = 0;

  // 从左向右扫
  i = 0;
  j = 1;
  acc = 0;
  while (i < n && j < n) {
    if (A[j] < A[i])
      acc += A[i] - A[j];
    if (A[j] > A[i]) {
      sum += acc;
      acc = 0;
      i = j;
    }
    j++;
  }

  // 从右向左扫
  i = n - 1;
  j = n - 2;
  acc = 0;
  while (i >= 0 && j >= 0) {
    if (A[j] < A[i])
      acc += A[i] - A[j];
    else {
      sum += acc;
      acc = 0;
      i = j;
    }
    j--;
  }

  return sum;
}