详解三角面片：实现现实场景的数字化

【版权声明】
本文为博主原创文章，未经博主允许严禁转载，我们会定期进行侵权检索。
更多算法总结请关注我的博客：https://blog.csdn.net/suiyingy，或文末下方”乐乐感知学堂“公众号。
本文章来自于专栏《Python三维模型处理基础》的系列文章，专栏地址为：https://blog.csdn.net/suiyingy/category_12462636.html。  

        在计算机图形学和几何学领域，三角面片是一种重要的基本元素。无论是用于模拟三维物体、渲染场景还是进行几何形状分析，三角面片都扮演着不可或缺的角色。本文将介绍三角面片的概念、应用以及其重要性，带您深入理解这个实现现实场景数字化的基石。

1. 三角面片

        三角面片是由三个顶点和三条边构成的二维几何图形。每条边连接两个顶点，最终形成一个闭合的三角形。三角面片通常被用来描述三维物体的表面，通过大量相邻的三角面片组合而成，可以构建出复杂的形状。
        在三维点云中，很多表面重建的方法的基本原理是通过三角剖分的方法来重建物体表面的三角面。相关介绍内容可参考”https://blog.csdn.net/suiyingy/article/details/124448313“和”https://blog.csdn.net/suiyingy/article/details/124539257“。
        下图分别是一个球面和立方体表面的三角化。从图中可以看到，物体的表面可以划分成若干个三角面。图片对应的Python示例程序下载地址为“https://download.csdn.net/download/suiyingy/88409947”，或者在”乐乐感知学堂“內回复”3d处理基础“即可。

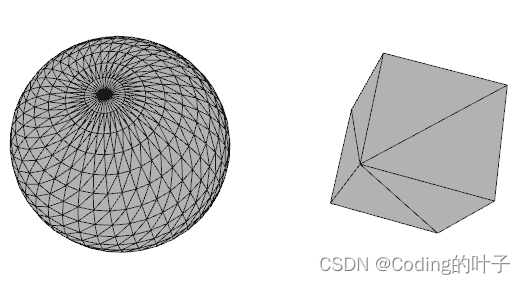
图1 球面和立方体表面三角化示意图

2. 三角面性质

2.1 无序性

        物体表面通常可以用轮廓来进行表示，但这种方法对轮廓顶点的顺序有严格要求。例如，下图有一个四边形轮廓，四个顶点分别为A、B、C、D。当这4个顶点的相对顺序保持不变时，轮廓表面是由AB、BC、CD和DA四条边围成的区域。但是，如果我们将顶点的顺序调整为A、C、B、D，那么会得到一个完全不一样的表面形状，如下图所示。

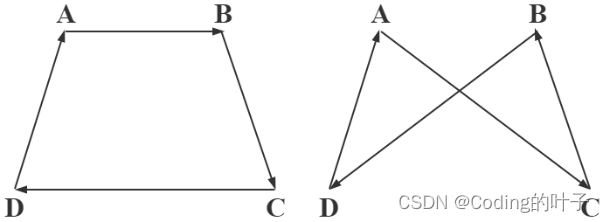
图2 四边形轮廓与顶点顺序

        相比而言，三个顶点组成的平面区域，无论顶点顺序如何变化，所围成的区域都是不变的。另一方面，根据三角剖分等相关数学原理，物体表面可划分成一些列三角面。这些三角面通常也称为网格（mesh）。以obj或ply点云格式为例，这类文件种可分别存储顶点和三角面，顶点由坐标及其属性值构成，而三角面则由顶点序号组成。以一个三棱柱为例，假设三棱柱的6个顶点坐标分别为（0.0， 0.0， 0.0）-1号顶点、（3.0，0.0，0.0）-2号顶点、（0.0，4.0，0.0）-3号顶点、（0.0， 0.0， 5.0）-4号顶点、（3.0，0.0，5.0）-5号顶点、（0.0，4.0，5.0）-6号顶点，形状如下图所示。

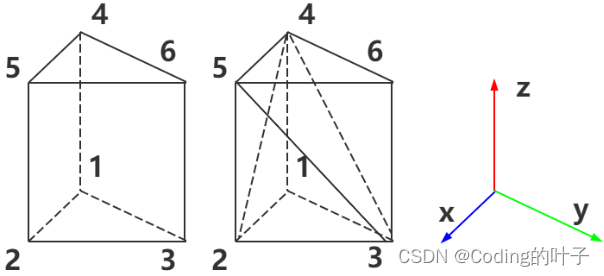
图3 三棱柱及其三角化示意图

        上图中三棱柱的三角面数量为8，上下底面各一个，3个侧面各两个。同一个表面可以有不同的三角面划分方法。例如，一个三角面又可以划分成多个三角面。三棱柱侧面的三角面也可以用不同的对角线进行划分。图中8个三角面的顶点构成分别为（1，3，2）、（2，3，5）、（5，3，6）、（1，4，3）、（3，4，6）、（1，2，4）、（2，5，4）、（4，5，6）。那么，该三棱柱可以使用下面的方式进行存储，其中v表示顶点，f表示三角面。

v 0.0 0.0 0.0
v 3.0 0.0 0.0
v 0.0 4.0 0.0
v 0.0 0.0 5.0
v 3.0 0.0 5.0
v 0.0 4.0 5.0
f 1 3 2
f 2 3 5
f 5 3 6
f 1 4 3
f 3 4 6
f 1 2 4
f 2 5 4
f 4 5 6

        将上述内容保存为以.obj为后缀的文件中即可得到模型文件，可使Windows自带的3D 查看器、CloudCompare、MeshLab等软件直接打开，下图是采用3D 查看器打开的结果。由于3D查看器软件的视角方向和坐标系方向的设置不同，其看到的区域与图3中会有差异。本专栏后续文章会详细介绍相机姿态和视角设置，并获取不同视角的投影图。

图4 3D查看器显示结果

        下图是采用python open3d库显示的结果。open3d和trimesh对应的Python示例程序下载地址为”https://download.csdn.net/download/suiyingy/88409947“，或者在”乐乐感知学堂“內回复”3d处理基础“即可。

图4 open3d程序显示结果

2.2 方向性

        虽然三角面区域与顶点顺序无关，但是其正反面与顺序直接相关。通常情况下，法向量方向满足右手定则，即四指弯曲方向为顶点顺序方向，大拇指所指方向即为法向量方向。
法向量朝外表示该面是正面，否则为反面。从另外一个角度来看，我们观察角度正好是法向量的反方向，即正对正面。一般情况下，逆时针顺序的三角面为正面，但也不绝对，需要根据具体情况和右手定则来决定顶点顺序。

        三角面的方向性在三维模型显示中至关重要。很多三维模型显示软件或者可视化库仅能够显示出正面，并且反面多为全黑，open3d则默认不显示背面。三维模型的各种显示方法相关内容可参考《python点云可视化_python 点云可视化-CSDN博客》、《python open3d点云可视化（本节会根据实际所用持续更新）_open3d可视化点云_Coding的叶子的博客-CSDN博客》。以上述三棱为例，下面第一个图的三角面顶点顺序分别为[[1, 3, 2], [2, 3, 5], [5, 3, 6], [1, 4, 3], [3, 4, 6], [1, 2, 4], [2, 5, 4], [4, 5, 6]]，所有面的法向量均朝外。第二个图的三角面顶点顺序分别为[[1, 2, 3], [2, 3, 5], [5, 3, 6], [1, 4, 3], [3, 4, 6], [1, 2, 4], [2, 5, 4], [4, 5, 6]]，改变第一个底面三角面的顶点顺序。第三个图的三角面顶点顺序分别为[[1, 2, 3], [3, 2, 5], [5, 3, 6], [1, 3, 4], [3, 4, 6], [1, 2, 4], [2, 5, 4], [4, 5, 6]]，改变第一个底面三角面、第1个侧面和第3个侧面的顶点顺序。

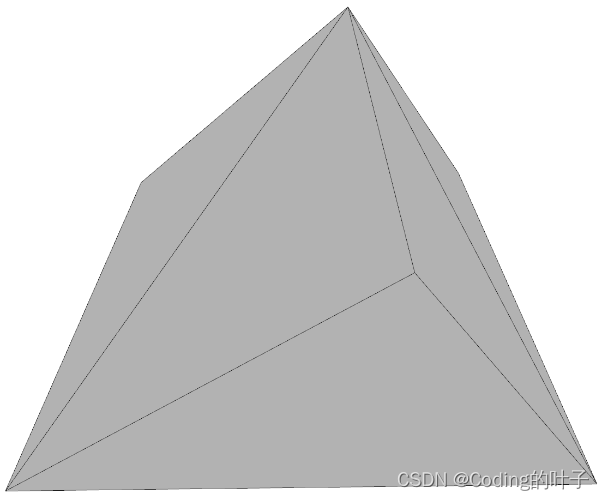
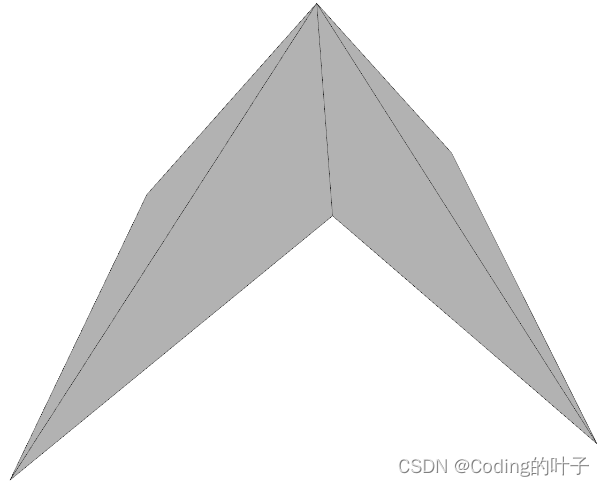
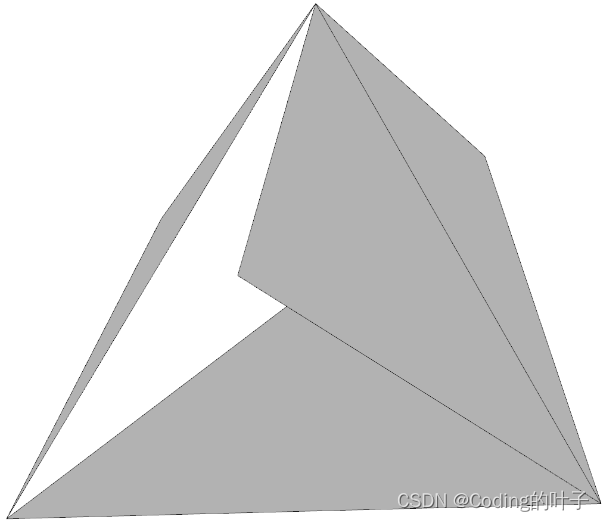
图5 三种不同顶点顺序下open3d显示结果

        三角面方向性的另一个重要影响是三维模型的体积计算，会严重影响结果的准确性。这个我们将在下一篇博文中详细进行介绍。

3. 示例程序

        处理三角面的常用python库有open3d和trimesh，并且open3d.geometry.TriangleMesh对象和trimesh.Trimesh对象可以互相转换。示例程序下载地址为”https://download.csdn.net/download/suiyingy/88409947“，或者在”乐乐感知学堂“內回复”3d处理基础“即可。

mesh = trimesh.Trimesh(vertices=vertices, faces=faces)
# 转换为open3d的o3d.geometry.TriangleMesh对象
mesh1 = mesh.as_open3d
# 将 Open3D 中的 TriangleMesh 对象转换为 Trimesh 类型对象
vertices = np.asarray(mesh1.vertices)
faces = np.asarray(mesh1.triangles)
mesh2 = trimesh.Trimesh(vertices=vertices, faces=faces)

4. 模型动画

        下面是本文三棱柱模型对应的gif动画，模型动画制作方法会在后续博文进行详细介绍。

图6 模型动画

5. 三角面片的应用领域

        （1）计算机图形学：在计算机图形学中，三角面片是渲染三维场景的基础单元。通过为每个三角形分配颜色、纹理和法线，可以创建逼真的三维效果。此外，三角面片也广泛应用于三维建模和动画制作领域。

        （2）虚拟现实和增强现实：在虚拟现实和增强现实应用中，三角面片被用来构建虚拟环境和虚拟物体。通过合理安排三角面片的位置和形状，可以实现逼真的虚拟场景，并提供身临其境的用户体验。

        （3）计算机辅助设计：在CAD软件和工程领域，三角面片常用于表示三维模型的几何信息，帮助工程师进行设计分析和可视化展示。

6. 三角面片重要性

        （1）可计算性：由于三角面片的几何性质简单明确，对其进行计算和处理相对容易。这使得三角面片成为计算机图形学和几何学中常用的表示方法。

        （2）高效性：三角面片具有紧密的结构，相邻面片之间共享边界，从而有效地减少了存储和计算的开销。这种高效性使得三角面片在处理大规模三维数据时表现出色。

        （3）灵活性：通过调整顶点坐标和连接顺序，可以改变三角面片的形状，从而实现各种复杂对象的建模和变换。这种灵活性使得三角面片成为三维形状的理想选择。

        作为计算机图形学和几何学中的重要概念，三角面片在现实世界的模拟和可视化中发挥着不可或缺的作用。无论是在虚拟场景的构建、产品设计的优化还是工程分析的展示上，三角面片都为我们带来了前所未有的便利和效果。希望通过本文的介绍，您对三角面片有了更深入的了解，并能够在相关领域中灵活应用。

【版权声明】
本文为博主原创文章，未经博主允许严禁转载，我们会定期进行侵权检索。
更多算法总结请关注我的博客：https://blog.csdn.net/suiyingy，或文末下方”乐乐感知学堂“公众号。
本文章来自于专栏《Python三维模型处理基础》的系列文章，专栏地址为：https://blog.csdn.net/suiyingy/category_12462636.html。