CF505B Mr. Kitayuta‘s Colorful Graph

本文主要是介绍CF505B Mr. Kitayuta‘s Colorful Graph，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Mr. Kitayuta’s Colorful Graph

题面翻译

给出一个 $n$ 个点，$m$ 条边的无向图，每条边上是有颜色的。有 $q$ 组询问

对于第 $i$ 组询问，给出点对 $u_i,v_i$。求有多少种颜色 $c$ 满足：有至少一条 $u_i$ 到 $v_i$ 路径，满足该路径上的所有边的颜色都为 $c$

输入格式

第一行两个整数 $n,m$ 分别表示点的个数和边的个数
接下来 $m$ 行，每行三个整数 $x_i,y_i,c_i$，表示有一条连接点 $x_i,y_i$ 的边，且该边的颜色为 $c_i$

接下来一行一个整数 $q$，表示询问的个数

接下来 $q$ 行，每行两个整数 $u_i,v_i$，表示一组询问

输出格式

对于每一组询问，在单独的一行输出一个整数，表示满足上述要求的颜色种数

说明与提示

$2\le n\le 100$
$1\le m,q\le 100$
$1\le x_i,y_i,u_i,v_i\le n$
$1\le c_i\le m$
感谢 @_Wolverine 提供的翻译

题目描述

Mr. Kitayuta has just bought an undirected graph consisting of $ n $ vertices and $ m $ edges. The vertices of the graph are numbered from 1 to $ n $ . Each edge, namely edge $ i $ , has a color $ c_{i} $ , connecting vertex $ a_{i} $ and $ b_{i} $ .

Mr. Kitayuta wants you to process the following $ q $ queries.

In the $ i $ -th query, he gives you two integers — $ u_{i} $ and $ v_{i} $ .

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex $ u_{i} $ and vertex $ v_{i} $ directly or indirectly.

输入格式

The first line of the input contains space-separated two integers — $ n $ and $ m $ ( $ 2<=n<=100,1<=m<=100 $ ), denoting the number of the vertices and the number of the edges, respectively.

The next $ m $ lines contain space-separated three integers — $ a_{i} $ , $ b_{i} $ ( $ 1<=a_{i}<b_{i}<=n $ ) and $ c_{i} $ ( $ 1<=c_{i}<=m $ ). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if $ i≠j $ , $ (a_{i},b_{i},c_{i})≠(a_{j},b_{j},c_{j}) $ .

The next line contains a integer — $ q $ ( $ 1<=q<=100 $ ), denoting the number of the queries.

Then follows $ q $ lines, containing space-separated two integers — $ u_{i} $ and $ v_{i} $ ( $ 1<=u_{i},v_{i}<=n $ ). It is guaranteed that $ u_{i}≠v_{i} $ .

输出格式

For each query, print the answer in a separate line.

样例 #1

样例输入 #1

4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4

样例输出 #1

2
1
0

样例 #2

样例输入 #2

5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4

样例输出 #2

1
1
1
1
2

提示

Let’s consider the first sample.

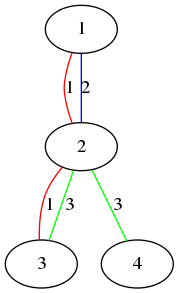The figure above shows the first sample. - Vertex $ 1 $ and vertex $ 2 $ are connected by color $ 1 $ and $ 2 $ .

• Vertex $ 3 $ and vertex $ 4 $ are connected by color $ 3 $ .
• Vertex $ 1 $ and vertex $ 4 $ are not connected by any single color.

思路

（1）并查集
一个二维并查集，一个记录颜色，一个记录点。
（2）Floyed
普通Floyed加一维颜色。数据只有100四维循环不会T。

AC code

（1）并查集

#include<bits/stdc++.h>using namespace std;int fa[1000][1000];
int n, m, t;int find(int x, int i) 
{if (fa[x][i] == x) return x;return fa[x][i] = find(fa[x][i], i); 
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)fa[i][j] = i; for (int i = 1; i <= m; ++i){int u, v, z;cin >> u >> v >> z;fa[find(u, z)][z] = find(v,z); }cin >> t;while (t--){int u, v, ans = 0;cin >> u >> v;for(int i = 1; i <= m;i++)if (find(u,i) == find(v,i)) ans++; cout << ans << endl;}return 0;
}

（2）Floyed

#include<bits/stdc++.h>using namespace std;int a[101][101][101];int main()
{int n, m;cin >> n >> m;for(int i = 1; i <= m; i++){int u, v, q;cin >> u >> v >> q;a[u][v][q] = 1;a[v][u][q] = 1;}for (int k = 1; k <= n; k++)for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)for (int c = 1; c <= m; c++)if (a[i][k][c] == 1 && a[k][j][c] == 1)a[i][j][c] = 1;int q;cin >> q;for (int i = 1; i <= q; i++){int u, v;cin >> u >> v;int sum = 0;for(int j = 1; j <= m; j++)if(a[u][v][j] == 1)sum++;cout << sum << endl;}return 0;
}

这篇关于CF505B Mr. Kitayuta‘s Colorful Graph的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---