本文主要是介绍挑战运筹学——敏感度分析及对偶性,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
影子价格
将问题用数学形式完整地表达
- LP问题的一般形式
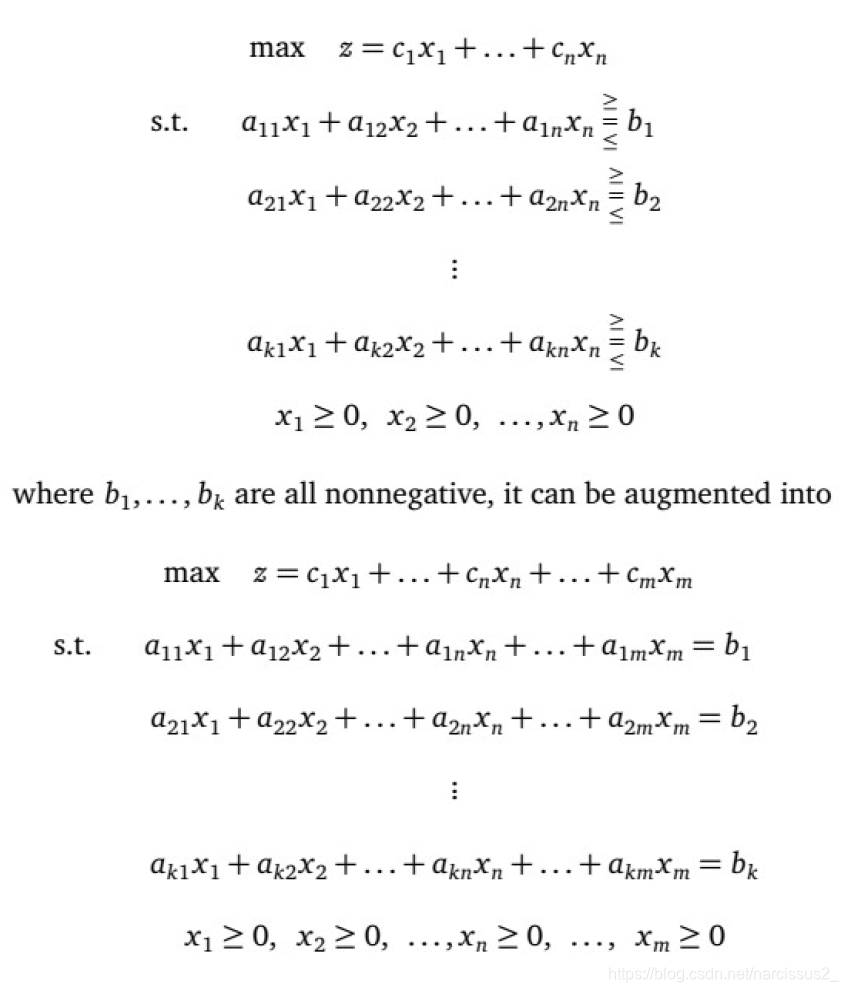
将数学符号简化

- 我们将会学习在优化问题中改变 A 0 , C 0 o r B A_0, C_0 or B A0,C0orB会导致什么。
- 在很多情况中,constraint同样会变化,所以有关限制的研究也是要考虑的。
考虑一个案例

- x 1 x_1 x1是每周生产士兵玩具的数量。
- x 2 x_2 x2是每周生产火车的玩具数量。
- 三个限制分别是加工,雕刻和需求的限制。
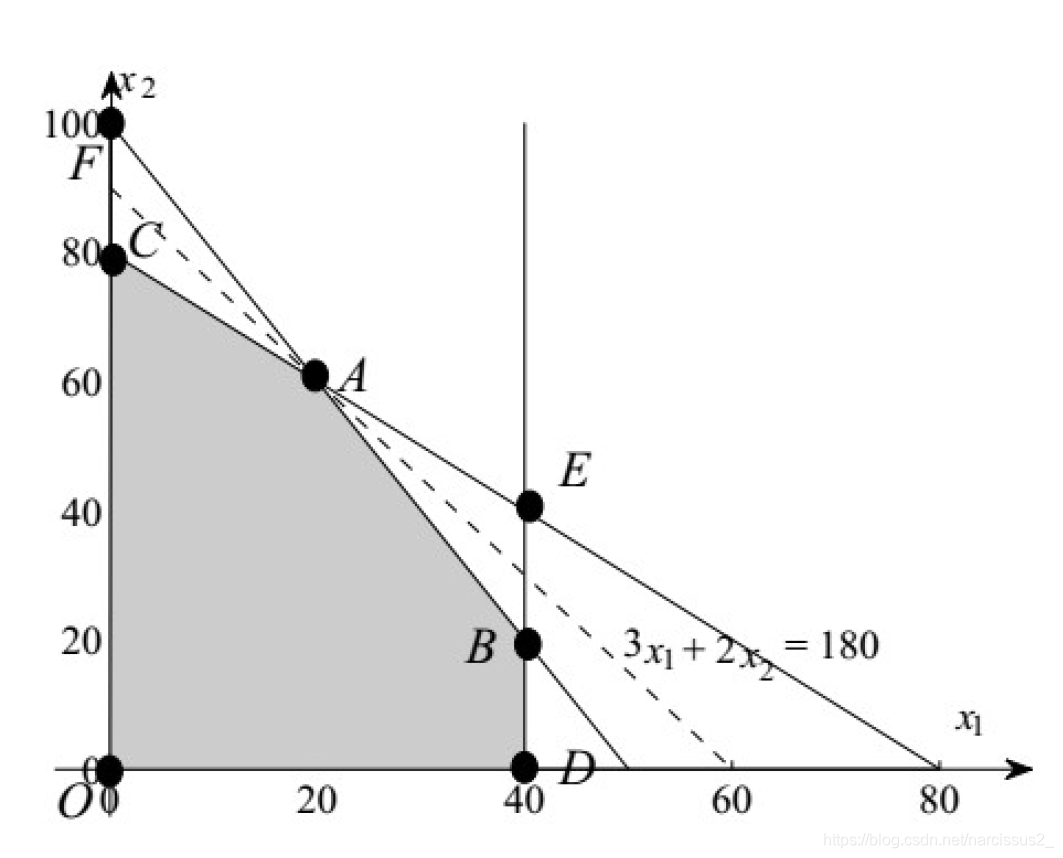
关于 C 0 C_0 C0的变化
- 在这个案例中,可行域保持不变。随着 C 0 C_0 C0的变化,目标函数轮廓的梯度也会发生变化。
- 考虑目标函数为 z = ( 3 + ϕ ) x 1 + 2 x 2 z = (3+\phi )x_1+2x_2 z=(3+ϕ)x1+2x2
- 在 A = ( 20 , 60 ) , z = ( 3 + ϕ ) ( 20 ) + 2 ( 60 ) = 180 + 20 ϕ A=(20,60), z = (3+\phi )(20)+2(60)=180+20\phi A=(20,60),z=(3+ϕ)(20)+2(60)=180+20ϕ
- 当 ϕ \phi ϕ增加的时候,目标函数会越来越陡峭,直至与线AB完全平行·,此时 ϕ \phi ϕ的值为。

- 当 ϕ > 1 \phi>1 ϕ>1,最优点移动到B,且Z的表达式为

- 而当 ϕ \phi ϕ减小的时候,最优点会保持在A直至 ϕ = − 1 \phi = -1 ϕ=−1

- 此时线段平行于AC,最优点可以出现在AC上的任意一点。
- 当 ϕ < − 1 \phi<-1 ϕ<−1,最优点从AC移动到C,Z的表达式为。

关于B的变化
- 在这种情况下,可行域的边界是平行移动的。因此可行区域的角点是移动的,但是当目标函数的梯度保持不变时,最优点仍保持在同一个(移动)角上,直到几何变化使两个角重合为止。
- 在 c i c_i ci后面添加 Δ \Delta Δ是很容易理解的,就是将线段平行移动,这里就不做多的解释。
影子价格
- 我们知道管理人员要做的一件重要的事情常常是确定约束条件右端项的变化如何改变LP的最优z值。
- 所以,我们把LP的i个约束条件的影子价格定义为第i个约束条件的右端项增加1时,最优z值改善的量。
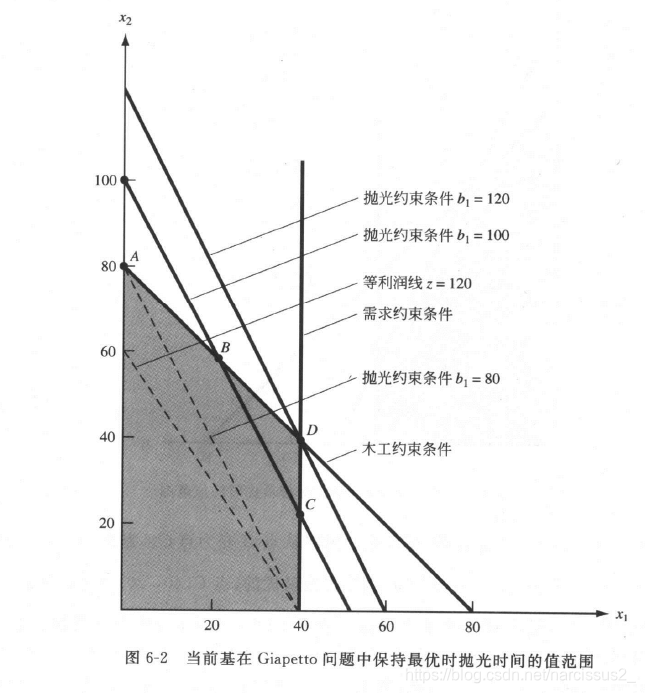
例题1
- 找到第二个限制的影子价格
- 解决方案: 对于第二项约束(carpentry hour),我们知道如果80 个木工小时,而当前的解是最优的,那么对于LP问题的优化解是 x 1 = 20 − Δ x_1=20-\Delta x1=20−Δ和 x 2 = 60 + 2 Δ x_2=60+2\Delta x2=60+2Δ。最优的z值shi 3 x 1 + 2 x 2 = 3 ( 20 − Δ ) + 2 ( 60 + Δ ) = 180 + Δ 3x_1+2x_2=3(20-\Delta)+2(60+\Delta)=180+\Delta 3x1+2x2=3(20−Δ)+2(60+Δ)=180+Δ
- 所以只要当前基保持最优,可用抛光时间增加一个单位将使最优z值增加1美元。因此,第一个(抛光时间)的约束条件的影子价格是1美元。
例题2
- (a) 找到下列问题的解

- 易得
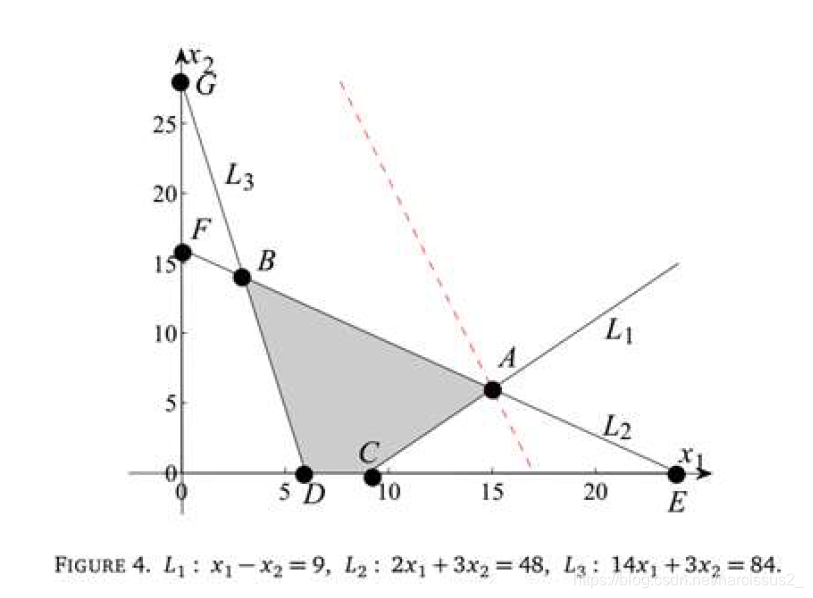
- 结果为 x 1 = 15 , x 2 = 6 , z = 51 x_1=15, x_2 = 6, z = 51 x1=15,x2=6,z=51
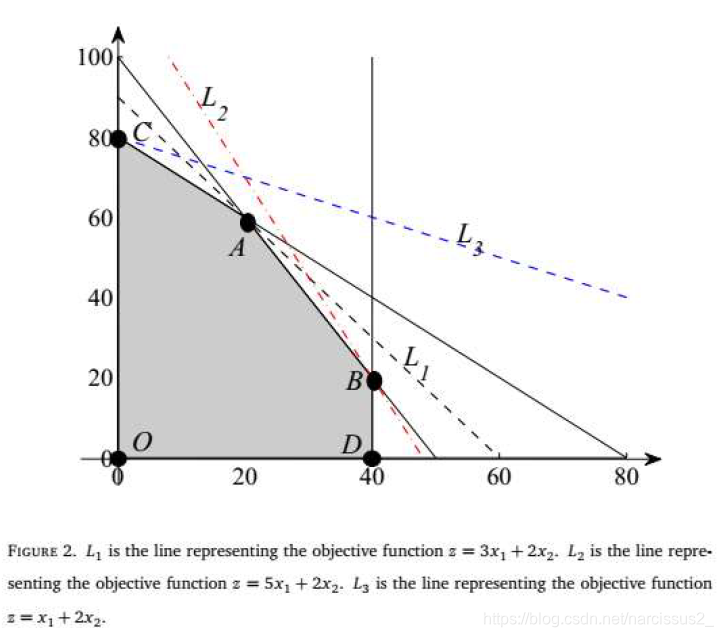
(b) 如果目标函数 x 2 x_2 x2的系数被替换成了 1 + ϕ 1+\phi 1+ϕ, ϕ \phi ϕ的范围,使得最优结果不改变。当 ϕ \phi ϕ超过上限时,新的可行域是什么。
答:由题可知,新的目标函数为 3 x 1 + ( 1 + ϕ ) x 2 3x_1+(1+\phi)x_2 3x1+(1+ϕ)x2,梯度为:
− 3 1 + ϕ -\frac{3}{1+\phi} −1+ϕ3
为了当前解保持最优,梯度L必须在 L 1 L_1 L1和 L 2 L_2 L2之间,它们的梯度分别是1和 − 2 3 -\frac{2}{3} −32


所以 ϕ \phi ϕ的范围是 − 4 ≤ ϕ ≤ 3.5 -4\leq \phi \leq 3.5 −4≤ϕ≤3.5
当 ϕ \phi ϕ>3.5的时候,斜率应该是小于- 2 3 \frac{2}{3} 32,所以应该是过B点

重要公式
- LP可以写作

- 把Dakota问题写作

- 假设我们已经求出了(1)的最优解,设 B V i BV_i BVi,是最优表第i行的基变量。此外定义 B V = { B V 1 , B V 2 , . . . , B V m } BV = \{BV_1, BV_2,..., BV_m\} BV={BV1,BV2,...,BVm}是最优表中基变量的集合,并定义m×1向量

- NBV则为非基变量的集合
- X N B V X_{NBV} XNBV为按照需要的顺序列出非基变量(n-m)*1向量



LP问题的数学符号

- 然后我们尝试用 B − 1 B^{-1} B−1和第一条约束相乘,得到

- 对于Dakota问题,可以使用高斯-约当方法得到 B − 1 B^{-1} B−1为

- 由此可以得到





公式小结

- 其实无非就是看公式,做题然后找感觉。
敏感度分析
- 我们现在研究改变LP问题额的参数如何改变最优解。
- 对于LP的最优解与其参数的关系的分析称为灵敏度分析。
- 再回到之前Dakota问题的案例。

LP参数的6种变化
- 变化1:改变非基变量的目标函数系数。
- 变化2:改变基变量的目标函数系数
- 变化3:改变约束条件的右端项。
- 变化4:改变非基变量的列。
- 变化5:增加新的变量或活动
- 变化6:增加新的约束条件(见6.11节)
变化1:改变非基变量的目标系数
- 在Dakota问题中,唯一的非基本决策变量是 x 2 x_2 x2(餐桌)。 x 2 x_2 x2的目标函数系数目前是 C 2 = 30 C_2 = 30 C2=30。 c 2 c_2 c2的变化将如何影响Dakota问题的最优解呢?更确切地讲 c 2 c_2 c2应该取什么能保证 B V = { s 1 , x 3 , x 1 } BV = \{s_1,x_3,x_1\} BV={s1,x3,x1}保持最优呢?
- 首先我们将 c 2 c_2 c2从30改成 30 + Δ 30+\Delta 30+Δ时将如何改变BV表。注意, B − 1 B^{-1} B−1和b没有变化,所以 ( B − 1 b ) (B^{-1}b) (B−1b)没有被改变,因此BV仍然是可行的。
- 由于 x 2 x_2 x2是非基变量,所以 c B V c_{BV} cBV没有被改变。由(10)可知, c 2 c_2 c2的变化将改变其第0行系数的。
- 由(10)可知, c 2 c_2 c2的变化将改变其第0行系数的唯一变量是 x 2 x_2 x2
其他的对照公式也算是大同小异
特别案例

- 问:如何快速求得 B − 1 B^{-1} B−1
- 答:观察可知Initial tableau中 s 1 , a 2 , a 3 s_1, a_2, a_3 s1,a2,a3构成了0-1矩阵,Final中0-1矩阵转移,剩下的 s 1 , a 2 , a 3 s_1,a_2,a_3 s1,a2,a3求出的就是 B − 1 B^{-1} B−1。
求LP的对偶
- 与一个LP有关的另一个LP称为对偶。知道LP及其对偶之间的关系对于理解线性和非线性规划的高级内容。
- 在求给定LP的对偶时,我们把给定的LP称为原问题(primal)。如果原问题是max问题,那么其对偶问题就是min问题。
- 我们首先解释如何求其中所有变量都必须是非负数,并且所有约束都必须是≤约束条件的max问题(称为normal max problem)
- 一个规范max问题
- 一个这样的规范max问题的对偶被定义为
 * 像17这样约束条件都是≥,并且所有变量都是非负数的min问题称为规范min问题。
* 像17这样约束条件都是≥,并且所有变量都是非负数的min问题称为规范min问题。
获得规范max问题和规范min问题的对偶
- 其实这个看着找规律即可
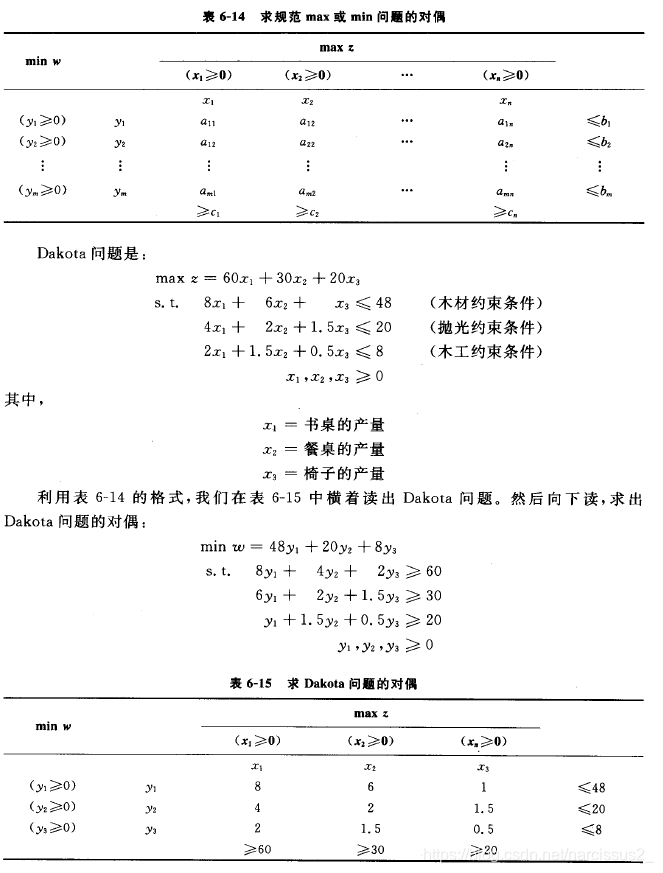
非规范对偶性

usr代表unrestricted-in-sign变量,为无符号限制变量.
解决步骤
- 第1步:填写表格,使得可以横着读出。
- 第2步:通过以下方式读出对偶:
a. 如果第i个原约束条件是≥约束条件,那么对应的对偶变量 y i y_i yi必须满足 y i ≤ 0 y_i\leq 0 yi≤0
b. 如果第i个原约束条件是等式的约束条件,那么对应的对偶变量 y i y_i yi将会是符号无限制变量。
c. 如果第i个原变量是urs,那么第i个对偶约束条件将是等式约束条件。


对偶性定理
- 假设BV是Primal的最优基 ,那么 C B V B − 1 C_{BV}B^{-1} CBVB−1是一个对偶性问题的最优解。
- 直接套公式!
对偶性及敏感性分析
- 如果BV第0行保持非负,那么BV将保持最优。由于原始最优性和对偶可行性都是等价的,因此可以看到,当且仅当当前对偶解 c b v B − 1 c_{bv}B^{-1} cbvB−1保持对偶可行时,上述变化将使当前基最优。
原

DUAL

如果改变 y 2 y_2 y2的系数
- 那么DUAL对应的会这么改变

- 将原先的解(0,10,10)带进来, c 2 c_2 c2最大为35。
- 所以 c 2 < 35 c_2<35 c2<35,它将会一直保持最优。
互补松弛性
- 互补松弛性定理是关于最优原解和对偶解的一个重要结果。
- 我们先假设原问题是一个规范max问题,有着变量 x 1 . . . . x n x_1....x_n x1....xn且 m ≤ c o n s t r a i n t s m\leq constraints m≤constraints
- 让 s 1 . . . , s m s_1...,s_m s1...,sm成为原问题的slack
- 然后对偶问题的 y 1 , . . . y m y_1,...y_m y1,...ym且 n ≥ c o n s t r a i n t s n\geq constraints n≥constraints
- 让 e 1 , e 2 , . . . , e n e_1,e_2,...,e_n e1,e2,...,en成为Surplus。
- 互补松弛性如下图所示:



- 如果一个最优解一直,那么对偶互补性可以决定补问题的解。
- 但你知道 x 1 = 2 , x 2 = 0 , x 3 = 8 x_1=2, x_2 = 0, x_3 = 8 x1=2,x2=0,x3=8的时候,你就知道 e 1 , e 3 = 0 e_1,e_3 = 0 e1,e3=0,所以也可以知道 y 1 = 0 y1 = 0 y1=0。
- 此时你也知道 y 2 , y 3 ≥ 0 y_2,y_3\geq 0 y2,y3≥0。
- 那么你就可以解出DUAL的方程了!
这篇关于挑战运筹学——敏感度分析及对偶性的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





