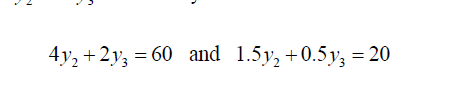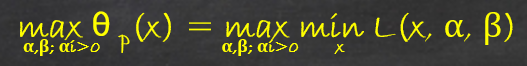Welcome To My Blog 在约束最优化问题(Constrained Optimization)中,常常利用拉格朗日对偶性(Lagrange duality)将原始问题转换为对偶问题,通过求解对偶问题而得到原始问题的解,该方法可用在最大熵模型(Maximum Entropy)和支持向量机(Support Vector Machine). 约束最优化问题 标准形式: f(x),

笔记是听了b站大神的白板推导机器学习系列课，再结合李航老师的《统计学习方法》、周志华老师的西瓜书以及其他优秀博主的博客而成（浑然天成！！！）： https://space.bilibili.com/97068901?from=search&seid=9183191776664110144（大神的白板推导机器学习系列课传送门） 对于大神的课，我只能说太强了，讲的特别特别好！下面让我们开始吧！

影子价格 将问题用数学形式完整地表达 LP问题的一般形式 将数学符号简化 我们将会学习在优化问题中改变 A 0 , C 0 o r B A_0, C_0 or B A0​,C0​orB会导致什么。在很多情况中，constraint同样会变化，所以有关限制的研究也是要考虑的。 考虑一个案例 x 1 x_1 x1​是每周生产士兵玩具的数量。 x 2 x_2 x2​是每周生产火车

0. 内容介绍         在约束最优化问题中， 常常利用拉个朗日对偶性将原始问题转化为对偶问题，通过解对偶问题而得到原始问题的解，该方法应用在很多的统计学习方法中。例如在上一篇文章中（http://blog.csdn.net/robin_xu_shuai/article/details/52791306）所说的最大熵模型。在学习最大熵模型中我们看到，需要求解满足所有已知条件并且使得熵最大的