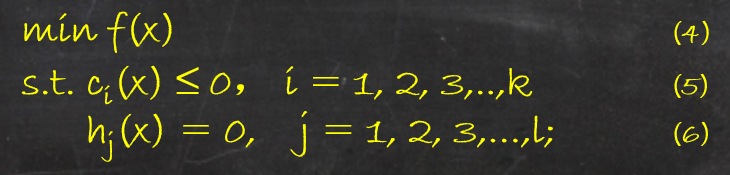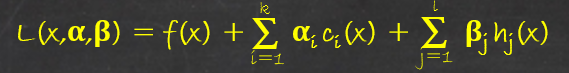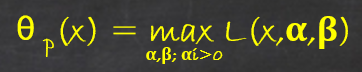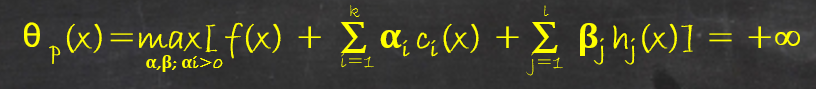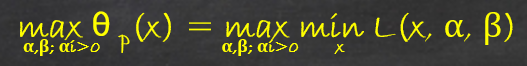本文主要是介绍拉格朗日对偶性问题-《统计学习方法》学习笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
0. 内容介绍
在约束最优化问题中, 常常利用拉个朗日对偶性将原始问题转化为对偶问题,通过解对偶问题而得到原始问题的解,该方法应用在很多的统计学习方法中。例如在上一篇文章中(http://blog.csdn.net/robin_xu_shuai/article/details/52791306)所说的最大熵模型。在学习最大熵模型中我们看到,需要求解满足所有已知条件并且使得熵最大的模型,也就是求解问题带约束的极值问题,其解决方法一般采用拉格朗日对偶原理。下面简单介绍拉格朗日对偶原理。
1.原始问题
约束条件可以分成不等式约束条件和等式约束条件,只有等式约束条件的问题解决方法是直接将等式约束加入原问题构造出拉格朗日函数,然后求导即可。现在考虑带不等式约束和等式约束的极值问题如何构造拉格朗日函数求解。
假设f(x), ci(x), hj(x)是定义在Rn上的连续可微函数,约束最优化问题如下:
称此约束最优化问题为原始问题。
首先,引入拉格朗日函数:
这里\alpha和\beta是拉格朗日乘子。此时我们定义(引入)一个函数,这个函数的目的是建立拉格朗日函数和原始问题中的f(x)的关系。
分析这个定义的函数:此时给定某个x,如果x违反原始问题的约束条件,即如果存在某个i使得c_i(w)>0或者存在某个j使得h_j(w)≠0,那么就有:
(因为如果某个i使得约束ci(x)>0, 则可以令αi取正无穷, 如果某个j使得hj(x)≠0, 则可以令βj取正无穷, 而将其他的剩余的拉格朗日乘子取0.)。而相反,如果x满足原问题的约束条件,可得θp(x) =f(x),因此得到:
(这样就将原来的约束问题变成了现在的无约束问题)
所以当我们现在考虑以下的极小化问题时就与原始的最优化问题(4)(5)(6)是等价的.有相同的解。
2.对偶问题
再引入一个公式,将其定义为α, β的函数:
这样将拉格朗日函数转化为了两个参数的函数,并考虑在此基础上的极大化:
我们把这个问题称为原始问题的对偶问题。和原始问题对比只是交换了最大化和最小化的次序,但是解却不一定是相同的,在满足一定的条件下,原始问题和对偶问题的解相同。
这篇关于拉格朗日对偶性问题-《统计学习方法》学习笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!