耶鲁大学 博弈论(Game Theory) 笔记5-纳什均衡之坏风气与银行挤兑

耶鲁大学 博弈论(Game Theory) 笔记5-纳什均衡之坏风气与银行挤兑

纳什均衡

纳什均衡(NE-Nash Equilibrium)定义

策略组合是一个合集，其包含每个参与人的一个已选策略($s_1^{\ast },s_2^{\ast },\dots ,s_M^{\ast }$)。纳什均衡是满足下列条件的策略组合，对于此集合内的参与人$I$，其选择的策略$s_i^{\ast }$是其他参与者所选策略$s_i^{\ast }$的最佳对策。

动机1：不后悔

假设一个纳什均衡，如果将其他人的策略看成不变量，任意参与人$I$都不会改变策略，即任何参与人都严格不会改变策略。其他参与人不改变行为的前提下，自身改变行为并没有好处。

动机2：纳什均衡可以被想象成自我实施的信念。

简单的双人博弈

$B{R}_1(l)=MB{R}_2(U)=l$
$B{R}_1(m)=UB{R}_2(M)=m$
$B{R}_1(r)=DB{R}_2(D)=r$

因此$NE=(D,r)$,它是参与人1的 BR，同时也是参与人 2的BR。

$B{R}_1(l)=MB{R}_2(U)=m$
$B{R}_1(m)=MB{R}_2(M)=m$
$B{R}_1(r)=DB{R}_2(D)=l$

因此$NE=(M,m)$,它是参与人1的 BR，同时也是参与人 2的BR。

纳什均衡与优劣的关系

这个博弈中a为优势策略，同时$NE=(a,a)$。
严格劣势永远不是最优反应，最优反应才可以出现 NE。

弱劣势与弱优势

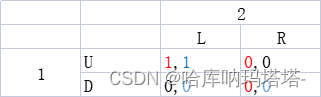
此时存在两个纳什均衡，$NE=(U,L)；NE=(D,R)$。

投资博弈

存在多个投资方，可选投资 10$ 或0$。
$$\begin{gathered} 不投资0\$\to 收益0\$ \\ 投资10\$\to 收益\{\begin{array}{r}5\$,参与投资人数\ge 90\%\\ -10\$,参与投资人数\le 90\%\end{array} \end{gathered}$$
这个博弈存在两个纳什均衡，即所有参与者都投资或者不都不投资。

动机3：博弈会朝着趋向于一个均衡的方向自然发展

较劣的不投资均衡相当于较优的NE处于帕累托劣势(在任何一个人的收益不受损的情况下，至少使一个以上的人收益提高)，在较优均衡中，参与人的收益严格优于较劣均衡中的收益。
这是一个协作博弈(coordination game),之所以能达成在于他不同于囚徒困境，它没有去说服人们采取一个严格劣势策略。

P6
第6集 纳什均衡之约会游戏与古诺模型